B. Drazil and His Happy Friends

B. Drazil and His Happy Friends

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Drazil has many friends. Some of them are happy and some of them are unhappy. Drazil wants to make all his friends become happy. So he invented the following plan.

There are n boys and m girls among his friends. Let's number them from 0 to n - 1 and 0 to m - 1 separately. In i-th day, Drazil invites 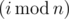-th boy and 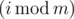-th girl to have dinner together (as Drazil is programmer, i starts from 0). If one of those two people is happy, the other one will also become happy. Otherwise, those two people remain in their states. Once a person becomes happy (or if he/she was happy originally), he stays happy forever.

Drazil wants to know whether he can use this plan to make all his friends become happy at some moment.

Input

The first line contains two integer n and m (1 ≤ n, m ≤ 100).

The second line contains integer b (0 ≤ b ≤ n), denoting the number of happy boys among friends of Drazil, and then follow b distinct integers x₁, x₂, ..., x_b (0 ≤ x_i < n), denoting the list of indices of happy boys.

The third line conatins integer g (0 ≤ g ≤ m), denoting the number of happy girls among friends of Drazil, and then follow g distinct integers y₁, y₂, ... , y_g (0 ≤ y_j < m), denoting the list of indices of happy girls.

It is guaranteed that there is at least one person that is unhappy among his friends.

Output

If Drazil can make all his friends become happy by this plan, print "Yes". Otherwise, print "No".

Sample test(s)

input

2 3 0 1 0

output

Yes

input

2 4 1 0 1 2

output

No

input

2 3 1 0 1 1

output

Yes

Note

By 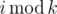 we define the remainder of integer division of i by k.

In first sample case:

• On the 0-th day, Drazil invites 0-th boy and 0-th girl. Because 0-th girl is happy at the beginning, 0-th boy become happy at this day.
• On the 1-st day, Drazil invites 1-st boy and 1-st girl. They are both unhappy, so nothing changes at this day.
• On the 2-nd day, Drazil invites 0-th boy and 2-nd girl. Because 0-th boy is already happy he makes 2-nd girl become happy at this day.
• On the 3-rd day, Drazil invites 1-st boy and 0-th girl. 0-th girl is happy, so she makes 1-st boy happy.
• On the 4-th day, Drazil invites 0-th boy and 1-st girl. 0-th boy is happy, so he makes the 1-st girl happy. So, all friends become happy at this moment.

 

题干大意：

Drazil 有很多朋友，他想让他的所有朋友都变得开心起来。

于是他想了一个办法，将他的男女朋友都编号，按照日期除以编号的得到的余数顺序作为邀请朋友的次序，邀请朋友到他家玩。

如果每次来的俩人其中只要有一个人开心，另一个人也会变得开心起来，并且开心是永久的，输入数据，判断他的目标能否达到。

 

 

code：

/*
author : OVRee

time:2015年2月25日20:46:57

*/

#include <iostream>
using namespace std;

int main()
{
    int m, n ,b, g;
    int flag = 1;
    cin >> m >> n  ;
    /*
     int pub; //  求 m ,n的最小公倍数
    for(int i = 1;;i++)
    {

        if(i%m ==0 && i%n ==0)
        {
            pub = i;
            break;
        }
    }
    其实没必要，求出最小公倍数遍历一遍依然无法保证最终结果，因为开心的传递不仅仅是一次；
    当且仅当 m 和 n 的最小公倍数不是他们本身的时候，才能用 pub 作为循环的边界；为了方便下边循环我直接用10000作为边界，
    即使是99 和100 也保证重复的次数足够多
   
    */
    int boy[105] = {0};
    int girl[105]  = {0};
    int ind;   //用来存下标；
    cin >> b;
    for(int i = 0; i < b; i++)
    {
       cin >> ind;
       boy[ind] = 1;
    }
    cin >> g;
    for(int j = 0;j < g; j++)
    {
        cin >> ind;
        girl[ind] = 1;
    }
    for(int i = 0; i < 10000 ;i++) // 用10000作为循环边界
    {
        if( boy[i%m] || girl[i%n])
        {
            boy[i%m] = 1;
            girl[i%n] = 1;
        }
    }
    // 遍历数组 boy 和 girl；如果出现 0 ，表明还有人不开心，计划没有成功
    for(int i = 0;i < m;i++)
    {
        if(boy[i] == 0)
        {
            flag = 0;
            break;
        }

    }
    for(int i = 0;i < n;i++)
    {
        if(girl[i] == 0)
        {
            flag = 0;
            break;
        }

    }
    if(flag)
        cout << "YES";
    else
        cout << "NO";
    return 0;
}
/*
     ^          ^
    / \        / )
   /  |       / /       ^
   |  z ____<  /      /  >
   |           |     /  /
   Y           \    /  /
   |  >     <   |  <  /
  ( O    ^    O  )  | <
   > ________   N  / /
   / ^     /  / \  \\
   \_/    (_/    | / /
    \            /_/ /
    <___/--<____/___/
*/

 

写得比较烂，掩面走人