HPL Study 2
(1)并行程序的逻辑:
2)考虑任务间所需要的通信通道
3)将任务聚合成复合任务
4)将复合任务分配到核上
(2)共享内存编程:
-
路障 ----> 条件变量,互斥量+忙等待(浪费cpu周期,重置),信号量(多个路障产生竞争条件)
-
临界区(更新共享资源的代码段)------>忙等待(标识变量),互斥量,信号量(信号量没有个体拥有权),读写锁
-
共享内存带来的问题:缓存一致性,线程的安全性,多个线程尝试更新一个共享变量的时候会产生问题(竞争条件)
-
线程是否越多越好:否,由于线程的切换和可能导致的二义性。
-
线程和进程:线程是轻量级的进程,由进程派生,共享进程的大部分资源,但拥有独立的程序计数器和函数调用栈
-
局部性原理
-
空间局部性
-
时间局部性
-
-
串行部分决定了加速比的上限
2.矩阵
(1)矩阵的加减乘除
-
矩阵加减
template <class T>
T** add_sub(int n1,int m1,int n2,int m2,T **a,T *bb,int flag){
T c[n1+10][m1+10];
if(n1!=n2||m1!=m2){
cout<<"No Solution";
return 0;
}
for(int i=1;i<=n1;i++)
for(int t=1;t<=m1;t++)
c[i][t]=a[i][t]+b[i][t]*flag;
}-
矩阵乘法
template <class T>
T** mul(int n1,int m1,int n2,int m2,T **a,T **b){
if(m1!=n2){
cout<<"No Solution";
return 0;
}
T c[n1+10][m2+10];
for(int i=1;i<=n1;i++)
for(int t=1;t<=m2;t++)
c[i][t]=0;
for(int i=1;i<=n1;i++)
for(int t=1;t<=m1;t++){
for(int j=1;j<=m2;j++){
c[i][j]+=a[i][t]*b[t][j];
}
}
}-
矩阵除法
template <class T>
T** div(int n1,int m1,int n2,int m2,T **a,T **b){
T e[n1+10][n2+10];
for(int i=1;i<=n2;i++){
for(int t=1;t<=n2;t++){
if(i==t) e[i][t]=1;
else e[i][t]=0;
}
}
//Gauss-Jordan消元法求矩阵的逆
for(int i=1;i<=n2;i++){
int max=i;
for(int t=i+1;t<=n2;t++)
if(fabs(a[t][i])>fabs(a[max][i])) max=t;
if(fabs(a[max][i])<1e-10){
cout<<"No Solution";
return 0;
}
if(i!=max){
swap(a[i],a[max]);
swap(e[i],e[max]);
}
for(int t=1;t<=n2;t++){
if(t!=i){
double flag=a[i][i]/a[t][i];
for(int j=1;j<=n2;j++){
a[t][j]=flag*a[t][j]-a[i][j];
e[t][j]=flag*e[t][j]-e[i][j];
}
}
}
}
for(int i=1;i<=n2;i++){
printf("%.2lf\n",a[i][n2+1]/a[i][i]);
}
return mul(n1,m1,n2,m2,a,e);
}
(2)矩阵乘法优化
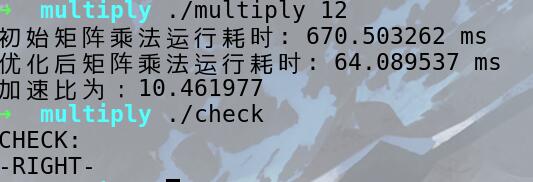
优化方法
-
矩阵分块(减少cache的缺失由于缓存容量的有限性)
-
矩阵的转置(空间局部性原理)
-
指令集向量化:avx256
-
多线程:pthreads
核心代码
`for(int i=1;i<N;i++)
for(int t=1+i;t<N;t++)
swap(b[i][t],b[t][i]);
N--;
thread_count=strtol(argv[1],NULL,10);thread_count=10;
flag=(N+thread_count-1)/thread_count;
pthread_t *threads;
threads=(pthread_t*)malloc(thread_count * sizeof(pthread_t));
for(int i=0;i<thread_count;i++){
int* id = (int*)malloc(sizeof(int));
*id = i;
pthread_create(&threads[i],NULL,matrixMul,(void* )id);
}
for(int i=0;i<thread_count;i++)
pthread_join(threads[i],NULL);
free(threads);`
`void *matrixMul(void *rank){
__m256d a1,b1;
__m256d z= _mm256_setzero_pd();
int my_rank=*((int*)rank);
int T=128;
for(int l=1+flag*my_rank;l<=min(N,flag*(my_rank+1));l+=T)
for(int r=1;r<=N;r+=T)
for(int k=1;k<=N;k+=T)
for(int i=l;i<=min(l+T-1,min(N,flag*(my_rank+1)));i++){
for(int j=r;j<=min(r+T-1,N);j++){
for(int t=k;t<=min(k+T-1,N/4*4);t+=4){
a1=_mm256_loadu_pd(&a[i][t]);
b1=_mm256_loadu_pd(&b[j][t]);
a1=_mm256_mul_pd(a1,b1);
c[i][j]+=a1[3]+a1[2]+a1[1]+a1[0];
}
}
}
for(int i=1+flag*my_rank;i<=min(N,flag*(my_rank+1));i++)
for(int j=1;j<=N;j++){
for(int t=N/4*4+1;t<=N;t++){
c[i][j]+=a[i][t]*b[j][t];
}
}
}`
3.HPL测试
-
查看本机cpu为 12th Gen Intel Core tm i5-12500H 支持的指令集拓展为sse4.1,sse4.2,avx2
AVX2的处理器的单指令的长度是256bit,每颗intelCPU包含2个FMA,一个FMA一个时钟周期可以进行2次乘或者加的运算,那么这个处理器在1个核心1个时钟周期可以执行256bit2FMA2M/A/64=16次浮点运算,也称为16FLOPs,就是Floating Point Operations Per Second
-
查看虚拟机cpu参数主频为3.1GH 8核
-
本机Gfloaps= 8核 * 3.1(GHz) *16=396.8
-
初始实际峰值
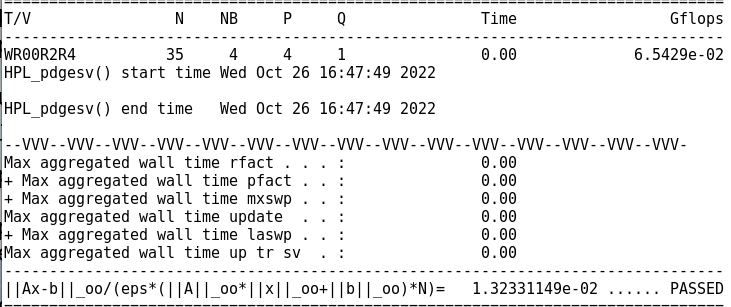
-
调试后实际峰值
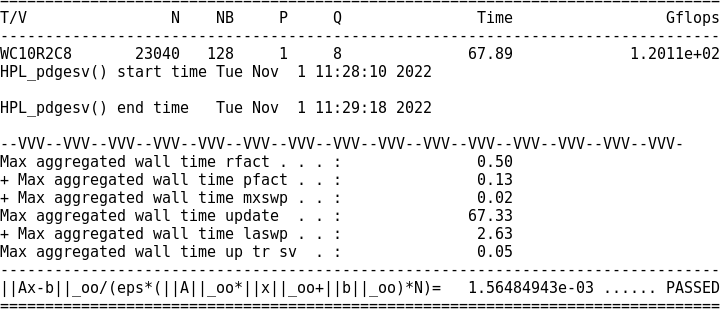
-
调试前比值0.0001769
-
调试后比值0.3026966(和理想差得有点多QAQ)
4.shell
-
对后台CPU使用率的的监控
#!/bin/bash
flag=0
file=/home/consonm/cpuMonitor.txt
echo -e '\t\t\t\tcpu Monitor' >$file
top -b -n 1 | awk 'NR==7,NR==10{print $0}NR==6{print $0}' >> $file
for ((i=4;i<=6;i++))
do
no=`expr $i - 3`
echo "---------------------------------------------------------------------------" >> $file
echo "NO:$no process the first three threads" >> $file
awk -v t=$i 'NR==t{printf $1}' $file | xargs top -H -n 1 -b -p| awk 'NR==7,NR==10{print $0}NR==6{print $0}'>>$file
done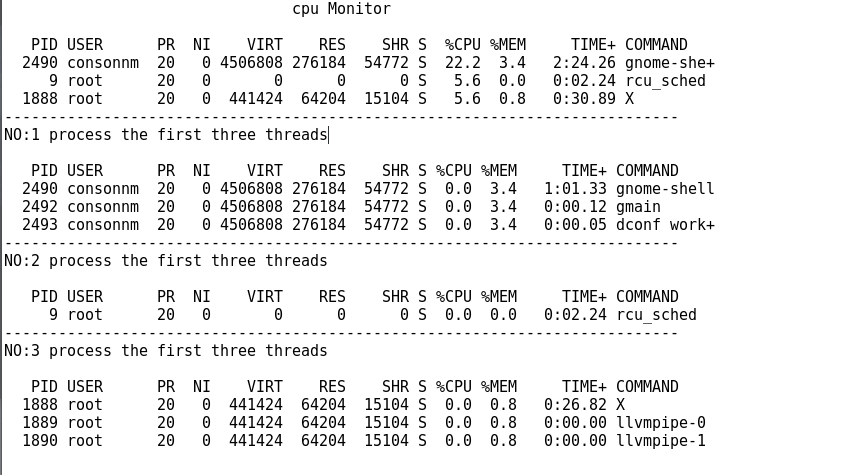
5.结构体数组相加
(1)编译器自动进行内存对齐
-
第一个成员的偏移量为0.
-
每个成员的首地址是自身大小的整数倍
-
结构体的总大小,为其成员中所含最大类型的整数倍。
-
结构体中改变声明变量的顺序可以节约内存
-
内存对齐的意义
-
cpu访问内存的时候,在不同的平台上已2,4,8,16,32字节存取来访问内存,如果对其可能增加访问次数。
-
提高程序在不同平台上的可移植性
-
-
宏声明 (超过结构体中最大成员(类型)的size无效)
-
#pragma pack(n)
-
-
对变量、结构或者联合,设定一个指定大小的对齐格式
-
__attribute__((aligned(n)))
-
(2)指令的使用
-
官方手册
[intel Intrinsics Guide] https://www.laruence.com/sse/#techs=AVX,AVX2 -
注意编译的时候要根据不同的指令加上
CPUID Flags
用几种不同的指令优化了一下似乎差距不大以double型为例
#include <bits/stdc++.h>
#include <pthread.h>
#include <immintrin.h>
#include<omp.h>
using namespace std;
const int N =100;
struct A{
int a;
float b;
double c;
char d;
}a[N+5];
union B{
int a;
float b;
double c;
char d;
}b[N+5];
int main(){
//第一种
__m128i h=_mm_set_epi32(9,6,3,0);
__m128i h1=_mm_set_epi32(3,2,1,0);
for(int i=1;i<=N/4*4;i+=4){
__m256d a1=_mm256_i32gather_pd(&a[i].c,h,8);
__m256d b1=_mm256_i32gather_pd(&b[i].c,h1,8);
a1=_mm256_add_pd(a1,b1);
a[i].c=a1[0],a[i+1].c=a1[1],a[i+2].c=a1[2],a[i+3].c=a1[3];
}
for(int i=N/4*4+1;i<=N;i++)
a[i].c+=b[i].c;
//第二种
for(int i=1;i<=N/4*4;i++){
__attribute__((aligned(32))) double c[4]={a[i].c,a[i+1].c,a[i+2].c,a[i+3].c};
__attribute__((aligned(32))) double d[4]={b[i].c,b[i+1].c,b[i+2].c,b[i+3].c};
__m256d a1=_mm256_load_pd(c);
__m256d b1=_mm256_load_pd(d);
a1=_mm256_add_pd(a1,b1);
a[i].c=a1[0],a[i+1].c=a1[1],a[i+2].c=a1[2],a[i+3].c=a1[3];
}
for(int i=N/4*4+1;i<=N;i++)
a[i].c+=b[i].c;
}
6.Dijkstar算法优化
用堆优化了一下,暂时没想好的并行方法
#include <bits/stdc++.h>
#include <pthread.h>
#include <immintrin.h>
using namespace std;
#define INF 0x3f3f3f3f
#define endl '\n'
typedef long long ll;
int n,m,x,y,v,s,size,head[2000005],flag,dis[2000005],vis[2000005];
struct node{
int to,next,v;
}p[2000006];
struct node1{
int x,v;
}q[2000005];
void add(int x,int y,int v){
p[++flag].to=y;
p[flag].v=v;
p[flag].next=head[x];
head[x]=flag;
}
void push(int x,int v){
q[++size].x=x;
q[size].v=v;
int flag=size;
while((flag>>1)>=1){
int h=flag>>1;
if(q[flag].v<q[h].v){
swap(q[flag],q[h]);
flag=h;
}
else break;
}
}
void pop(){
swap(q[1],q[size--]);
int flag=1;
while((flag<<1)<=size){
int h=flag<<1;
if((h|1)<=size&&q[h].v>q[h|1].v) h=h|1;
if(q[flag].v>q[h].v){
swap(q[flag],q[h]);
flag=h;
}
else break;
}
}
void dijk(){
push(s,0);
while(size){
int x=q[1].x;
pop();
if(vis[x]) continue;
vis[x]=1;
for(int i=head[x];i;i=p[i].next){
if(dis[x]+p[i].v<dis[p[i].to]&&!vis[p[i].to]){
dis[p[i].to]=dis[x]+p[i].v;
push(p[i].to,dis[p[i].to]);
}
}
}
}
int main(int argc,char* argv[]){
cin>>n>>m>>s;
for(int i=1;i<=n;i++)
dis[i]=INF;
dis[s]=0;
for(int i=1;i<=m;i++){
cin>>x>>y>>v;
add(x,y,v);
}
dijk();
for(int i=1;i<=n;i++)
cout<<dis[i]<<" ";
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号