【洛谷P3647】[APIO2014]连珠线

传送门

前言

对于换根的理解应该和其他题解不一样，求过。

题解

首先分析题目简化题意：给定一棵树，从里面选出若干个“三连点”的边，使边权和最大。其中“三连边”有如下图两种形态：\(3-1-2\) 和 \(3-5-6\)

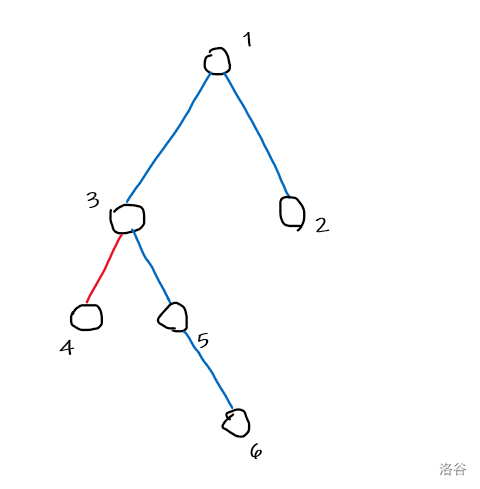
（图源：tommymio）
一开始我想到一种 DP：\(dp(u,0/1/2)\) 表示 \(u\) 节点的子树内可以向下延伸的边数为 \(0/1/2\) 时的最大值，希望通过类似容斥解决形如 \(3-1-2\) 的情况，但实际不太可行（也可能只是我没做出来）。
换一种思路，\(dp(u,0/1)\) 表示 \(u\) 是/不是蓝线中点时，子树内答案的最大值。

• 如果 \(u\) 不是中点，那对于一个儿子 \(v\)，\(v\) 可以是中点也可以不是中点，就有转移式：\(dp(u,0)=\max\{dp(v,1)+w,dp(v,0)\}\)
• 如果 \(u\) 是中点，其实是对于它的一个儿子，\(u\) 是中点，进行“\(u\) 是中点”的转移，即 \(dp(v,0)+w\)；但是对于其他儿子 \(u\) 依旧不是中点，所以转移同上。综合一下就是 \(dp(u,1)=dp(u,0)+\max\{dp(v,0)+w-\max\{dp(v,1)+w,dp(v,0)\}\}\)。

换根！

但是这样做只考虑了竖着的“三连点”，可以发现通过不断换根的位置，可以使树里所有 \(3-1-2\) 形态的选法都变成竖着的。
不能枚举根，所以考虑换根。
记录 \(up(u,0/1)\) 表示 \(u\) 是/不是蓝线中点时，子树外答案的最大值。（换根 DP 都这么设，我这里的子树外是指刨去子树的其他部分）。
先看图：

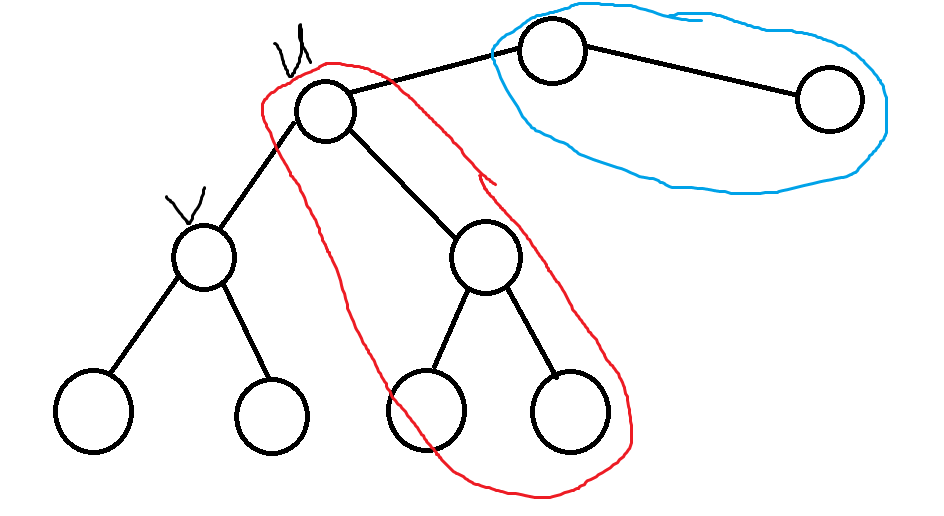
考虑当前从点 \(u\) 向下走到儿子 \(v\)，更新 \(up(v,0/1)\)，显然是从红色部分和蓝色部分来更新。其中蓝色部分是和 \(up(u)\) 有关，红色部分是和 \(dp(u),dp(v)\) 有关。

• 对于红色部分，相当于从 \(dp(u)\) 里撤销 \(v\) 子树的贡献，根据前面的转移可以发现贡献是 \(dp(u,0)-\max\{dp(v,0),dp(v,1)+w\}\)。注意这里先用 \(u\) 不是中点的情况转移，因为 \(u\) 是中点的情况只是相当于多选了一个儿子与他相连（换根相当于此时把 \(v\) 看成根）。
  现在考虑加上 \(u\) 是中点的情况，此时应该从红色部分里面选出当初转移加上的 \(\max\{dp(v,0)+w-\max\{dp(v,1)+w,dp(v,0)\}\}\)，然而此时子树 \(v\) 已经被删掉，所以最大值可能不存在，所以在第一个 DFS 转移时应该同时记录转移加上的最大值和次大值，同时原来的父亲 \(u\) 也可以向 \(v\) 进行中点的连边转移，而这个贡献是 \(up(u,1)-up(u,0)\)。
• 对于蓝色部分，比较简单，贡献就是 \(up(u,0)+trans\)。其中 \(trans\) 为转移变量。具体地，看下面的总转移式。

总转移式（太复杂就贴在代码块里了）：

up[v][0]=dp[u][0]-max(dp[u][0],dp[u][1]+w)+up[u][0]+max(0ll,trans+w);
up[v][1]=dp[u][0]-max(dp[u][0],dp[u][1]+w)+up[u][0]+w;

稍微解释一下为什么可以都从 \(u\) 不作为中点（即第二维为 \(0\)）的情况转移，因为 \(\max\{0,trans+w\}>0\) 就意味着从 \(up(u,1)\) 或者x一个其他的儿子 \(v\) 的 \(dp(v,1)\) 转移过来。
最后有一点细节要注意，对于叶子节点作为中点的情况初始化赋值成极小值，表示不合法方案。

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
const int INF = 0x3f3f3f3f,N = 2e5+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
int n,ecnt=-1,head[N]; 
inline void init()
{
	memset(head,-1,sizeof(head));
	ecnt=-1;
}
struct edge
{
	int nxt,to,w;
}a[N<<1];
inline void add_edge(const int x,const int y,const int w)
{
	a[++ecnt]=(edge){head[x],y,w};
	head[x]=ecnt;
}
int dp[N][2],up[N][2];
int f[N][2],hson[N];
void dfs1(const int u,const int fa)
{
	int maxn=-2e9,cnt_son=0;
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(v==fa) continue; 
		cnt_son++;
		dfs1(v,u);
		int tmp=max(dp[v][0],dp[v][1]+a[i].w);
		int trans=dp[v][0]+a[i].w-max(dp[v][0],dp[v][1]+a[i].w);
		dp[u][0]+=tmp;
		if(maxn<trans)
		{
			f[u][1]=maxn;
			hson[u]=v;
			maxn=trans;
		}
		else f[u][1]=max(f[u][1],trans);
	}
	dp[u][1]=dp[u][0]+maxn;
	if(!cnt_son) dp[u][1]=-2e9;//特判叶子为不合法 
	f[u][0]=maxn;//由于这里的赋值，maxn要初始化成-INF而不能是0，用来表示这种转移不合法 
}
void dfs2(const int u,const int fa)
{
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(v==fa) continue;
		int trans=up[u][1]-up[u][0];//trans是什么意思？下面为什么取max？ 
		//A:相当于多了一个父亲连边的情况，和原来儿子连边的情况取max，为下面转移做准备 
		if(hson[u]==v) trans=max(trans,f[u][1]);
		else trans=max(trans,f[u][0]);
		
		int tmp=max(dp[v][0],dp[v][1]+a[i].w);
		
		up[v][0]=dp[u][0]-tmp+up[u][0]+max(0ll,trans+a[i].w);
		up[v][1]=dp[u][0]-tmp+up[u][0]+a[i].w;
		dfs2(v,u);
	}
}
signed main()
{
	memset(head,-1,sizeof(head));
	n=read();
	for(int i=1;i<n;i++)
	{
		int u=read(),v=read(),w=read();
		add_edge(u,v,w),add_edge(v,u,w);
	}
	dfs1(1,-1); 
	up[1][0]=0,up[1][1]=-2e9;//特判叶子为不合法 
	dfs2(1,-1);
	int ans=0;
	for(int i=1;i<=n;i++)	
		ans=max(ans,max(dp[i][0]+up[i][0],dp[i][1]+up[i][1]));
	printf("%lld\n",ans);
	return 0;
}