【ybtoj】【质数和约数】质数距离

题意

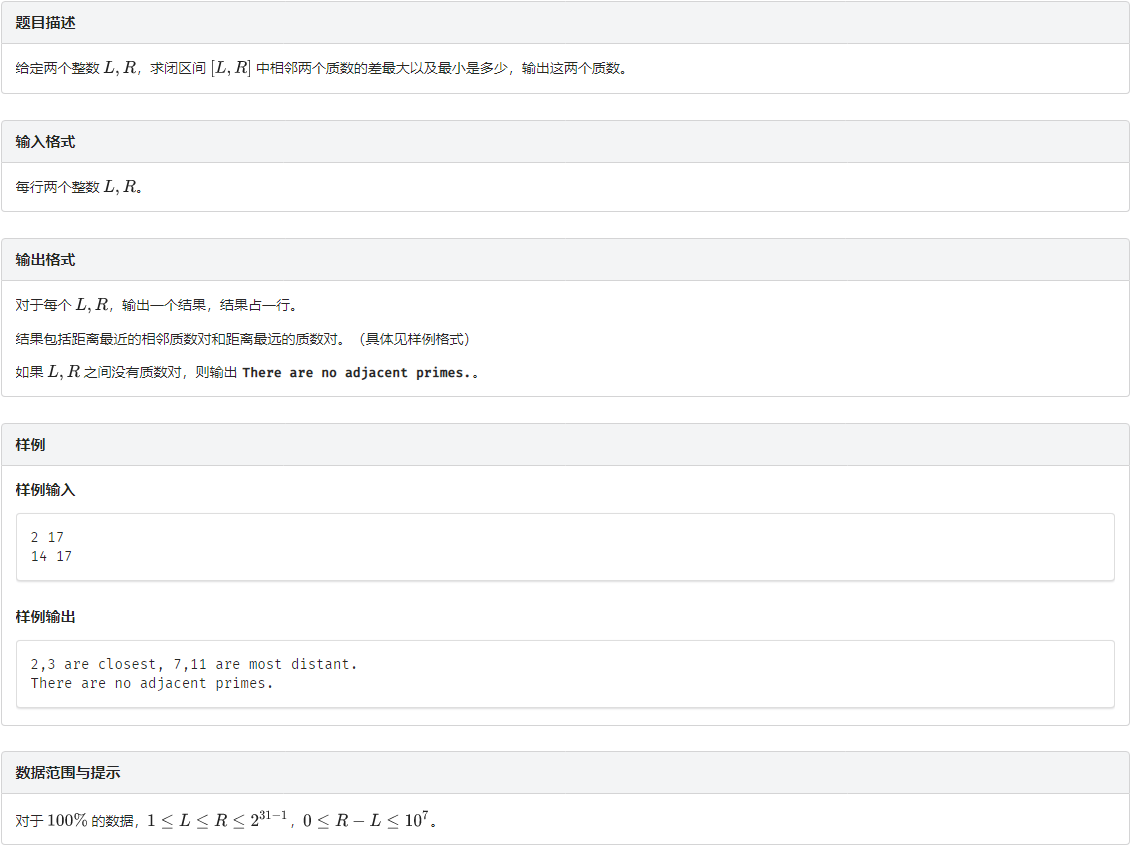
题解

肯定和质数筛法有关，但是 \(l,r\) 都很大所以另辟蹊径。
这里有一个常用的切入点：\(l,r\) 之间的距离很小，所以考虑将区间整体左移 \(l\) 位，这样数组可以存下。
对于任何一个合数 \(n\) ，都有一个不超过 \(\sqrt{n}\) 的约数，用 \(j\times prime_i\) 筛掉 \([l,r]\) 区间内的素数。（\(\lceil l \rceil \le i \le r\) )
如此，复杂度已经降到 \(O(n+\log n\sqrt{n})\) .

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 1e6+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
const int n = 1e6;
bool vis[N],v[N];
int pri[N],cnt;
ll tmp[N];
int l,r;
void deal_prime()
{
	for(int i=2;i<=n;i++)	
	{
		if(!vis[i]) pri[++cnt]=i;
		for(int j=1;j<=cnt&&i*pri[j]<=n;j++) 
		{
			vis[i*pri[j]]=1;
			if(i%pri[j]==0) break;
		}
	}
}
ll max1,max2,min1,min2;
void solve(int l,int r)
{
	memset(v,0,sizeof(v));
	memset(tmp,0,sizeof(tmp));
	int tcnt=0;
	if(l==1) l++;//特判 
	for(int i=1;i<=cnt;i++)
		for(int j=ceil(1.0*l/pri[i]);j<=r/pri[i];j++) 
		{
			if(j==1) continue;
			v[j*pri[i]-l]=1;
		}
	for(ll i=l;i<=r;i++)
		if(!v[i-l]) tmp[++tcnt]=i;
	if(tcnt<2) {printf("There are no adjacent primes.\n");return;}
	max1=min1=tmp[1],max2=min2=tmp[2];
	for(int i=3;i<=tcnt;i++) 
	{
		if(tmp[i]-tmp[i-1]>max2-max1) max2=tmp[i],max1=tmp[i-1];
		if(tmp[i]-tmp[i-1]<min2-min1) min2=tmp[i],min1=tmp[i-1];
	}
	printf("%lld,%lld are closest, %lld,%lld are most distant.\n",min1,min2,max1,max2);
	return;
}
int main()
{
	deal_prime();
	while(scanf("%d%d",&l,&r)!=EOF) solve(l,r);
	return 0;
}