【ybtoj】【DFS】骑士精神

题意

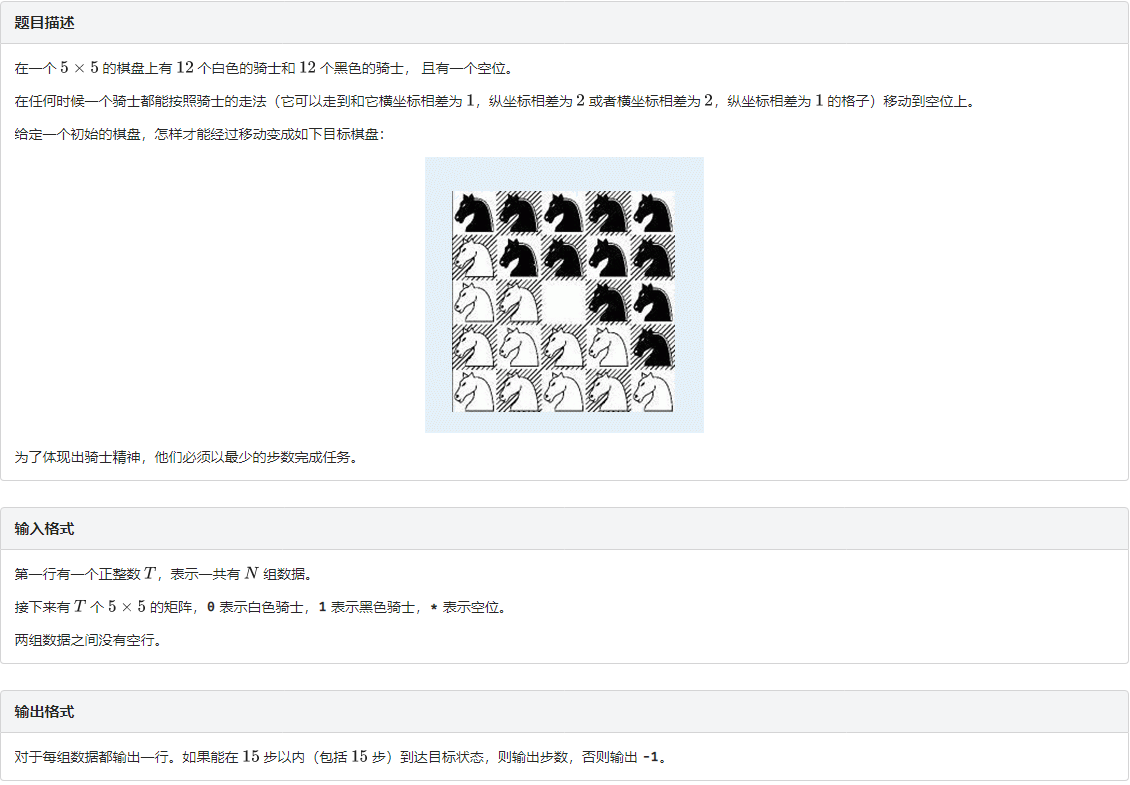
题解

迭代加深搜索，听起来是很高级的东西，实际还挺简单的。
首先正常暴搜复杂度是 \(O(8^{15})\) ，即每次有八种选择，最多 \(15\) 步。肯定会 TLE 。
迭代加深搜索其实本质就是一种剪枝。
相当于对于当前的状态，简单地估算继续操作最少所需步数，如果估值+当前步数\(>\)步数上限，则直接剪枝。
（PS：注意这里估值函数先用变量存起来，避免多次调用可以减少常数）
说实话，迭代加深搜索的复杂度还真不确定，应该根据估值函数写的好坏有关，具体的说不清楚。（但是能过）
其他的就和普通搜索极其类似了。
做题用时：\(35min\)

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,mod = 10086,N = 1e5+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
const int n=5;
const int goal[7][7] = {{},{0,1,1,1,1,1},{0,0,1,1,1,1},{0,0,0,2,1,1},{0,0,0,0,0,1},{}};
int dx[]={1,1,2,2,-1,-1,-2,-2};
int dy[]={2,-2,1,-1,2,-2,1,-1};
char s[6][6];
int a[6][6],ans;
inline int check()
{
	int ret=0;
	for(int i=1;i<=n;i++) 
		for(int j=1;j<=n;j++)
			if(a[i][j]!=goal[i][j]) ret+=a[i][j]!=2;
	return ret;
}
bool dfs(int stp,int x,int y,int lim)
{
	if(!check()) return 1;
	if(stp+check()>lim) return 0;
	for(int i=0;i<8;i++)
	{
		int tx=x+dx[i],ty=y+dy[i];
		if(tx<1||tx>n||ty<1||ty>n) continue;
		swap(a[tx][ty],a[x][y]);
		if(dfs(stp+1,tx,ty,lim)) return 1;
		swap(a[tx][ty],a[x][y]);
	}
	return 0;
}
int main()
{
	int T=read();
	while(T--)
	{
		int x,y;
		for(int i=1;i<=5;i++)
		{
			scanf("%s",s[i]+1);
			for(int j=1;j<=5;j++) 
				if(s[i][j]>='0'&&s[i][j]<='9') a[i][j]=s[i][j]-'0';
				else a[i][j]=2,x=i,y=j;
		}
		bool flag=0;
		for(int i=0;i<=15;i++) 
			if(dfs(0,x,y,i)) {printf("%d\n",i),flag=1;break;}
		if(!flag) printf("-1\n");
	}
	return 0;
}