【ybtoj】【字典树】lowbit求和

题意

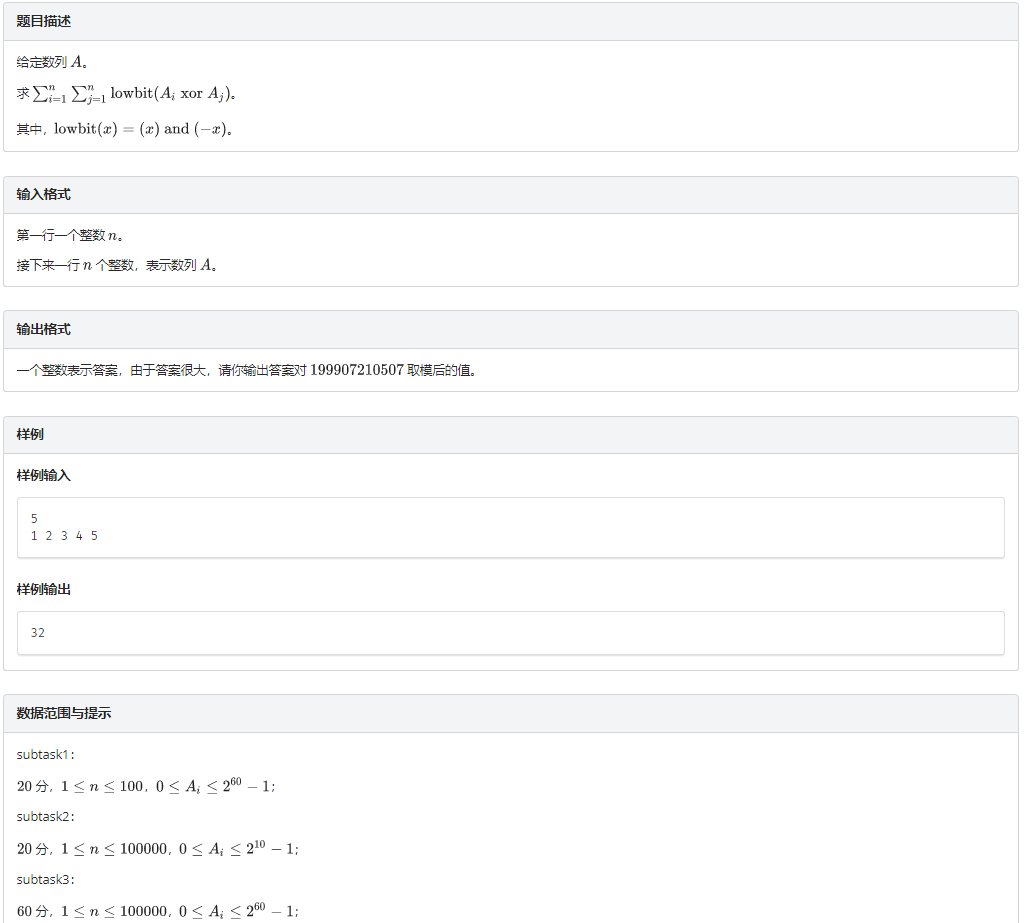
题解

首先考虑 lowbit 有什么特性。
lowbit(x)表示 \(x\) 的二进制最低位的 \(1\) 的所对应的值。
那么对于两个数的异或，从低到高找到二进制第一位不同的位置即可知道 lowbit 的答案。
所以考虑先把所有数插入 Trie 树中，记录每一个位置的数字有多少个。
统计答案的时候把每一个数在 Trie 树上跑一遍，每次找到 Trie 树上与当前位置不同的一边子树内的答案已经确定（即已经找到那些数最低位的 \(1\))，继续走与当前位置相同的一边子树。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 1e5+10;
const ll mod = 199907210507;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
int n,tot=1;
ll a[N*60],num[N*60],trie[N*60][2]; 
inline void insert(int id)
{
	int p=1;
	for(int i=0;i<=61;i++)
	{
		int ch=(a[id]>>i)&1;
		if(!trie[p][ch]) trie[p][ch]=++tot;
		p=trie[p][ch];
		num[p]++;
	}
}
inline ll lowbit(int id)
{
	int p=1;
	ll ret=0;
	for(int i=0;i<=61;i++) 
	{
		int ch=(a[id]>>i)&1;
		if(trie[p][ch^1]) (ret+=num[trie[p][ch^1]]%mod*(1ll<<i)%mod)%=mod;
		p=trie[p][ch];
	}
	return ret;
}
int main()
{	
	n=read();
	for(int i=1;i<=n;i++) 
	{
		a[i]=read();
		insert(i);
	}
	ll ans=0;
	for(int i=1;i<=n;i++) ans+=lowbit(i),ans%=mod;
	printf("%lld",ans);
	return 0;
}