【ybtoj】【最小生成树】序列破解
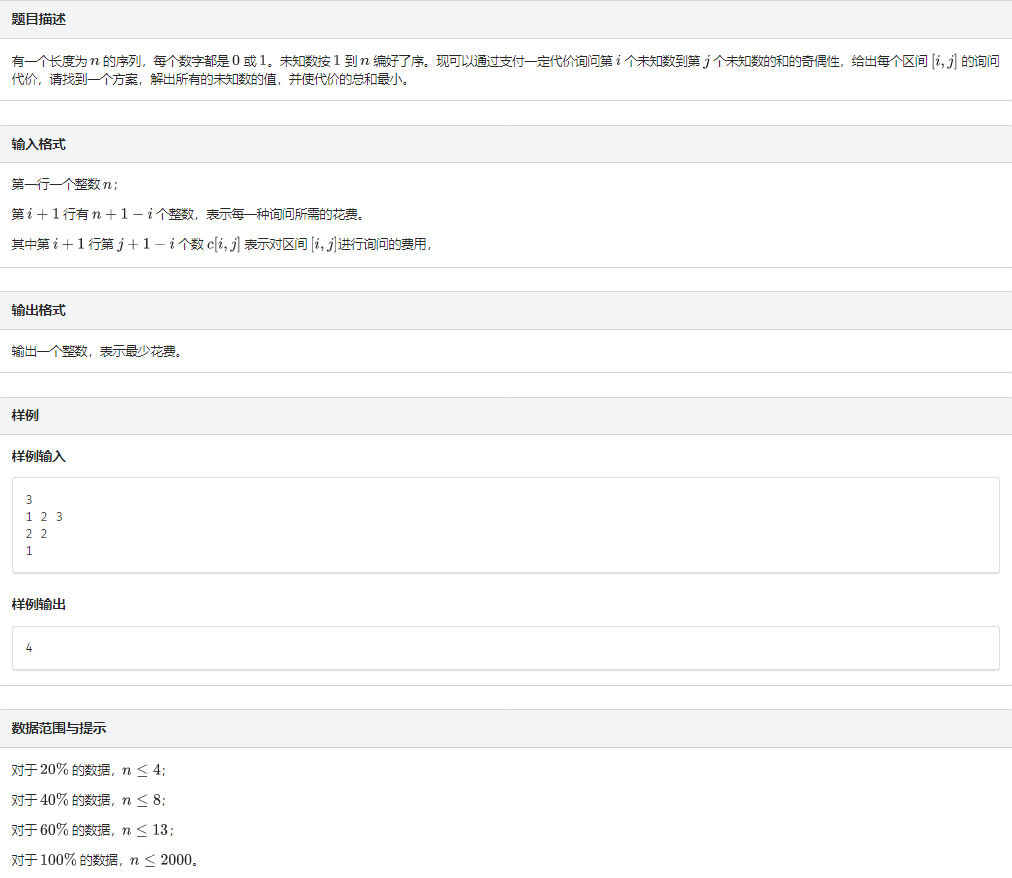
题意
题解
由于奇偶性这种性质比较简单,所以可以考虑一下不同区间的选择对于破解序列有什么影响
很显然,如果 每一个点的前缀和都已知,那么相减即可得出每一个单点的值
而每一个区间 [ L , R ] 可以转化成 sum[R]-sum[L-1]
每一个前缀和已知,就相当于 n 个点的 sum 值都要知道,也就是每一个点都要选择到
同时根据区间的可合并性,就是说 [ L , mid ]+ [ mid+1 , R ]=[ L , R ],相连的点就放到一个集合里,所以是并查集
再看看,这就是 kruskal 最小生成树板子!!!(prim 应该也可以)
关键:区间转化成前缀和相减的形式
代码
序列破解
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 1e5+10;
int n,m,f[N],cnt;
ll ans;
struct edge
{
int x,y;
ll w;
inline bool operator < (const edge oth) const
{
return w<oth.w;
}
}dis[N<<2];
struct point
{
int x,y,z,id;
}a[N];
bool cmp1(point a,point b) {return a.x<b.x;}
bool cmp2(point a,point b) {return a.y<b.y;}
bool cmp3(point a,point b) {return a.z<b.z;}
void init(){for(int i=1;i<=n;i++) f[i]=i;}
int find(int x)
{
if(f[x]==x) return x;
return f[x]=find(f[x]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
a[i].id=i;
}
init();
sort(a+1,a+n+1,cmp1);
for(int i=1;i<n;i++)
dis[++cnt]=(edge){a[i].id,a[i+1].id,(ll)abs(a[i].x-a[i+1].x)};
sort(a+1,a+n+1,cmp2);
for(int i=1;i<n;i++)
dis[++cnt]=(edge){a[i].id,a[i+1].id,(ll)abs(a[i].y-a[i+1].y)};
sort(a+1,a+n+1,cmp3);
for(int i=1;i<n;i++)
dis[++cnt]=(edge){a[i].id,a[i+1].id,(ll)abs(a[i].z-a[i+1].z)};
sort(dis+1,dis+cnt+1);
int ecnt=0;
for(int i=1;i<=cnt;i++)
{
int x=dis[i].x,y=dis[i].y;
if(find(x)!=find(y))
{
f[f[x]]=f[y];
ans+=dis[i].w;
ecnt++;
}
if(ecnt==n-1) break;
}
printf("%lld",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号