微分环节的阶跃响应

from scipy.signal import lti, lsim

# 微分环节的参数
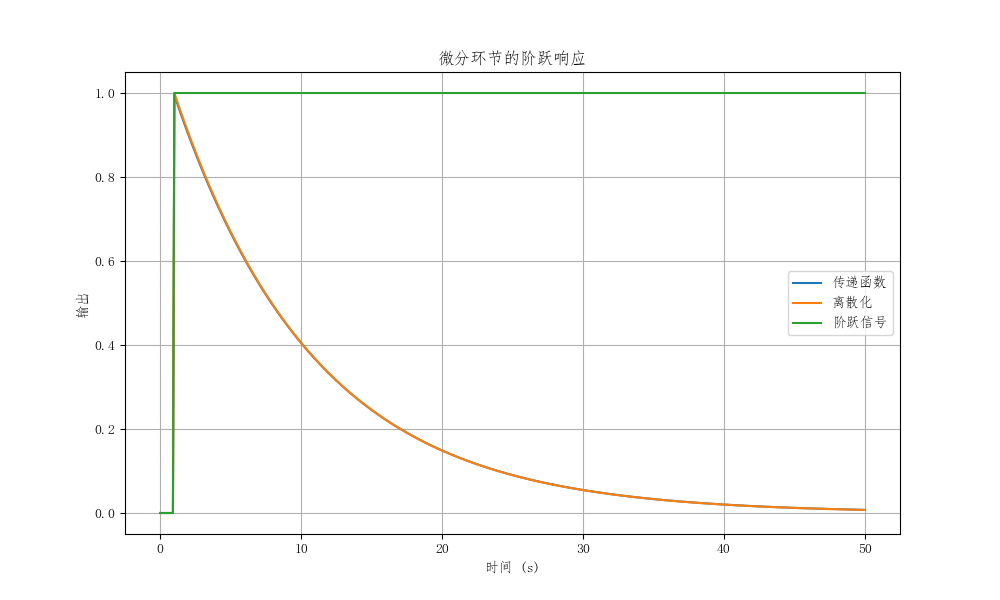
T = 10  # 时间常数

# 创建惯性环节的传递函数
num = [T,0]
den = [T, 1]
system = lti(num, den)

#  10s
#-------
# 10s+1

# 计算阶跃响应
t = np.linspace(0, 50, 500)
dt = 0.1
y = np.zeros(len(t))
y1 = np.zeros(len(t))
out = np.zeros(len(t))
r = np.ones(len(t))
for i in range(len(t)):
	if i < 10:
		r[i] = 0
	else:
		r[i] = 1  
#传递函数
t,y,u = lsim(system, r,t)
# 传递函数离散化
for i in range(1,len(t)):
	out[i] = (1-dt/T)*out[i-1]+(dt/T)*r[i-1]
	y1[i] = r[i]-out[i]

# 绘制阶跃响应曲线
plt.figure(figsize=(10, 6))
plt.plot(t, y,label='传递函数')
plt.plot(t,y1,label='离散化')
plt.plot(t,r,label='阶跃信号')
plt.title('微分环节的阶跃响应')
plt.xlabel('时间 (s)')
plt.ylabel('输出')
plt.legend()
plt.grid(True)
plt.show()