传递函数变换到状态空间
1. 分子为1的传递函数
例：
\[G(s)=\frac{1}{s^3+a_2s^2+a_1s+a_0}
\]
首先写成输入输出关系：
\[(s^3+a_2s^2+a_1s+a_0)Y(s)=U(s)
\]
对应的微分方程：
\[\dddot{y}(t)+a_2\ddot y(t)+a_1\dot y(t)+a_0y(t)=u(t)\\
\dddot{y}(t)=-a_2\ddot y(t)-a_1\dot y(t)-a_0y(t)+u(t)\\
\]
令：
\[x_1=y,\ x_2=\dot y,\ x_3=\ddot y
\]
得到状态空间模型：
\[\begin{array}{l}
\dot x_1=x_2\\
\dot x_2 = x_3\\
\dot x_3 = -a_0x_1-a_1x_2-a_2x_3+u
\end{array}
\Rightarrow
\begin{cases}
\begin{bmatrix}
\dot x_1\\\dot x_2\\\dot x_3
\end{bmatrix}=
\begin{bmatrix}
0&1&0\\0&0&1\\
-a_0&-a_1&-a_2
\end{bmatrix}
\begin{bmatrix}
x_1\\x_2\\x_3
\end{bmatrix}+
\begin{bmatrix}
0\\0\\1
\end{bmatrix}u\\
y=
\begin{bmatrix}
1&0&0
\end{bmatrix}
\begin{bmatrix}
x_1\\x_2\\x_3
\end{bmatrix}
\end{cases}
\]
模拟图：
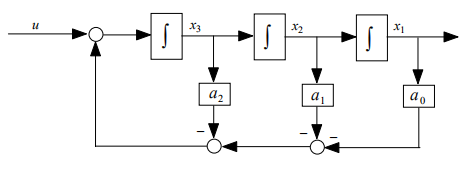
2. 分子不为1的传递函数
例：
\[G(s)=\frac{b_2s^2+b_1s+b_0}{s^3+a_2s^2+a_1s+a_0}=\frac{b(s)}{a(s)}
\]
可以看成：
\[Y(s)=\frac{b(s)}{a(s)}U(s)=b(s)\left [\frac{1}{a(s)}U(s) \right ]=b(s)Y_1(s)
\]
对于
\[Y_1(s)=\frac{1}{a(s)}U(s)
\]
可直接写出
\[G_1(s)=\frac{1}{a(s)}=\frac{1}{s^3+a_2s^2+a_1s+a_0}\\
\Downarrow\\
\begin{cases}
\begin{bmatrix}
\dot x_1\\ \dot x_2\\ \dot x_3
\end{bmatrix}=
\begin{bmatrix}
0&1&0\\0&0&1\\ -a_0&-a_1&-a_2
\end{bmatrix}
\begin{bmatrix}
x_1\\ x_2\\ x_3
\end{bmatrix}+
\begin{bmatrix}
0\\0\\ 1
\end{bmatrix}u\\
y_1=x_1
\end{cases}
\]
对于
\[Y(s)=b(s)Y_1(s)=b(s)X_1(s)=b_2s^2X_1(s)+b_1sX_1(s)+b_0X_1(s)
\]
可得
\[y = b_2\ddot x_1+b_1 \dot x_1 +b_0 x_1\\
y=b_2x_3+b_1x_2+b_0x_1
\]
状态空间模型：
\[\begin{cases}
\begin{bmatrix}
\dot x_1\\ \dot x_2\\ \dot x_3
\end{bmatrix}=
\begin{bmatrix}
0&1&0\\0&0&1\\ -a_0&-a_1&-a_2
\end{bmatrix}
\begin{bmatrix}
x_1\\ x_2\\ x_3
\end{bmatrix}+
\begin{bmatrix}
0\\0\\ 1
\end{bmatrix}u\\
y=\begin{bmatrix}
b_0&b_1&b_2
\end{bmatrix}
\begin{bmatrix}
x_1\\x_2\\x_3
\end{bmatrix}
\end{cases}
\]
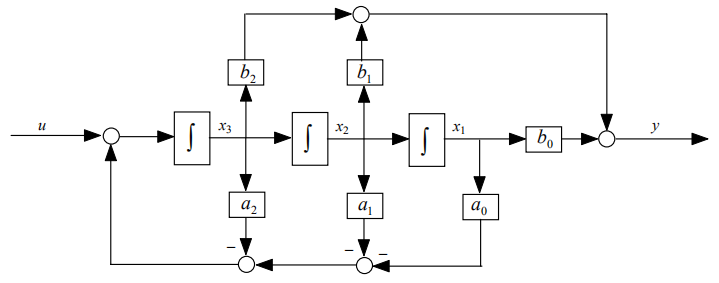
模拟图：
