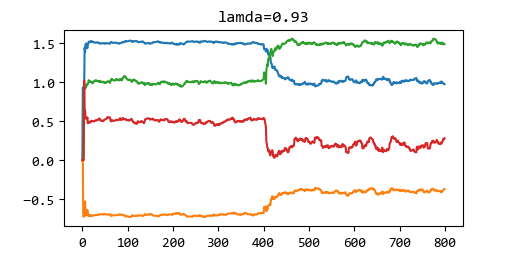
遗忘因子递推最小二乘法FFRLS

import numpy as np 
import matplotlib.pyplot as plt 
from mxulie import M_sequences

if __name__ == '__main__':
	L = 800 #序列长度
	Y = np.zeros(L)
	phi = np.zeros((L,4))
	[M,IM]=M_sequences(L)
	xi = np.sqrt(0.01) * np.random.randn(L,1)
	
	y1 = y2 =0
	u4 = u3 = u2 =u1 =0
	
	P = 1e6 * np.eye(4)
	theta1 = np.zeros((L,4))
	theta1_1 = np.zeros(4)
	lamda = 0.92

	for i in np.arange(L):
		if i <= 400:
			theta = np.array([1.5,-0.7,1,0.5])
		else:
			theta = np.array([1,-0.4,1.5,0.2])


		phi[i,:] = np.array([y1 , y2 ,u3 ,u4])		
		#Y[i] = 1.5*y1 -0.7*y2 + u3 + 0.5*u4 + xi[i]
		Y[i] = np.dot(theta,phi[i,:]) + xi[i]


		# FFRLS       
		K = np.dot(P,phi[i,:])/(lamda+np.dot(np.dot(phi[i,:],P),phi[i,:]))
		theta1[i,:] = theta1_1 + K*(Y[i]-np.dot(phi[i,:],theta1_1))
		P = (1/lamda)*np.dot(np.eye(4)-phi[i,:]*K.reshape((-1,1)),P)




		# 数据更新
		theta1_1 = theta1[i,:]
		y2 = y1
		y1 = Y[i]

		u4 = u3
		u3 = u2
		u2 = u1
		u1 = IM[i]