![]()
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# function that returns dy/dt
def model(y,t):
# u steps from 0 to 2 at t=10
if t<10.0:
u = 0
else:
u = 2
dydt = (-y + u)/5.0
return dydt
# initial condition
y0 = 1
# time points
t = np.linspace(0,40,1000)
# solve ODE
y = odeint(model,y0,t)
# plot results
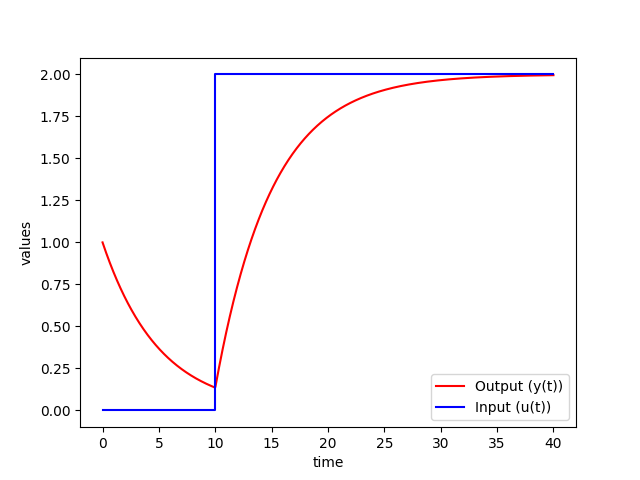
plt.plot(t,y,'r-',label='Output (y(t))')
plt.plot([0,10,10,40],[0,0,2,2],'b-',label='Input (u(t))')
plt.ylabel('values')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()
![]()
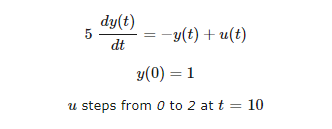


 浙公网安备 33010602011771号
浙公网安备 33010602011771号