机器学习——神经网络

机器学习——神经网络

人工神经网络被用于处理大量输入以及非线性问题。与回归方法不同，回归方法只能处理未知数组成的多项式构成的线性问题，即只能处理简单的关于未知数多项式的非线性问题。而神经网络利用多层网络这一优势，能够处理复杂的非线性问题。

神经网络模型

\(\Theta^{(j)}的维数为s_{j+1} \times (s_j+1)\)

---

分类问题

如上图所示，分类问题分为两种：

• 二分类。二分类只有一个输出。
• 多分类。多分类有K个输出，每个输出如图所示,第i个输出为e_i的形式。

对于这两类分类问题，使用的激励函数为Logistic sigmoid 函数：

\[g(z)=\frac{1}{1+exp(-z)} \]

代价函数

梯度计算

前向传播

基本原理：利用输入的数据，计算下一层的数据，再利用这个数据计算下一层的数据，如此反复，得到最后的输出。

所以，最后结果类似这样:

\[a^{(4)}=g(\Theta^{(3)}g(\Theta^{(2)}g(\Theta^{(1)}x))) \]

后向传播

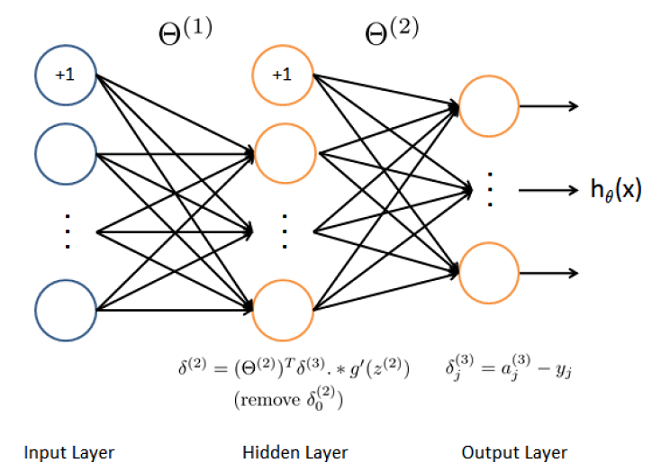
基本原理：利用输出后的误差来估计输出层的前一层误差，再利用这个误差估计更前一层的误差，如此反复，得到各层的误差估计。

根据误差和权值梯度的关系来不断调整权值，进而使得输出后的误差减小到理想值。

基本步骤:

梯度检查

用来检查BP神经网络编程中的小错误。
步骤：

1. 利用后向传播求出梯度D

2. 利用数值方法(差分)求出梯度的近似值GA

3. 比较大小，以确认D,GA近似相等

4. 注释掉GA的计算代码，进行计算

权值初始化

通过计算发现，当权值矩阵\(\Theta\)初始化为全零时，得到的每个隐藏层数据全都相同，使得方法失效。
为了解决这个问题，一般使用随机矩阵初始化各层的权值矩阵\(\Theta\)。

神经网络训练流程

1. 用随机矩阵（向量）初始化权值

2. 利用前向传播求出每个\(x^{(i)}\)的输出\(h_\Theta(x^{(i)})\)

3. 求出代价函数\(J(\Theta)\)

4. 利用后向传播求出\(\frac{\partial}{\partial \Theta_{jk}^{(l)}}J(\Theta)\)

5. 利用梯度检查来检验\(\frac{\partial}{\partial \Theta_{jk}^{(l)}}J(\Theta)\)和数值方法的结果是否相等。完成后，注释掉数值方法代码

6. 利用梯度下降法或者更好的方法，结合后向传播，来最小化\(J(\Theta)\)