© Andrew Kirillov 2006, Conmajia 2012
安德鲁· 基里洛夫 著 , Conmajia 译
作者简介:
安德鲁· 基里洛夫是一名高级软件工程师 。 、 、 。
原文链接: 点击访问
演示 DEMO: 点击下载
源代码: 点击下载
简介 人们在进化计算领域进行了非常多的研究工作 , 。 , 。 , , 。 , —— 甚至是不可能—— 用传统方法来解决这些问题 。 ( , ) 。 要求在给定数量的城市之间找到一条最短的路径 , , , 。 , , 。 , , 。 —— 这些问题往往是不能 ( ) 。
本文讨论了一个用 C#实现的进化计算类库 。 , ( ) 、 ( ) ( ) 。 , 4 个例子进行演示:
该类库的设计思想是保证其灵活性和可重用性 , 。 , , , , 。
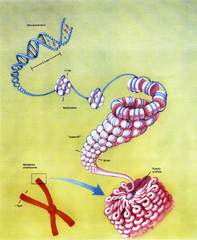
进化计算 遗传算法的历史始于 20 世纪 60 年代 , 在他的工作中首先提出了基于进化的遗传算法 ( ) 。 , , [1] 。 , 。 , , 。
GA 算法基于达尔文关于生物繁殖和遗传的自然选择法则 , ( ) 。 ( ) , 。 染色体是由固定长度的串组成 ( 、 , ) , 。 , 、 、 。
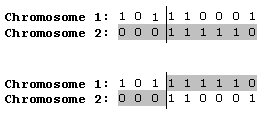
最简单的交叉算子是单点交叉—— 在两个染色体中随机选择一点进行交叉 ( ) :
另一个著名的交叉算子是两点交叉—— 选择染色体中两个随机点 , 。 , , , 算法中还有很多其他的交叉算子 。 , , 。
变异算子处理单一的染色体 , 。 :
如同交叉算子 , 。
所以 , , 算法的每次迭代都包括有以下步骤:
交叉—— 选择随机个体并应用交叉算子
变异—— 选择随机个体并对其应用变异算子
计算每个个体的适合度
选择—— 为下一代选择个体
该算法可能在指定数量的迭代之后 , 。 —— 适合度表示该染色体“好”的程度 。 , , ( —— 译注) 。
有几种选择算子 , 。 Elitism 算法 ( ) —— 选择一定数量的最优染色体进入下一代 。
1992 年 John Koza 提出了一项具有重大意义的新成果—— 遗传编程 ( ) 。 GP 中 , ( ) GA 中那样 , , 。 GP 中被表示成不同大小和形状的解析树 , 。 GP 算法和 GA 算法最主要甚至是唯一的差别之处 。 算法中 , , 、 GA 算法相比 , 。 GP 算法中 , , , 。 —— 染色体互相交换子树 ( 、 ) , 。 , 。
在 GP 算法中计算适合度 , , , 。
2001 年 Candida Ferreira 介绍了另一种被称为基因表达式编程 ( ) [3] 。 。 , , GP 算法一般 。 , 有所不同 。 , GA 算法一样采用固定长度的线性表示 。 , 。 。
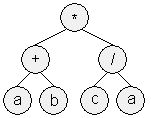
* + / a b c a
染色体表现形式 (a) GP 算法 (b) GEP 算法
上图展示了 GP 算法和 GEP 算法中染色体的不同表现形式 。 —— 算数表达式 (a+b)*(c/a) 。 算法中是以解析树的形式表示的 , GEP 算法则以从左上到右下的顺序线性表示的解析字符串 。 GEP 字符串转换回一颗解析树 , , 。
使用类库 类库基于灵活 、 , 。 , 、 。 、 、 ( ) , 。 , , 、 , 、 , 。 , , IChromosome 接口实现自己的染色体类 , 。 —— 通过实现 ISelectionMethod 和 IFitnessFunction 接口创建自定义选择算法和适合度计算函数 。 , , , 。
为了演示类库的使用方法 , 4 个使用不同进化计算算法的例子:
函数优化 ( )
符号回归计算 ( )
时间序列预测 ( )
旅行商问题 ( )
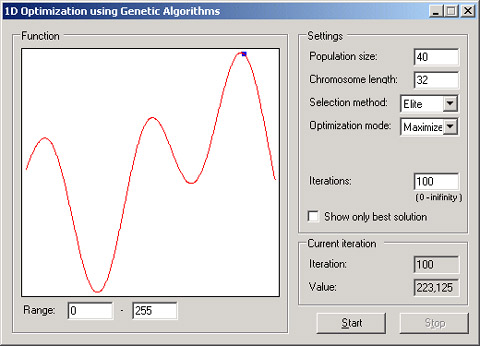
函数优化
函数优化是演示遗传算法的经典问题 。 , , ( —— 译注) , :
1 // 定义优化函数
2 public class UserFunction : OptimizationFunction1D
3 {
4 public UserFunction( ) :
5 base ( new DoubleRange( 0 , 255 ) ) { }
6
7 public override double OptimizationFunction( double x )
8 {
9 return Math.Cos( x / 23 ) * Math.Sin( x / 50 ) + 2 ;
10 }
11 }
12 ...
13 // 创建遗传种群
14 Population population = new Population( 40 ,
15 new BinaryChromosome( 32 ),
16 new UserFunction( ),
17 new EliteSelection( ) );
18 // 运行一代
19 population.RunEpoch( );
上面的例子创建了一个数量为 40 的染色体种群 , 32bit 的二进制串 , 。 ( ) , ( ) , 。 , 。 , 。
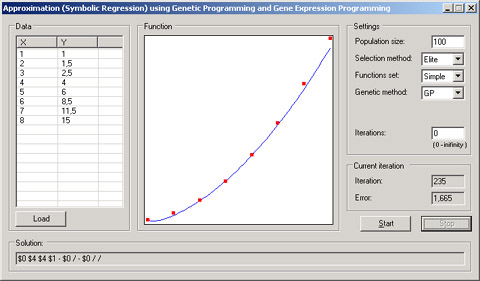
符号回归计算 ( )
符号回归问题的目的是找到针对输入数据的最佳近似函数 。 。 , X 值和一些常数为参数 , Y 值 。
实际解题的代码和上一个例子的代码非常相似 , 。 , , 。 , , GPTreeChromosome 类创建染色体 。 , GEPChromosome 类 。
1 // 需要近似求解的函数(输入数据)
2 double [,] data = new double [5 , 2 ] {
3 {1 , 1 }, {2 , 3 }, {3 , 6 }, {4 , 10 }, {5 , 15 } };
4 // 创建种群
5 Population population = new Population( 100 ,
6 new GPTreeChromosome( new SimpleGeneFunction( 6 ) ),
7 new SymbolicRegressionFitness( data, new double [] { 1 , 2 , 3 , 5 , 7 } ),
8 new EliteSelection( ),
9 0.1 );
10 // 运行一代
11 population.RunEpoch( );
在上面的例子中 , (X,Y) 值对的 。 , Population 类构造函数的最后一个参数—— 该参数的值表示 10% ( 0.1—— 译注) , 90%则为当前代的成员 。
时间序列预测
时间序列预测问题创建了一个基于函数历史值来预测函数未来值的模型 。 , ( ) , 。 。
1 // 需要预测的时间序列
2 double [] data = new double [13 ] { 1 , 2 , 4 , 7 , 11 , 16 , 22 , 29 , 37 , 46 , 56 , 67 , 79 };
3 // 常数
4 double [] constants = new double [10 ] { 1 , 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 };
5 // 滑动窗大小
6 int windowSize = 5 ;
7 // 创建种群
8 Population population = new Population( 100 ,
9 new GPTreeChromosome( new SimpleGeneFunction( windowSize + constants.Length ) ),
10 new TimeSeriesPredictionFitness( data, windowSize, 1 , constants ),
11 new EliteSelection( ) );
12 // 运行一代
13 population.RunEpoch( );
可以看到 , —— 只是修改了适合度计算函数和算法的一些参数 。 , 。
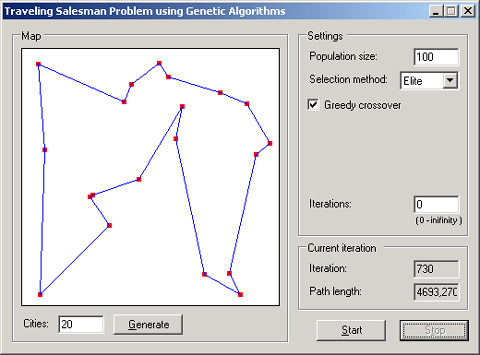
旅行商问题
旅行商问题目标是在城市之间找到一条最短路径 , , , 。 NP 困难问题 。 , , 。 , , 。
1 // 创建种群
2 Population population = new Population( populationSize,
3 new PermutationChromosome( citiesCount ),
4 new TSPFitnessFunction( map ),
5 new EliteSelection( )
6 );
值得注意的是 , , PermutationChromosome 类要求创建新的适合度计算函数 ( TSPFitnessFunction ) 。 。 PermutationChromosome 类可以得到问题解 , 。 TSPChromosome 类 ( ) , 。
多年来 , 。 , , 。 , 世纪 90 年代末 , 。 , 。 ( )
结论 以上的 4 个例子展示了本文类库的最初目标—— 灵活 、 、 , 。 , , , 。 , , 。
参考文献 [1] Ajith Abraham, Nadia Nedjah and Luiza de Macedo Mourelle, Evolutionary Computation: from Genetic Algorithms to Genetic Programming // Genetic Systems Programming: Theory and Experiences, volume 13 of Studies in Computational Intelligence, pages 1-20. Springer, Germany, 2006.
[2] John R. Koza, Genetic Programming // Version 2 – Submitted August 18, 1997 for Encyclopedia of Computer Science and Technology.
[3] Ferreira, Gene Expression Programming: A new adaptive algorithm for solving problems // Complex Systems, Vol. 13, No. 2, pp. 87–129, 2001.
历史 [4.8.2012] - 完成翻译
[2.8.2012] - 开始翻译本文
[16.10.2006] - 发表本文
许可证 本文及其附属的任何源代码和文件均以 GNU General Public License ( ) 许可证发布 。
( )
© Andrew Kirillov 2006, Conmajia 2012


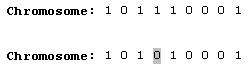
 * + / a b c a
* + / a b c a







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· AI与.NET技术实操系列(二):开始使用ML.NET
· 单线程的Redis速度为什么快?