树结构初识
为什么需要树这种数据结构
1) 数组存储方式的分析
优点:通过下标方式访问元素,速度快。对于有序数组,还可使用二分查找提高检索速度。
缺点:如果要检索具体某个值,或者插入值(按一定顺序)会整体移动,效率较低
2) 链式存储方式的分析
优点:在一定程度上对数组存储方式有优化(比如:插入一个数值节点,只需要将插入节点,链接到链表中即可,
删除效率也很好)。
缺点:在进行检索时,效率仍然较低,比如(检索某个值,需要从头节点开始遍历)
3) 树存储方式的分析
能提高数据存储,读取的效率, 比如利用 二叉排序树(Binary Sort Tree),既可以保证数据的检索速度,同时也
可以保证数据的插入,删除,修改的速度。
树示意图
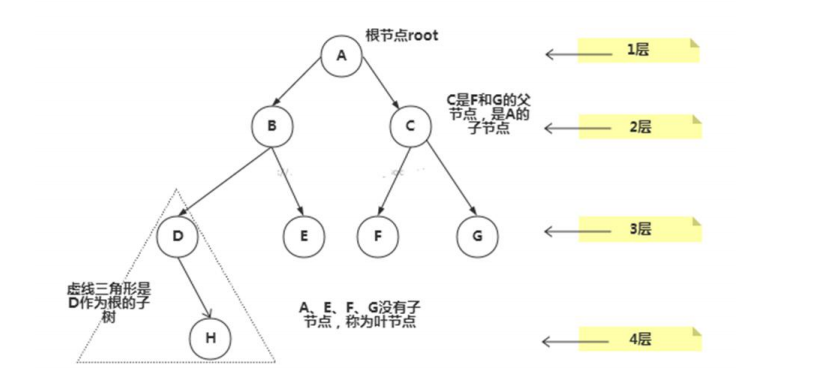
|
树的常用术语(结合示意图理解): 1) 节点 2) 根节点 3) 父节点 4) 子节点 5) 叶子节点 (没有子节点的节点) 6) 节点的权(节点值) 7) 路径(从 root 节点找到该节点的路线) 8) 层 9) 子树 10) 树的高度(最大层数) 11) 森林 :多颗子树构成森林 |
二叉树的概念
1) 树有很多种,每个节点最多只能有两个子节点的一种形式称为二叉树。
2) 二叉树的子节点分为左节点和右节点
3) 示意图
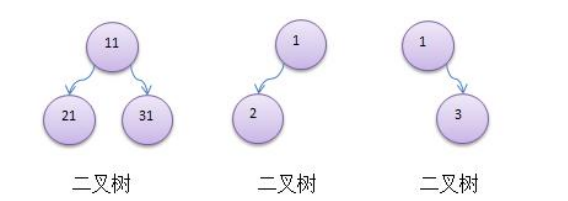
4) 如果该二叉树的所有叶子节点都在最后一层,并且结点总数= 2^n -1 , n 为层数,则我们称为满二叉树。
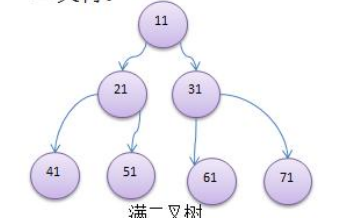
5) 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连续,倒数第二
层的叶子节点在右边连续,我们称为完全二叉树
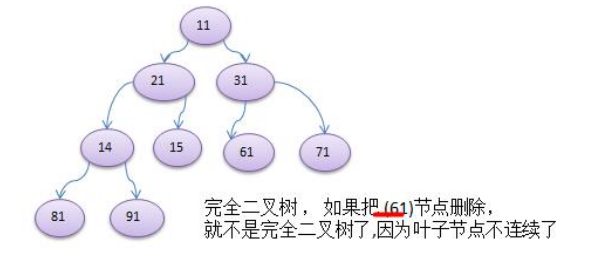
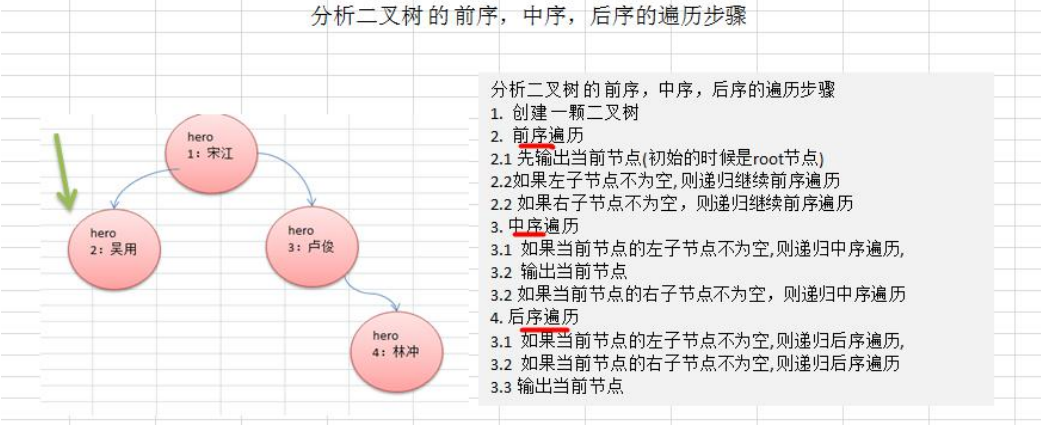
二叉树遍历的说明
1) 前序遍历: 先输出父节点,再遍历左子树和右子树
2) 中序遍历: 先遍历左子树,再输出父节点,再遍历右子树
3) 后序遍历: 先遍历左子树,再遍历右子树,最后输出父节点
4) 小结: 看输出父节点的顺序,就确定是前序,中序还是后序
二叉树遍历应用实例(前序,中序,后序)
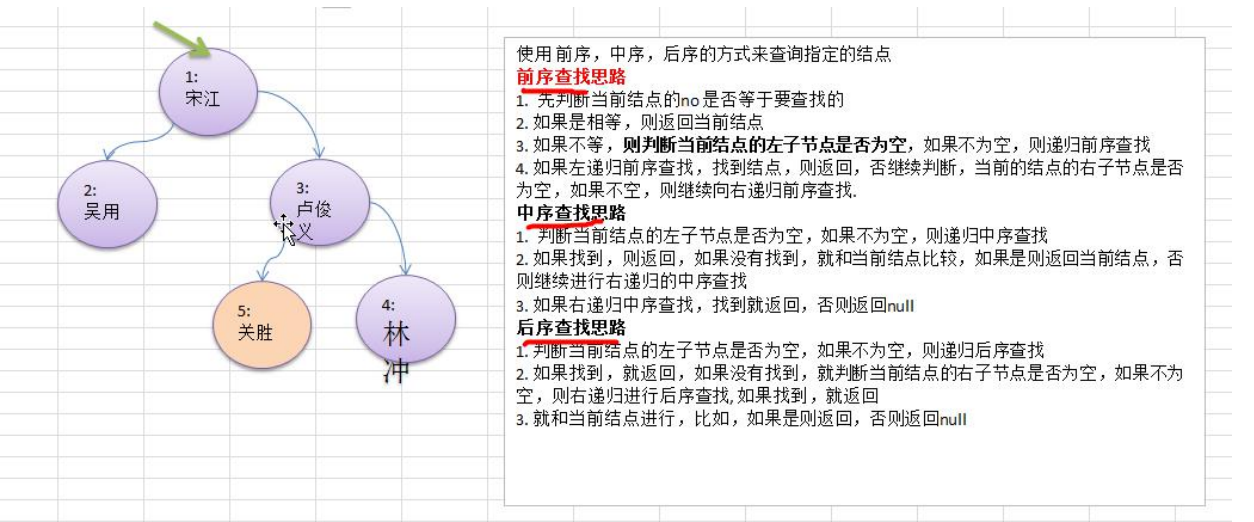
二叉树-查找指定节点
1) 请编写前序查找,中序查找和后序查找的方法。
2) 并分别使用三种查找方式,查找 heroNO = 5 的节点
3) 并分析各种查找方式,分别比较了多少次
4) 思路分析图解
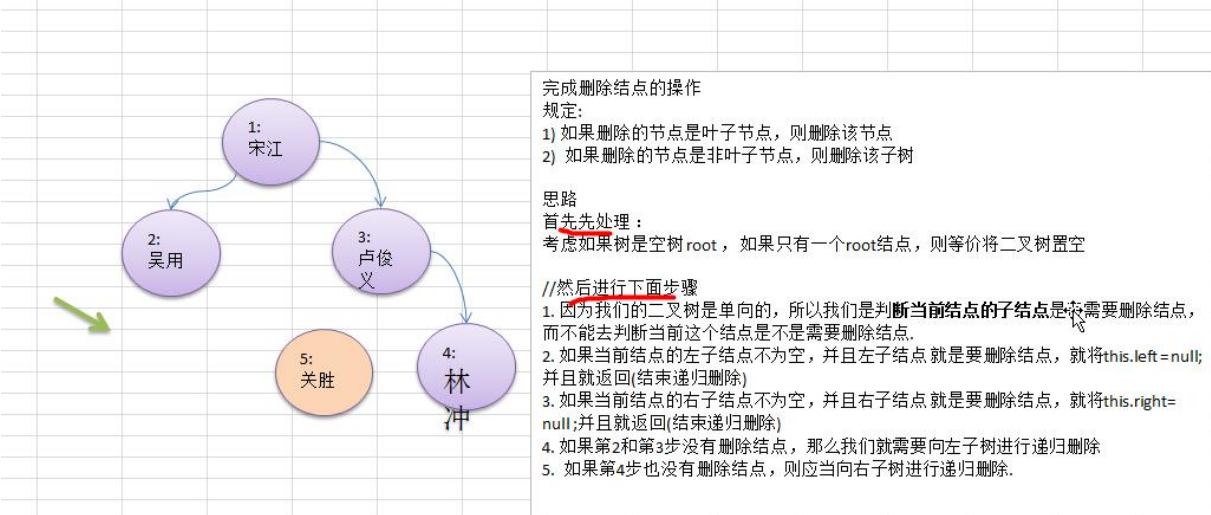
二叉树-删除节点
1) 如果删除的节点是叶子节点,则删除该节点
2) 如果删除的节点是非叶子节点,则删除该子树.
代码实现
public class BinaryTreeDemo {
public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
//说明,我们先手动创建该二叉树,后面我们学习递归的方式创建二叉树
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//测试
// System.out.println("前序遍历"); // 1,2,3,5,4
// binaryTree.preOrder();
//测试
// System.out.println("中序遍历");
// binaryTree.infixOrder(); // 2,1,5,3,4
//
// System.out.println("后序遍历");
// binaryTree.postOrder(); // 2,5,4,3,1
//前序遍历
//前序遍历的次数 :4
// System.out.println("前序遍历方式~~~");
// HeroNode resNode = binaryTree.preOrderSearch(5);
// if (resNode != null) {
// System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
// } else {
// System.out.printf("没有找到 no = %d 的英雄", 5);
// }
//中序遍历查找
//中序遍历3次
// System.out.println("中序遍历方式~~~");
// HeroNode resNode = binaryTree.infixOrderSearch(5);
// if (resNode != null) {
// System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
// } else {
// System.out.printf("没有找到 no = %d 的英雄", 5);
// }
//后序遍历查找
//后序遍历查找的次数 2次
// System.out.println("后序遍历方式~~~");
// HeroNode resNode = binaryTree.postOrderSearch(5);
// if (resNode != null) {
// System.out.printf("找到了,信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
// } else {
// System.out.printf("没有找到 no = %d 的英雄", 5);
// }
//测试一把删除结点
System.out.println("删除前,前序遍历");
binaryTree.preOrder(); // 1,2,3,5,4
binaryTree.delNode(5);
//binaryTree.delNode(3);
System.out.println("删除后,前序遍历");
binaryTree.preOrder(); // 1,2,3,4
}
}
//定义BinaryTree 二叉树
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//删除结点
public void delNode(int no) {
if(root != null) {
//如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if(root.getNo() == no) {
root = null;
} else {
//递归删除
root.delNode(no);
}
}else{
System.out.println("空树,不能删除~");
}
}
//前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//中序遍历
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//前序遍历
public HeroNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//中序遍历
public HeroNode infixOrderSearch(int no) {
if(root != null) {
return root.infixOrderSearch(no);
}else {
return null;
}
}
//后序遍历
public HeroNode postOrderSearch(int no) {
if(root != null) {
return this.root.postOrderSearch(no);
}else {
return null;
}
}
}
//先创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; //默认null
private HeroNode right; //默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
//递归删除结点
//1.如果删除的节点是叶子节点,则删除该节点
//2.如果删除的节点是非叶子节点,则删除该子树
public void delNode(int no) {
//思路
/*
* 1. 因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点.
2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
3. 如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
4. 如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除
5. 如果第4步也没有删除结点,则应当向右子树进行递归删除.
*/
//2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
//3.如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
//4.我们就需要向左子树进行递归删除
if(this.left != null) {
this.left.delNode(no);
}
//5.则应当向右子树进行递归删除
if(this.right != null) {
this.right.delNode(no);
}
}
//编写前序遍历的方法
public void preOrder() {
System.out.println(this); //先输出父结点
//递归向左子树前序遍历
if(this.left != null) {
this.left.preOrder();
}
//递归向右子树前序遍历
if(this.right != null) {
this.right.preOrder();
}
}
//中序遍历
public void infixOrder() {
//递归向左子树中序遍历
if(this.left != null) {
this.left.infixOrder();
}
//输出父结点
System.out.println(this);
//递归向右子树中序遍历
if(this.right != null) {
this.right.infixOrder();
}
}
//后序遍历
public void postOrder() {
if(this.left != null) {
this.left.postOrder();
}
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
//前序遍历查找
/**
*
* @param no 查找no
* @return 如果找到就返回该Node ,如果没有找到返回 null
*/
public HeroNode preOrderSearch(int no) {
System.out.println("进入前序遍历");
//比较当前结点是不是
if(this.no == no) {
return this;
}
//1.则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
//2.如果左递归前序查找,找到结点,则返回
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {//说明我们左子树找到
return resNode;
}
//1.左递归前序查找,找到结点,则返回,否继续判断,
//2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序遍历查找
public HeroNode infixOrderSearch(int no) {
//判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入中序查找");
//如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点
if(this.no == no) {
return this;
}
//否则继续进行右递归的中序查找
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//后序遍历查找
public HeroNode postOrderSearch(int no) {
//判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {//说明在左子树找到
return resNode;
}
//如果左子树没有找到,则向右子树递归进行后序遍历查找
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入后序查找");
//如果左右子树都没有找到,就比较当前结点是不是
if(this.no == no) {
return this;
}
return resNode;
}
}
//



