如何判断链表有环

 前天晚上临睡觉前看到了公众号脚本之家推送的一篇文章，文章内容是一道算法题，并给出了思路解释，但没有具体源码实现，这让我觉得少了点什么，于是，趁周末，我补齐了缺失的内容，好了，no code, no bb，我们开始吧。

题目描述：

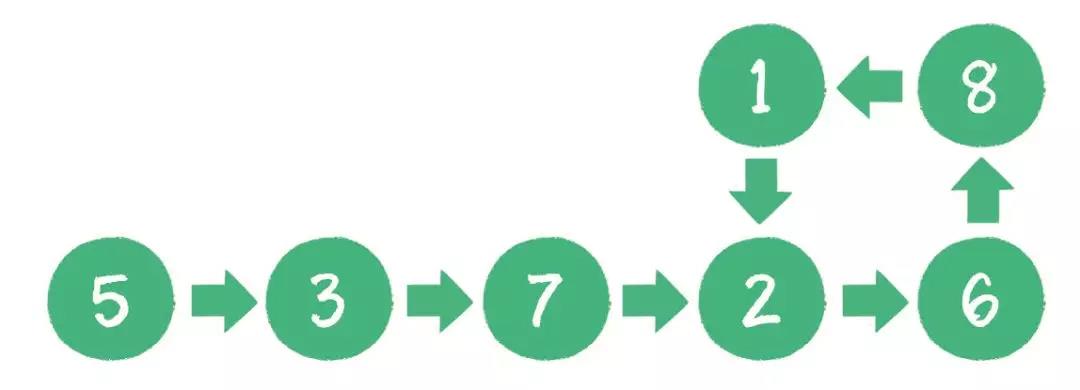
有一个单向链表，链表中有可能出现“环”，就像下图这样。那么，如何用程序来判断该链表是否为有环链表呢？（图片来自公众号）

 

方法1：

从头开始遍历整个单链表，每遍历一个新节点，就把它与之前遍历过的节点进行比较，如果值相同，那么就认为这两个节点是一个节点，则证明链表有环，停止遍历，否则继续遍历下一个节点，重复刚才的操作，直到遍历结束。结合上图来说，流程是这样的：

① 得到 "3"节点，把它与第一个节点 “5”比较，值不相等，继续遍历下一个节点 “7”。（从第二个节点开始遍历）

② 得到 “7”节点，把它依次与 “5”、“3”比较，值不相等，继续遍历下一个节点 “2”

③ 重复以上操作，直到遍历完节点 “1”

④ 得到节点 “2”，把它依次与 “5”、“3”、“7”、“2”、“6”、“8”、“1”进行比较，当比较到节点 “2”时，值相等，遍历结束，证明该链表有环。

假设链表的节点数量为n，则该解法的时间复杂度为O（n2），由于没有创建额外的存储空间，所以空间复杂度为O（1）

链表的实现比较简单，我只写了一个add方法，一个display方法：

//单向链表
public class SingleLinkedList {
    private Node head;//标识头节点
    private int size;//标识链表中节点个数
    
    public SingleLinkedList() {
        this.size = 0;
        this.head = null;
    }
    
    //node类
    private class Node{
        private Object data;//每个节点的数据
        private Node next;//指向下一个节点的链接
        
        public Node(Object data) {
            this.data = data;
        }
    }
    
    /**
     * 将节点插入链表
     * @param data 带插入的值
     */
    public void add(Object data) {
        Node temp = head;
        if (size == 0) {
            head = new Node(data);
            size++;
            return;
        }
        while (temp.next != null) {
            temp = temp.next;
        }
        temp.next = new Node(data);
        size++;
    }
    
    /**
     * 从头开始遍历节点
     */
    public void display() {
        if (size > 0) {
            Node node = head;
            if (size == 1) {
                System.out.println("[" + node.data + "]");
                return;
            }
            while (node != null) {
                System.out.println(node.data);
                node = node.next;
            }
        } else {
            System.out.println("[]");
        }
    }
}

方法1如下：

    /**
     * 根据索引得到链表的某个节点的值
     * @param key
     * @return
     */
    public Object getNode(int key) {
        
        if (key < 0 || key > size - 1) {
            throw new ArrayIndexOutOfBoundsException("越界！");
        } else {
            Node temp = head;
            int count = 0;
            while (temp != null) {
                if (count == key) {
                    return temp.data;
                }
                temp = temp.next;
                count++;
            }
            
        }
        return null;
    }
    
    
    /**
     * 从头开始，依次与给定索引位置的节点的值进行比较，如果相同，则返回true，否则false
     * @param key
     * @return
     */
    public boolean havaSameElement(int key) {
        boolean flag = false;
        int count = 0;
        Node temp = head;
        while (temp != null && count < key) {
            if (temp.data == getNode(key)) {
                flag = true;
                return flag;
            }
            count++;
            temp = temp.next;
        }
        return flag;
        
    }
    
    /**
     * 方式1
     * @return
     */
    public boolean isAnnulate1() {
        boolean flag = false;
        for (int i = 1; i < size; i++) {
            if (havaSameElement(i)) {
                flag = true;
                break;
            }
        }
        return flag;
    }

方法2：

这种方法用到了HashSet中add方法去重的特点，思路是这样的：

① new一个HashSet，用来存储之前遍历过的节点值

②从头节点head开始，依次遍历链表中的节点，并把它add到集合中

③ 如果在集合中已经有一个相同的值，那么会返回false，这样便证明链表有环，退出遍历

方法2如下：

    /**
     * 方式2
     * @return
     */
    public boolean isAnnulate2() {
        boolean flag = false;
        Set<Object> set = new HashSet<>();
        Node temp = head;
        while (temp != null) {
            if (!set.add(temp.data)) {
                flag = true;
                break;
            }
            temp = temp.next;
        }
        return flag;

    }

 

方法3：

定义两个指针tortoise与rabbit，让它们一开始均指向head头节点，之后，tortoise每次向后移动一个节点，rabbit每次向后移动2个节点，只要这个链表是有环的，它们必定会在某一次移动完后相遇，什么？你问我为什么？我们来思考这样一个问题，两个人在运动场跑步，他们的起始位置都是一样的，当开跑后，只有在两种情况下，他们的位置会重合，第一就是他们的速度始终一致，第二就是跑得快的那个人套圈，如下图所示：

 

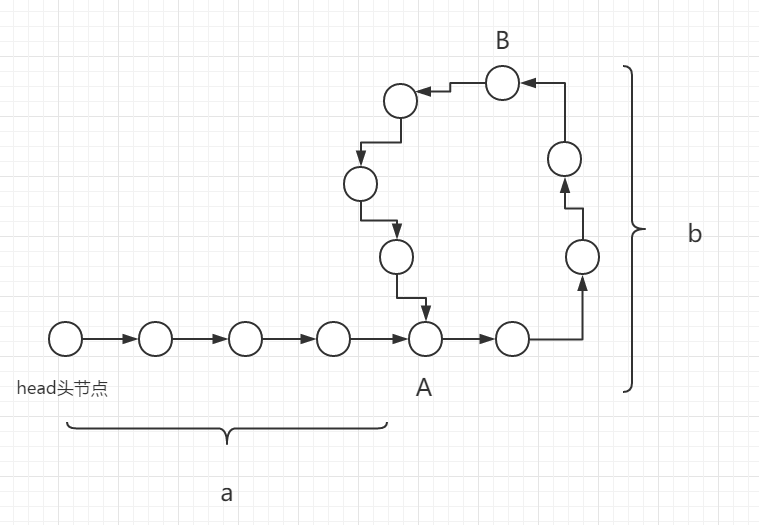
我们假设两位跑步的同学速度始终不变，即tortoise以V的速度进行移动，rabbit以2V的速度进行移动，在经过了相同的时间T后，他们相遇了，此时tortoise移动的距离为VT，而rabbit移动的距离为2VT，他们移动的距离差VT，即为这个链表中 “环”的周长，如上图所示，节点A表示为环入口，节点B表示他们第一次相遇，我们将head头节点至节点A的距离记为a，将节点A至他们第一次相遇的节点B的距离记为b，通过我们刚才的分析，不难得出，tortoise移动的距离VT = a + b，等量代换，他们移动的距离差也为 a+ b，所以链表中环的周长为 a + b，现在已知节点A至节点B的距离为b，那么节点B至节点A的距离便为a，至此，发现什么了？head头节点到节点A的距离同样为a，我们建立一个指针 start 指向头节点，它与B节点处的tortoise同时以一个节点的速度进行移动，一段时间后，它们将在环入口相遇。我们不光能证明一个链表是否有环，还能找到环的入口。

方法3如下：

    public Node getIntersect() {
        Node temp = head;
        Node tortoise = temp;
        Node rabbit = temp;
        while (rabbit != null && rabbit.next != null) {
            tortoise = tortoise.next;
            rabbit = rabbit.next.next;
            if (tortoise == rabbit) {
                return tortoise;
            }
        }
        return null;
    }
    
    public Object isAnnulate3() {
        Node temp = head;
        if (temp == null) {
            return null;
        }
        Node intersect = getIntersect();
        if (intersect == null) {
            return null;
        }
        Node startNode = head;
        while (startNode != intersect) {
            startNode = startNode.next;
            intersect = intersect.next;
        }
        return startNode.data;
        
    }

我要说明的是，方法3中的代码只是 “伪代码”，它并不能真的证明链表有环，并返回环的入口节点值。至于为什么，我的理解是，因为单链表的结构特点，它并不会真的存在 “环”，我们这里说的环只是把它抽象出来，实际上，单链表中一个节点只保留有对它后面那个节点的引用，并没有对它前面节点的引用，所以，并不存在真正的 “环”，不过，这种思路还是值得学习的。假设链表的节点数量为n，则该算法的时间复杂度为O（n），除指针外，没有占用任何额外的存储空间，所以空间复杂度为O（1）。

完整代码如下：

package judgeLinkedListCircle;

import java.util.HashSet;
import java.util.Set;


/**
 * 单向链表
 * @author Cone
 * @since 2019年7月27日
 *
 */
public class SingleLinkedList {
    private Node head;//标识头节点
    private int size;//标识链表中节点个数
    
    public SingleLinkedList() {
        this.size = 0;
        this.head = null;
    }
    
    //node类
    private class Node{
        private Object data;//每个节点的数据
        private Node next;//指向下一个节点的链接
        
        public Node(Object data) {
            this.data = data;
        }
    }
    
    /**
     * 将节点插入链表
     * @param data 带插入的值
     */
    public void add(Object data) {
        Node temp = head;
        if (size == 0) {
            head = new Node(data);
            size++;
            return;
        }
        while (temp.next != null) {
            temp = temp.next;
        }
        temp.next = new Node(data);
        size++;
    }
    
    /**
     * 从头开始遍历节点
     */
    public void display() {
        if (size > 0) {
            Node node = head;
            if (size == 1) {
                System.out.println("[" + node.data + "]");
                return;
            }
            while (node != null) {
                System.out.println(node.data);
                node = node.next;
            }
        } else {
            System.out.println("[]");
        }
    }
    
    /**
     * 根据索引得到链表的某个节点的值
     * @param key
     * @return
     */
    public Object getNode(int key) {
        
        if (key < 0 || key > size - 1) {
            throw new ArrayIndexOutOfBoundsException("越界！");
        } else {
            Node temp = head;
            int count = 0;
            while (temp != null) {
                if (count == key) {
                    return temp.data;
                }
                temp = temp.next;
                count++;
            }
            
        }
        return null;
    }
    
    
    /**
     * 从头开始，依次与给定索引位置的节点的值进行比较，如果相同，则返回true，否则false
     * @param key
     * @return
     */
    public boolean havaSameElement(int key) {
        boolean flag = false;
        int count = 0;
        Node temp = head;
        while (temp != null && count < key) {
            if (temp.data == getNode(key)) {
                flag = true;
                return flag;
            }
            count++;
            temp = temp.next;
        }
        return flag;
        
    }
    
    /**
     * 方式1
     * @return
     */
    public boolean isAnnulate1() {
        boolean flag = false;
        for (int i = 1; i < size; i++) {
            if (havaSameElement(i)) {
                flag = true;
                break;
            }
        }
        return flag;
    }
    
    
    /**
     * 方式2
     * @return
     */
    public boolean isAnnulate2() {
        boolean flag = false;
        Set<Object> set = new HashSet<>();
        Node temp = head;
        while (temp != null) {
            if (!set.add(temp.data)) {
                flag = true;
                break;
            }
            temp = temp.next;
        }
        return flag;

    }
    
    public Node getIntersect() {
        Node temp = head;
        Node tortoise = temp;
        Node rabbit = temp;
        while (rabbit != null && rabbit.next != null) {
            tortoise = tortoise.next;
            rabbit = rabbit.next.next;
            if (tortoise == rabbit) {
                return tortoise;
            }
        }
        return null;
    }
    
    /**
     * 方式3
     * @return
     */
    public Object isAnnulate3() {
        Node temp = head;
        if (temp == null) {
            return null;
        }
        Node intersect = getIntersect();
        if (intersect == null) {
            return null;
        }
        Node startNode = head;
        while (startNode != intersect) {
            startNode = startNode.next;
            intersect = intersect.next;
        }
        return startNode.data;
        
    }

}

如有错误，欢迎指正。

代码已上传至github：

https://github.com/Thinker-Mars/ByteDance