POJ 2653 Pick-up sticks <<判断线段交

题意

求与上方的线段都没有交集的线段

思路

暴力判断线段交即可。

判断线段交的方法：

1.快速排斥实验

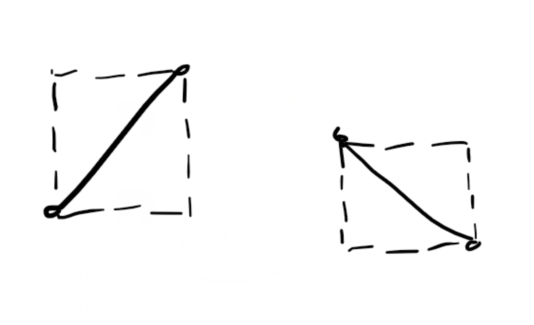
如图，如果两条线段不相交，他们所组成的矩形也不相交，而判断矩形相交是很方便的，用这个方法可以快速筛掉一些线段。

当然这并不是充要条件，两矩形相交也可能线段不相交。

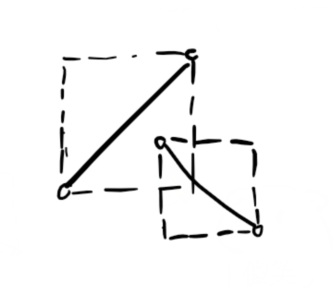
所以矩形不相交是线段不相交的充分非必要条件。

2.那么正常的判断线段交方法：向量叉积，也就是跨立实验

线段相交，也就是说线段$P_1P_2$跨过了线段$Q_1Q_2$，同样，$Q_1Q_2$跨过了$P_1P_2$，所以有$(\overrightarrow{P_1P_2}\times\overrightarrow{P_1Q_1})\cdot (\overrightarrow{P_1P_2}\times\overrightarrow{P_1Q_2})<=0$使得$Q_1Q_2$跨过了$P_1P_2$

同理，有$(\overrightarrow{Q_1Q_2}\times\overrightarrow{Q_1P_1})\cdot (\overrightarrow{Q_1Q_2}\times\overrightarrow{Q_1P_2})<=0$使得$P_1P_2$跨过了$Q_1Q_2$

代码

#include<algorithm>
#include<cstdio>
using namespace std;
const int maxn=1e5+7;
const double eps=1e-8;
struct Point{
    double x,y;
};
struct Segment{
    Point a,b;
}seg[maxn];
double cross(Point p,Point a,Point b)
{
    //cout<<p.x<<","<<p.y<<";"<<a.x<<","<<a.y<<";"<<b.x<<","<<b.y<<endl;
    Point pa={a.x-p.x,a.y-p.y};
    Point pb={b.x-p.x,b.y-p.y};
    double ret=pa.x*pb.y-pa.y*pb.x;
    //cout<<ret<<endl;
    return ret;
}
bool intersect(Segment l1,Segment l2)
{
    return 
        max(l1.a.x,l1.b.x) >= min(l2.a.x,l2.b.x) &&
        max(l2.a.x,l2.b.x) >= min(l1.a.x,l1.b.x) &&
        max(l1.a.y,l1.b.y) >= min(l2.a.y,l2.b.y) &&
        max(l2.a.y,l2.b.y) >= min(l1.a.y,l1.b.y) &&
        cross(l1.a,l2.a,l1.b)*cross(l1.a,l2.b,l1.b) <= 0 &&
        cross(l2.a,l1.a,l2.b)*cross(l2.a,l1.b,l2.b) <= 0;
}
int main()
{
    int n;
    while(~scanf("%d",&n)&&n)
    {
        for(int i=0;i<n;i++)
        {
            scanf("%lf%lf%lf%lf",&seg[i].a.x,&seg[i].a.y,&seg[i].b.x,&seg[i].b.y);
        }
        printf("Top sticks:");
        for(int i=0;i<n-1;i++)
        {
            for(int j=i+1;j<n;j++)
            {
                if(intersect(seg[i],seg[j]))
                    goto next;
            }
            printf(" %d,",i+1);
            next:;
        }
        printf(" %d.\n",n);

    }
}