【GCC编译器】计算支配树信息 Part1 - 求CFG的深度为主搜索树

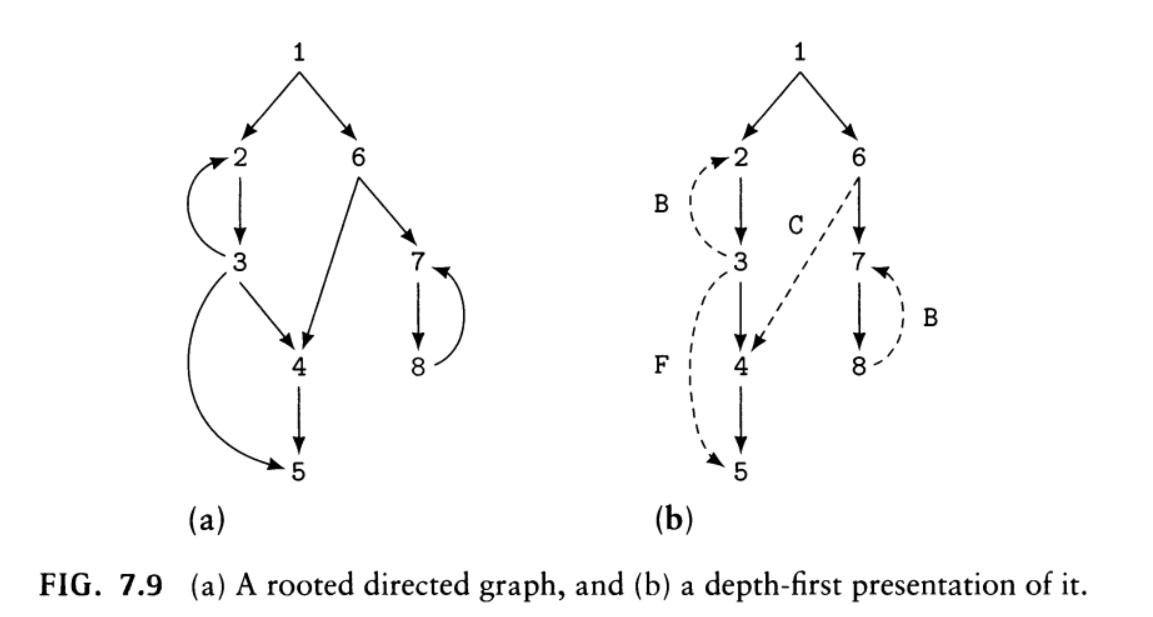
• 深度为主生成树：将图中所有的结点和那些构成深度为主次序的边表示为树的形式，并将其他的边(这些边不是深度为主次序的一部分)用一种有别于树的方式来表示(我们用虚线而不是实线表示它们)
  • 属于深度为主生成树的边称为树边（tree edge）
  • 不属于深度为主生成树的那些边分为三类:
    • 前向边（forward edge）：从一个结点到一个直接后裔并且不是树边的边（用F标识），主编号由小到大
    • 后向边（back edge）：从一个结点到树中它的一个祖先的边（用B标识），主编号由大到小
    • 横向边（cross edge）：连接两个在树中互不是祖先的结点的边（用C标识），主编号由大到小

 

• GCC在计算深度为主搜索树时，使用的是非递归算法。利用stack先入后出的特点，完成树的深度优先遍历。为了使得代码逻辑更清晰，删除了CDI_POST_DOMINATORS模式相关的代码。
•  遍历过程中一共生成3张映射表：
  • bb的index --> bb的深度为主编号：保存在映射表m_dfs_order
  • bb的深度为主编号 --> bb的index：保存在映射表m_dfs_to_bb
  • bb的深度为主编号 --> 在深度为主生成树中，bb的父节点的深度为主编号：保存在m_dfs_parent

/* The nonrecursive variant of creating a DFS tree.  BB is the starting basic
   block for this tree and m_reverse is true, if predecessors should be visited
   instead of successors of a node.  After this is done all nodes reachable
   from BB were visited, have assigned their dfs number and are linked together
   to form a tree.  */

void
dom_info::calc_dfs_tree_nonrec (basic_block bb)
{
  edge_iterator *stack = new edge_iterator[m_n_basic_blocks + 1];
  int sp = 0;
  unsigned d_i = dom_convert_dir_to_idx (CDI_DOMINATORS);

  /* Initialize the first edge.  */
  edge_iterator ei = ei_start (bb->succs);

  /* When the stack is empty we break out of this loop.  */
  while (1)
    {
      basic_block bn;
      edge_iterator einext;

      /* This loop traverses edges e in depth first manner, and fills the
         stack.  */
      while (!ei_end_p (ei))
        {
          edge e = ei_edge (ei);

	      /* Deduce from E the current and the next block (BB and BN), and the
	         next edge.  */
          bb = e->src;
          bn = e->dest;
          /* 三种情况下跳过当前节点：
             1. BN是end block，对于CDI_DOMINATORS模式来说，即exit block.
             2. 没有给BN分配保存dominance information的空间.
             3. 已经被访问过的节点. */
          if (bn == m_end_block || bn->dom[d_i] == NULL
              || m_dfs_order[bn->index])
            {
              ei_next (&ei);
              continue;
            }

          /* 深度优先，遍历BN的后继节点. */
          einext = ei_start (bn->succs);
          
          gcc_assert (bn != m_start_block);
	      /* Fill the DFS tree info calculatable _before_ recursing.  */
          /* my_i    是BB的深度为主编号.
             child_i 是BN的深度为主编号. */
          TBB my_i;
          if (bb != m_start_block)
            my_i = m_dfs_order[bb->index];
          else
            my_i = *m_dfs_last;
          /* 将BN和child_i的映射关系存入表m_dfs_order. */
          TBB child_i = m_dfs_order[bn->index] = m_dfsnum++;
          /* 将child_i和BN的映射关系存入表m_dfs_to_bb. */
          m_dfs_to_bb[child_i] = bn;
          /* 将BB和BN的父子节点关系写入表m_dfs_parent. */
          m_dfs_parent[child_i] = my_i;

	      /* Save the current point in the CFG on the stack, and recurse.  */
          stack[sp++] = ei;
          ei = einext;
        }

      if (!sp)
        break;
      ei = stack[--sp];

      /* OK.  The edge-list was exhausted, meaning normally we would
         end the recursion.  After returning from the recursive call,
         there were (may be) other statements which were run after a
         child node was completely considered by DFS.  Here is the
         point to do it in the non-recursive variant.
         E.g. The block just completed is in e->dest for forward DFS,
         the block not yet completed (the parent of the one above)
         in e->src.  This could be used e.g. for computing the number of
         descendants or the tree depth.  */
      ei_next (&ei);
    }
  delete[] stack;
}