HashMap原理
结构
数组+链表 结构 ;
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next; //同buket上下一个节点
}
transient Node<K,V>[] table; //初始化是个null,第一次put时候才有值
hash算法
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); //>>>无符号右移
}
key的hash值, 高16位 和低16位异或操作, 这样比较均匀分散位置 ;
put操作图

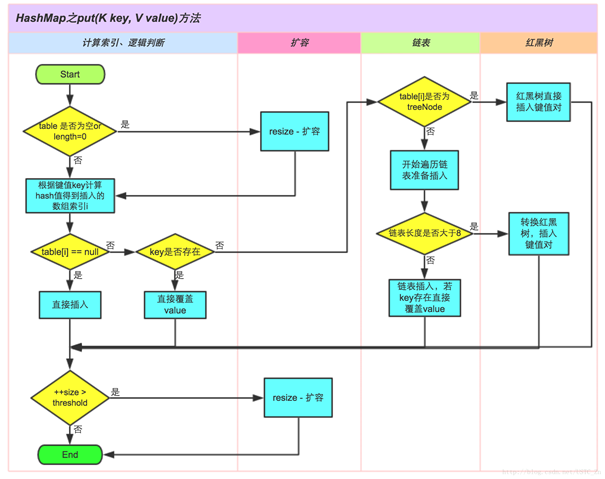
get 操作图
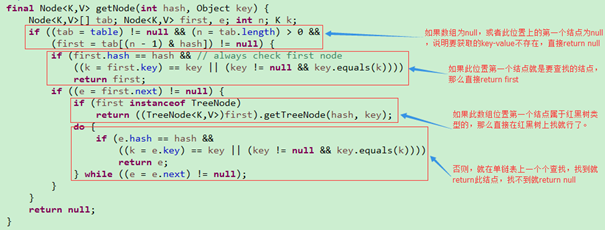
如果节点是红黑树, 则根据hash值 大小,分别从root节点,左右边查找, 红黑树特性 左边hash值 <右边, 一直往下找即可;
resize扩容
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab; // 超过最大值,不在扩容
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // 否则扩大为原来的 2 倍
}
else if (oldThr > 0) /// 初始化时,threshold 暂时保存 initialCapacity 参数的值
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) { // 计算新的 resize 上限
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) { // 将旧的键值对移动到新的哈希桶数组中
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null) // 无链条
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode) // 拆红黑树,先拆成两个子链表,再分别按需转成红黑树
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // 拆链表,拆成两个子链表并保持原有顺序
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) { // 原位置不变的子链表
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else { // 原位置偏移 oldCap 的子链表( 原索引+oldCap)
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// 放到新的哈希桶中(// 原索引放到bucket里)
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) { // 原索引+oldCap放到bucket里
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
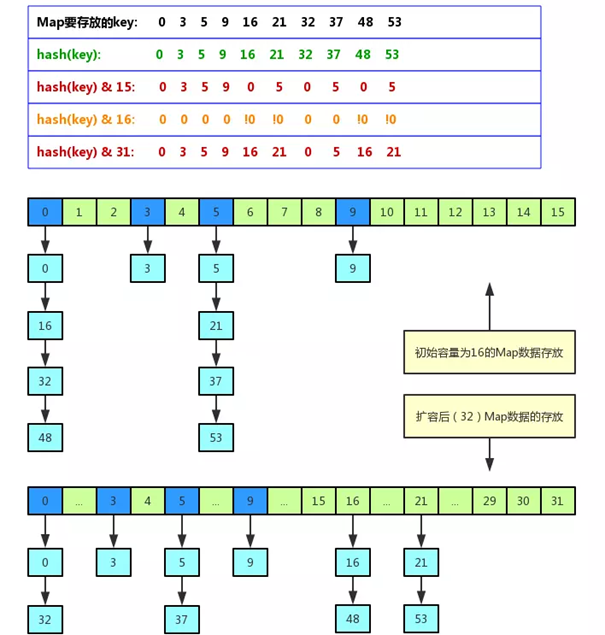
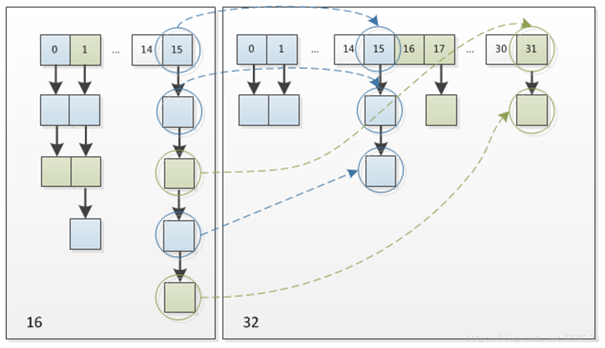
在重新计算链表中元素位置时,只可能得到两个子链表(高链表和低链表):索引不变的元素链表和有相同偏移量的元素链表。在构造子链表的过程中,使用头节点和尾节点,保证了拆分后的有序性:
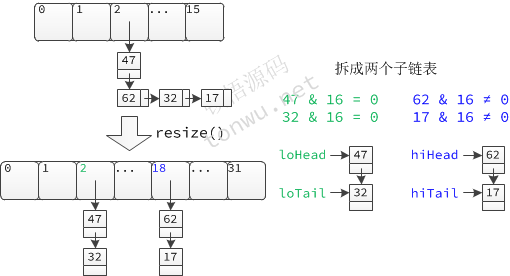
查看 TreeNode.split() 方法发现,红黑树拆分的逻辑和链表一样,只不过在拆分完成后,会根据子链表的长度做以下处理:
- 长度小于 6,返回一个不包含 TreeNode 的普通链表
- 否则,把子链表转为红黑树
红黑树之所以能够按照链表的逻辑拆分,是因为链表在转红黑树时,保留了原链表的链条引用,(node.next )这样也方便了遍历操作。
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;
// Relink into lo and hi lists, preserving order
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD) //长度小于=6
tab[index] = loHead.untreeify(map); //转换成链表
else {
tab[index] = loHead;
if (hiHead != null) // (else is already treeified)
loHead.treeify(tab); //转成红黑树
}
}
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD) //长度小于=6 转换成链表\
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}
其他参考图:
链表转红黑树
链表转红黑树主要做了以下几件事:
- 判断桶容量是否达到树化的最低要求,否则进行扩容
- 将原链表转为由 TreeNode 组成的双向链表
- 将新链表转为红黑树
代码如下:
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize(); // 如果哈希桶容量小于树化的最小容量64,优先进行扩容
else if ((e = tab[index = (n - 1) & hash]) != null) { // 通过hash求出bucket的位置
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null); // 将普通节点转为树形节点TreeNode
if (tl == null)
hd = p;
else {
p.prev = tl; // 把原来的单链表转成了双向链表
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab); // 将TreeNode链表转为红黑树
}
}
TreeNode既是树形结构 又是链表结构 ;
treeify方法:
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
// 以for循环的方式遍历刚才我们创建的链表。
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next; // next向前推进。
x.left = x.right = null;
if (root == null) { // 为树根节点赋值。
x.parent = null;
x.red = false;
root = x;
}
else { // x即为当前访问链表中的项。
K k = x.key;
int h = x.hash;
Class<?> kc = null;
// 此时红黑树已经有了根节点,上面获取了当前加入红黑树的项的key和hash值进入核心循环。
// 这里从root开始,是以一个自顶向下的方式遍历添加。
// for循环没有控制条件,由代码内break跳出循环。
for (TreeNode<K,V> p = root;;) {
// dir:directory,比较添加项与当前树中访问节点的hash值判断加入项的路径,-1为左子树,+1为右子树。
// ph:parent hash。
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p; // xp:x parent。
// 找到符合x添加条件的节点。
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0) // 如果xp的hash值大于x的hash值,将x添加在xp的左边。
xp.left = x;
else // 反之添加在xp的右边。
xp.right = x;
root = balanceInsertion(root, x); // 维护添加后红黑树的红黑结构。
break; // 跳出循环当前链表中的项成功的添加到了红黑树中。
}
}
}
}
moveRootToFront(tab, root);
}
balanceInsertion
第一次循环会将链表中的首节点作为红黑树的根,而后的循环会将链表中的的项通过比较hash值然后连接到相应树节点的左边或者右边,插入可能会破坏树的结构所以接着执行balanceInsertion。
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true; // 正如开头所说,新加入树节点默认都是红色的,不会破坏树的结构。
// 这些变量名不是作者随便定义的都是有意义的。
// xp:x parent,代表x的父节点。
// xpp:x parent parent,代表x的祖父节点
// xppl:x parent parent left,代表x的祖父的左节点。
// xppr:x parent parent right,代表x的祖父的右节点。
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// 如果x的父节点为null说明只有一个节点,该节点为根节点,根节点为黑色,red = false。
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 进入else说明不是根节点。
// 如果父节点是黑色,那么大吉大利,红色的x节点可以直接添加到黑色节点后面,返回根就行了不需要任何多余的操作。
// 如果父节点是红色的,但祖父节点为空的话也可以直接返回根此时父节点就是根节点,因为根必须是黑色的,添加在后面没有任何问题。
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 一旦我们进入到这里就说明了两件是情
// 1.x的父节点xp是红色的,这样就遇到两个红色节点相连的问题,所以必须经过旋转变换。
// 2.x的祖父节点xpp不为空。
// 判断如果父节点是否是祖父节点的左节点
if (xp == (xppl = xpp.left)) {
// 父节点xp是祖父的左节点xppr
// 判断祖父节点的右节点不为空并且是否是红色的
// 此时xpp的左右节点都是红的,所以直接进行上面所说的第三种变换,将两个子节点变成黑色,将xpp变成红色,然后将红色节点x顺利的添加到了xp的后面。
// 这里大家有疑问为什么将x = xpp?
// 这是由于将xpp变成红色以后可能与xpp的父节点发生两个相连红色节点的冲突,这就又构成了第二种旋转变换,所以必须从底向上的进行变换,直到根。
// 所以令x = xpp,然后进行下下一层循环,接着往上走。
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 进入到这个else里面说明。
// 父节点xp是祖父的左节点xppr。
/ 祖父节点xpp的右节点xppr是黑色节点或者为空,默认规定空节点也是黑色的。 // 下面要判断x是xp的左节点还是右节点。
else {
// x是xp的右节点,此时的结构是:xpp左->xp右->x。这明显是第二中变换需要进行两次旋转,这里先进行一次旋转。
// 下面是第一次旋转。
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 针对本身就是xpp左->xp左->x的结构或者由于上面的旋转造成的这种结构进行一次旋转。
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
// 这里的分析方式和前面的相对称只不过全部在右测不再重复分析。
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
下面简述一下前面的两种种幸运的情况
- x本身为根节点返回x。
- x的父节点为黑色或者x的父节点是根节点直接返回不需要变换。
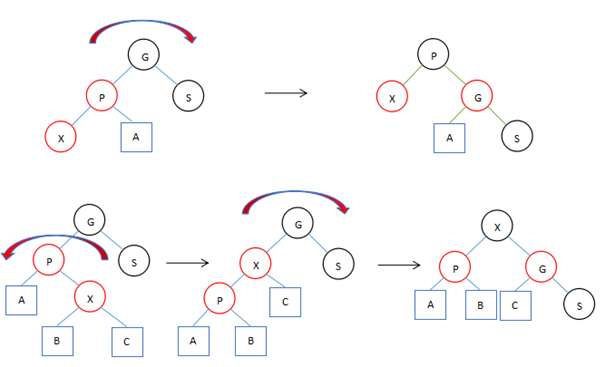
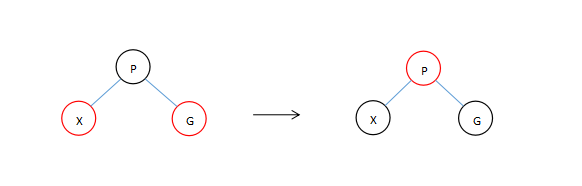
红黑树变色规则
- 单旋转变换。
- 双旋转变换(需要两次反方向的单旋转)。
- 当遇到两个子几点都为红色的话执行颜色变换,因为插入 是红色的会产生冲突。如果根节点两边的子节点都是红色,两个叶子节点变成黑色,根节点变成红色,然后再将根节点变成黑色。
上面的图中描述了红黑树中三种典型的变换,其实前两种变换这正是AVL Tree中的两种典型的变换。
死循环问题
死循环问题在JDK 1.8 之前是存在的,JDK 1.8 通过增加loHead和loTail进行了修复。
在JDK 1.7及之前 HashMap在并发情况下导致循环问题,致使服务器cpu飙升至100%,
下面这个方法就是出现死循环的方法了

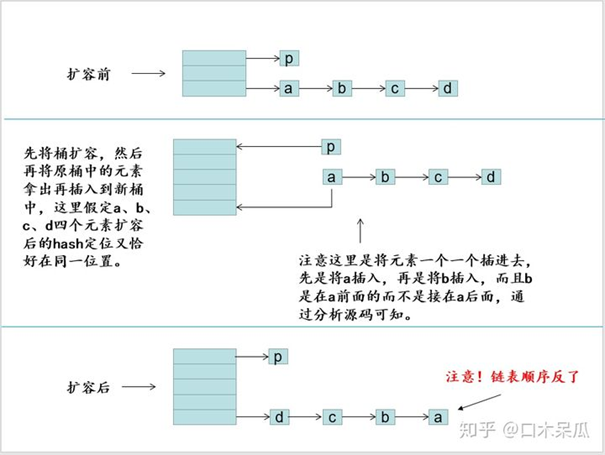
那么当多线程(A、B线程)同时访问我们这段代码时:
现在A线程执行到以下代码时:
Entry<k,v> next = e.next;
线程A交出时间片,线程B这时候接手转移并且完成了元素的转移,这个时候线程A又拿到时间片并接着执行代码:
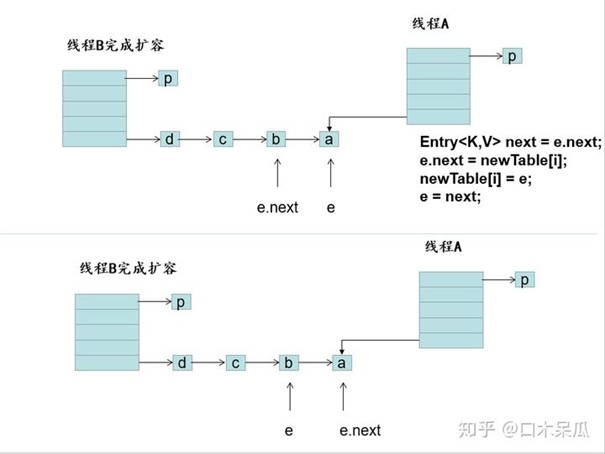
执行后代码如图,当e = a时,这时候这时候再执行:
e.next = newTable[i];// a元素指向了b元素 产生循环
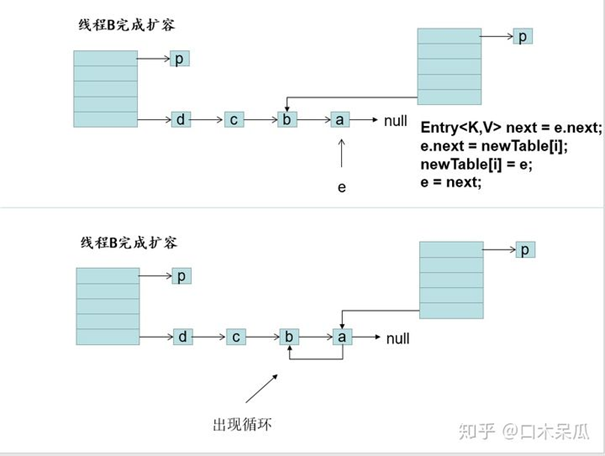
这样链表就就产生了循环,在get元素的时候,线程会一直在环了遍历,无法跳出,从而导致cpu飙升!
参考:
https://my.oschina.net/lienson/blog/3028550
https://www.cnblogs.com/chuonye/p/10907457.html
https://blog.csdn.net/csdn15698845876/article/details/88408804
https://www.cnblogs.com/coloz/p/10598122.html
https://www.cnblogs.com/zhuoqingsen/p/8577646.html
https://blog.csdn.net/lch_2016/article/details/81045480
http://www.importnew.com/31278.html
http://www.importnew.com/22011.html
https://www.cnblogs.com/finite/p/8251587.html
https://www.cnblogs.com/DoubleP/p/11450408.html



