动态规划-最长公共子序列(LCS)

问题

求两个字符串的 LCS ⻓度：

输⼊: str1 = "abcde", str2 = "ace"

输出: 3

解释: 最⻓公共⼦序列是 "ace"，它的⻓度是 3

思路

对于两个字符串的动态规划问题，⼀般来说都是定义 DP table，容易写出状态转移⽅程， dp[i][j] 的状态可以通过之前的状态推导出来：

《算法导论》中关系式如下 :

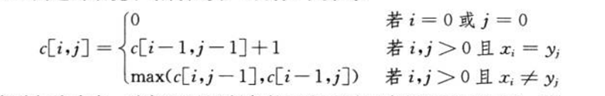
这里的c[i][j] 就是 DP table ;

代码实现

    public static void main(String[] args) {
        String s1 = "abcde";
        String s2 = "ace";
        int len = lcsLength(s1, s2);
        System.out.println("lcs长度:" + len);
    }

 

    public static int lcsLength(String s1, String s2) {
        int m = s1.length();
        int n = s2.length();
        //dp[x][0]和dp[0][x]=0
        int dp[][] = new int[m + 1][n + 1];

        int count = 0;
        //注意,这里 i,j 是从1 开始, 而字符串应该从0开始...
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
                }
                count++;
            }
        }
        System.out.println("循环总次数:" + count);
        return dp[m][n];
    }