Lasso Regression -- subgradient descent algorithm & proximal gradient algorithm
Background

Report
加载数据:
# 加载数据
import numpy as np
import math
import matplotlib as mpl
import matplotlib.pyplot as plt
import torch
plt.rcParams['axes.unicode_minus'] = False # 设置 y 轴正常显示正负号
mpl.rcParams['font.sans-serif'] = ['SimSun'] # 设置宋体字体,以正常显示中文
A = torch.tensor([list(map(float, line.strip().split(' '))) for line in open('A_Lasso.txt')], requires_grad=False)
b = torch.tensor([float(line.strip()) for line in open('b_Lasso.txt')], requires_grad=False)
b = torch.unsqueeze(b, dim=1)
print('A: ', A, 'A.shape:', A.shape)
print('b: ', b, 'b.shape:', b.shape)
xopt = torch.tensor([float(line.strip()) for line in open('xopt.txt')], requires_grad=False)
xopt = torch.unsqueeze(xopt, dim=1)
print('xopt: ', xopt, 'xopt.shape: ', xopt.shape)
全局参数:
n=1000
d=500
step = 0.2 # 步长
Ques (a) - 次梯度下降法

代码:
# 参数
sigma=0.2
var_lambda=2*sigma*math.sqrt(math.log(d)/n)
step1 = step
x0 = torch.zeros((d,1)) # 500 * 1
y = []
# 记录 norm2(x_t - xopt)
norm2_error_1 = [torch.log(torch.norm(x0-xopt, p=2))]
# 目标函数 1/2/n*||Ax - b||^2 + var_lambda*||x||1
def f(x0):
return 1/2/n*torch.matmul((torch.matmul(A,x0)-b).T,torch.matmul(A,x0)-b)+var_lambda*sum(abs(x0))
# 训练
print("start training.")
for i in range(100):
if i % 10 == 0:
if len(y) > 0:
print("step1 " + str(i) + " --- val: " + str(y[len(y) - 1]))
mid_result = f(x0)
y.append(f(x0)) # 存放每次的迭代函数值
# 次梯度, 1/n*A^T(Ax - b) + var_lambda * sign(x)
g0 = 1/n*(torch.matmul(torch.matmul(A.T,A),x0)-torch.matmul(A.T,b) + var_lambda*torch.sign(x0))
step1 = 1/math.sqrt(i+1) # 步长衰减
x1 = x0 - step1*g0
x0 = x1
norm2_error_1.append(torch.log(torch.norm(x0-xopt, p=2)))
y = np.array(y).reshape((100,1))
plt.title('Lasso 回归 -- 次梯度下降法')
plt.ylabel('函数值')
plt.xlabel('迭代次数')
plt.plot(y, 'b', label='f(x)')
plt.legend()
plt.show()
输出图像:
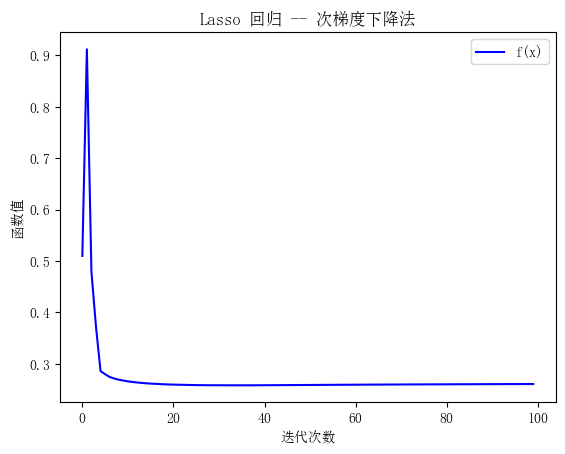
Ques (b) - 邻近点梯度下降法


代码:
p = 0.01 # 正则化参数
epsilon = 1e-5 # 最大允许误差
x_k = torch.zeros((d, 1))
x_k_old = torch.zeros((d, 1))
plot_iteration = [] # 每步计算结果
k = 1 # 迭代次数
# 记录 norm2(x_t - xopt)
norm2_error_2 = [torch.log(torch.norm(x_k_old-xopt, p=2))]
while k < 1e6:
x_k_temp = x_k - step * 1 / n * A.T @ (A@x_k - b) # 对光滑部分做梯度下降
# 临近点投影(软阈值)
for i in range(d):
if x_k_temp[i] < -step * p:
x_k[i] = x_k_temp[i] + step * p
elif x_k_temp[i] > step * p:
x_k[i] = x_k_temp[i] - step * p
else:
x_k[i] = 0
plot_iteration.append(x_k.clone()) # 记录每步计算结果
if torch.norm(x_k - x_k_old) < epsilon:
break
else:
x_k_old = x_k.clone() # 深拷贝
k += 1
norm2_error_2.append(torch.log(torch.norm(x0-x_k, p=2)))
x_optm = x_k[:] # 最优解
plot_dist_optm = [] # 每步结果与最优解的距离
for iter in plot_iteration:
plot_dist_optm.append(torch.norm(iter - x_optm))
plt.title('Lasso 回归 -- 临近点梯度下降法')
plt.xlabel('迭代次数')
plt.ylabel('到最优解的距离')
plt.plot(plot_dist_optm, 'b', label=r'$\| x_k-x_{optm} \|$')
plt.legend()
plt.show()
print(x_optm)
输出图像:
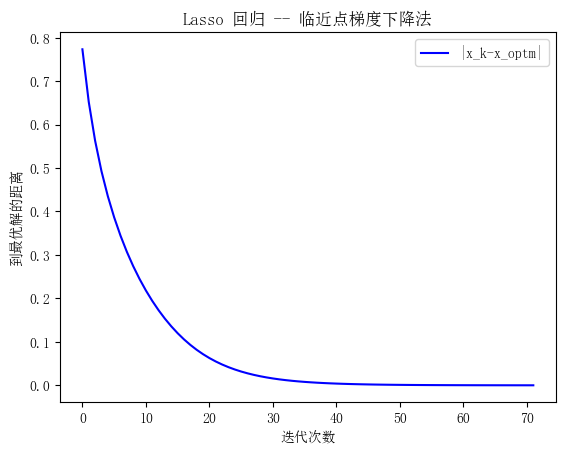
Ques (c) - L2 误差
代码:
plt.title('两种算法的 ' + r'$\ell_2$' + ' 误差')
plt.xlabel('迭代次数')
plt.ylabel(r'$log \| x_t - x^* \|_2$', usetex=True)
plt.plot(norm2_error_1, 'g', label='次梯度下降法')
plt.plot(norm2_error_2, 'b', label='临近点梯度下降法')
plt.legend()
plt.show()
输出图像:
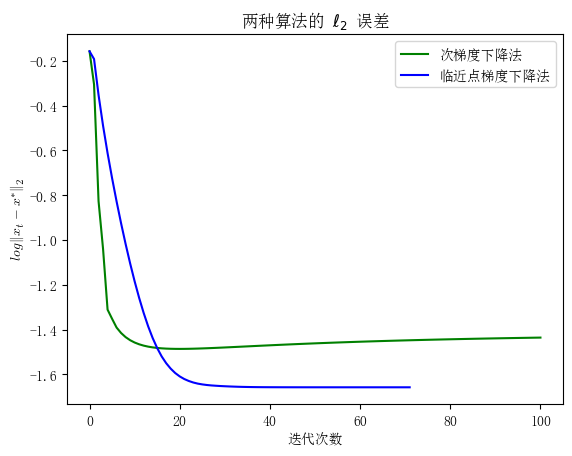
Ques (d) - Comment

由于Lasso函数是convex但不是strongly convex,所以由上表知,邻近点梯度下降算法的收敛速度为\(O(1/t)\),次梯度下降法的收敛速度为\(O(1/\sqrt t)\),即次梯度下降法能够通过更少的迭代次数找到最优解。


