[GAMES101]图形学入门笔记

线性代数基础知识

此处只补充部份线代内容，包括点乘、叉乘和正交。

向量点乘 Vector Dot Product

介绍点乘的基本概念，公式，以及应用。

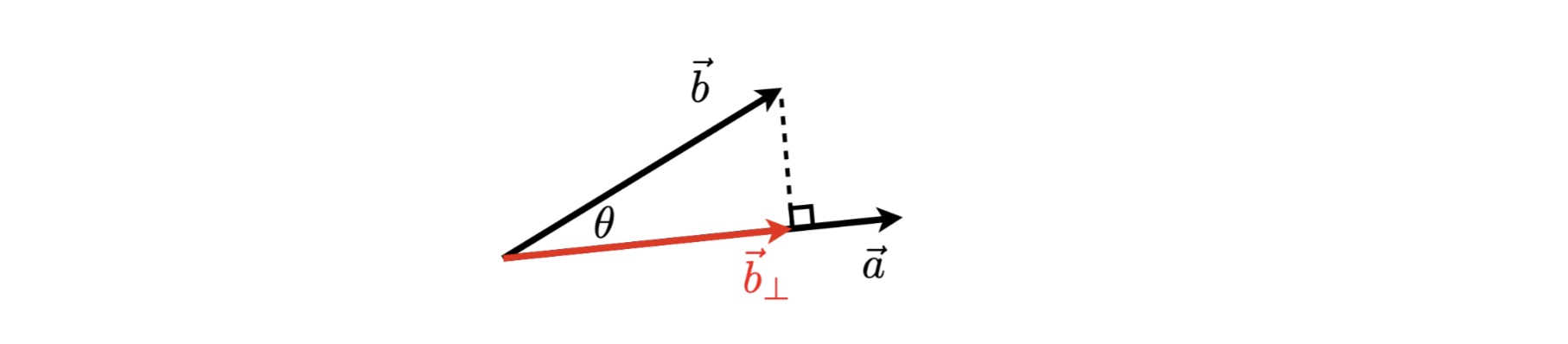
两个向量点乘是一个标量，又是我们也会称其为两个向量的余弦相似度

公式：\(\vec{a} \cdot \vec{b} = ||\vec{a}|| ||\vec{b}|| \cos \theta\)​​

同时也可以获得两个向量的余弦角：\(\cos\theta = \dfrac{\vec{a}\cdot \vec{b}}{||\vec{a}|| ||\vec{b}||}\)​

如果是单位向量的话，模长为1，于是有：\(\cos\theta = \vec{a}\cdot \vec{b}\)

笛卡尔坐标系下的点乘为逐点相乘后相加：

In 2d Cartesian Coordinates:

\[\vec{a} \cdot \vec{b} = \begin{pmatrix} x_a \\ y_a \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b \end{pmatrix} = x_a x_b + y_a y_b \]

In 3d Cartesian Coordinates:

\[\vec{a} \cdot \vec{b} = \begin{pmatrix} x_a \\ y_a \\ z_a \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = x_a x_b + y_a y_b + z_az_b \]

用点乘获得向量投影：

• \(\vec{b}_{\bot}\)表示向量\(\vec{b}\)在向量向量\(\vec{a}\)上的投影
• \(\vec{b}_{\bot}\)方向一定和\(\vec{a}\)的单位向量\(\hat{a}\)同向或反向：\(\vec{b}_{\bot} = k\hat{a}\)
• \(k\)具体值如下：

\[k = ||\vec{b}_{\bot}|| = ||\vec{b}|| \cos \theta \]

点乘在图形学里的一些应用：

1. 测量两个向量的方向差

   用点乘公式获得余弦角。

2. 分解向量：

   利用投影将向量\(\vec{b}\)分解到向量\(\vec{a}\)的方向上，获得\(\vec{b}_\bot\)，然后让\(\vec{b}\)减去该投影向量\(\vec{b}_\bot\)获得剩余向量\(\vec{b} - \vec{b}_\bot\)，获得了\(\vec{b}\)的两组正交向量\(\vec{b}_\bot\)和\(\vec{b} - \vec{b}_\bot\)。

3. 判断两个向量是否是前向/反向：

   点乘的结果是正数，根据公式可知余弦角小于90度，表示两个向量都是前向的；相反如果结果是负数，说明余弦角大于90度，两个向量是反向的。

向量叉乘 Vector Cross Product

两个向量叉乘是一个向量，该向量正交于叉乘的两个向量，方向遵循右手定则，因此叉乘的顺序会改变方向。

叉乘向量的模长公式：\(||\vec{a} \times \vec{b}|| = ||\vec{a}|| ||\vec{b}|| \sin\phi\)

因此显然有：\(\vec{a} \times \vec{b} = -\vec{b} \times \vec{a}\), \(\vec{a} \times \vec{a} = \vec{0}\)

向量叉乘常常用于构建右手坐标系。

笛卡尔坐标系下的叉乘公式：

\[\vec{a} \times \vec{b} = \begin{pmatrix} y_a z_b - y_b z_a \\ z_a x_b - x_a z_b \\ x_a y_b - y_a x_b \end{pmatrix} = A^{*} \vec{b} = \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b\\y_b\\z_b \end{pmatrix} \]

叉乘在图形学里的一些应用：

1. 判断向量\(\vec{b}\)在向量\(\vec{a}\)的左侧还是右侧：

   利用叉乘向量方向遵循右手定则来实现

2. 判断一个点\(P\)是否在三角形\(\triangle ABC\)​的内部：

   按照顺时针或逆时针的顺序，分别叉乘：\(\vec{AP}\times \vec{AB}, \vec{BP}\times \vec{BC}, \vec{CP}\times \vec{CA}\)。如果这几个结果的正负号一致，即点永远在向量的一侧，则该点一定在三角形内部。（可以推广到凸多边形。

正交坐标系 Orthonormal Coordinate Frames

坐标系很重要，有了坐标系就可以表示一些空间中的点和向量了。

往往会存在许多坐标系：Global / Local / Model / parts of model (head, hands, ...)。

需要掌握在不同坐标系下进行相互变换transform。

3D空间中任意三个单位正交向量，满足：

\[\begin{matrix} ||\vec{u}|| + ||\vec{v}|| + ||\vec{w}|| = 1 \\ \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{u} = 0 \\ \vec{w} = \vec{u} \times \vec{v} \quad \text{right-handed} \end{matrix} \]

都可以作为一组正交坐标系。

任意向量\(\vec{p}\)都可以被一组正交坐标系唯一表示：

\[\begin{matrix} \vec{p} = \underbrace{(\vec{p} \cdot \vec{u})}\vec{u} + (\vec{p} \cdot \vec{v}) \vec{v} + (\vec{p} \cdot \vec{w}) \vec{w} \end{matrix} \]

其中\(\vec{p} \cdot \vec{u}\)表示向量\(\vec{p}\)在单位向量\(\vec{u}\)上的投影。

坐标变换

2D坐标变换

我们可以用一个2x2的矩阵对一个2D向量进行变换：

\[\begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} a_{11}x + a_{12}y\\ a_{21}x + a_{22}y \end{pmatrix} \]

上述这种，输入一个2D向量，通过一个简单的矩阵乘法后，输出另一个2D向量的做法称为线性变换。一般来说，我们会考虑沿着x轴或y轴完成一些操作。

Scaling 拉伸

常用的一种变换就是沿着一个坐标系进行拉伸scaling：

\[\operatorname{scale}(s_x,s_y) \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} s_x & 0\\ 0 & s_y \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} s_x x \\ s_y y \end{pmatrix} \]

Shearing 切变

切变变换类似于你把一副卡牌推开的样子，最下面保持不动，越靠近顶部移动的越多。

\[\operatorname{shear-x}(s) = \begin{pmatrix} 1 & s\\ 0 & 1 \end{pmatrix}, \quad \operatorname{shear-y}(s) = \begin{pmatrix} 1 & 0\\ s & 1 \end{pmatrix} \]

Rotation 旋转

定义绕着原点逆时针旋转\(\phi\)的变换如下：

\[\operatorname{rotate}(\phi) \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x\cos\phi - y\sin\phi \\ x\sin\phi + y\cos\phi \end{pmatrix} \]

简单推导：假设原始向量\((x_a,y_a)\)和x轴正方向的夹角为\(\alpha\)，令向量的模长为\(r = \sqrt{x_a^2 + y_a^2}\)，于是有：

\[\begin{cases} x_a = r \cos\alpha \\ y_a = r \sin\alpha \end{cases} \]

则对于逆时针旋转\(\phi\)后的向量\((x_b,y_b)\)，有：

\[\begin{cases} x_b = r \cos(\alpha+\phi) = r\cos\alpha \cos\phi - r\sin\alpha\sin\phi = x_a\cos\phi - y_a\sin\phi\\ y_b = r \sin(\alpha+\phi) = r\sin\alpha\cos\phi + r\cos\alpha\sin\phi =x_a\sin\phi + y_a\cos\phi \end{cases} \]

得证。

Relection 反射

沿着x轴或y轴镜像反射：

\[\operatorname{reflect-y}(s) = \begin{pmatrix} -1 & 0\\ 0 & 1 \end{pmatrix}, \quad \operatorname{reflect-x}(s) = \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \]

齐次坐标系

齐次坐标系是用来解决translation不能写进矩阵变换的问题的，如放射变换：

\[\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix} \]

我们不想让translation操作变成一种特例，想要和前面的linear transform保持一致，于是有了齐次坐标系的概念：

\[\begin{cases} \text{2D point} &= (x, y, \color{red}1 \color{black}) \\ \text{2D vector} &= (x, y, \color{red}0 \color{black}) \\ \end{cases} \]

这里可以简单理解为，点移动是会改变坐标的，但是向量移动后，还是会以原点为起点保持不变。

这也与如下规定保持了一致：

\[\begin{matrix} &向量 &+ &向量 &= &向量 \\ &点 &- &点 &= &向量 \\ &点 &+ &向量 &= &点 \\ &点 &+ &点 &= &点 \end{matrix} \]

在齐次坐标系中，\(\begin{pmatrix} x \\ y \\ w \end{pmatrix} = \begin{pmatrix} x / w \\ y / w \\ 1 \end{pmatrix}\) 表示的是同一个点。\((w\ne 0)\)

于是translation matrix就有了：

\[\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + t_x \\ y + t_y \\ 1 \end{pmatrix} \]

Affine Tansformation 放射变换

Affine transformation = linear map + translation

\[\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix} \]

用了齐次坐标系以后，我们就可以写成：

\[\begin{pmatrix} x' \\ y' \\ w' \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \]

同理有scaling，rotation等，不一一写了。

分解一些复杂的变换

可以简单拆分成三步：

1. 把要旋转的点translate到坐标原点
2. rotate
3. translate回去

3D坐标变换

同样使用齐次坐标系：

\[\begin{cases} \text{3D point} &= (x, y, z, \color{red}1 \color{black}) \\ \text{3D vector} &= (x, y, z, \color{red}0 \color{black}) \\ \end{cases} \]

Affine Transformation:

\[\begin{pmatrix} x' \\ y' \\ z' \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \]