杨氏矩阵学习小记

参考资料：

---

https://blog.csdn.net/acdreamers/article/details/14549077

IOI2019国家预备队论文：袁方舟《浅谈杨氏矩阵在信息学竞赛中的应用》

定义：

---

杨图：

一个n*m的矩阵。

有些格子上有元素，有些没有。

若一个格子没有元素，则它的右边和上边也没有元素。

大概是一个锯齿状的东西：

杨表：

每个位置的元素是一个数字，且是一个排列。

每一行的数从左到右递增，每一列的数从上到下递增：

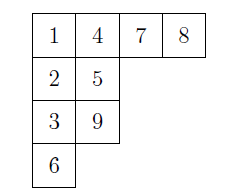
1-n所组成的杨氏矩阵个数：

\[f[1]=1\\ f[2]=2\\ f[n]=f[n-1]+(n-1)f[n-2](n>2) \]

不会证明。

钩子定理

---

知道一个杨图，它的标准杨表个数是：

\((总格子数)!/\prod(每个格子上边格子数+右边格子数+1)\)

不会证明×2。