leetcode116. 填充每个节点的下一个右侧指针

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

 

示例：

输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}

解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

 

提示：

    你只能使用常量级额外空间。
    使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解答：

解法1：递归

对于这个完美二叉树，其实对于每个节点，一共有两步，如图：

 

 

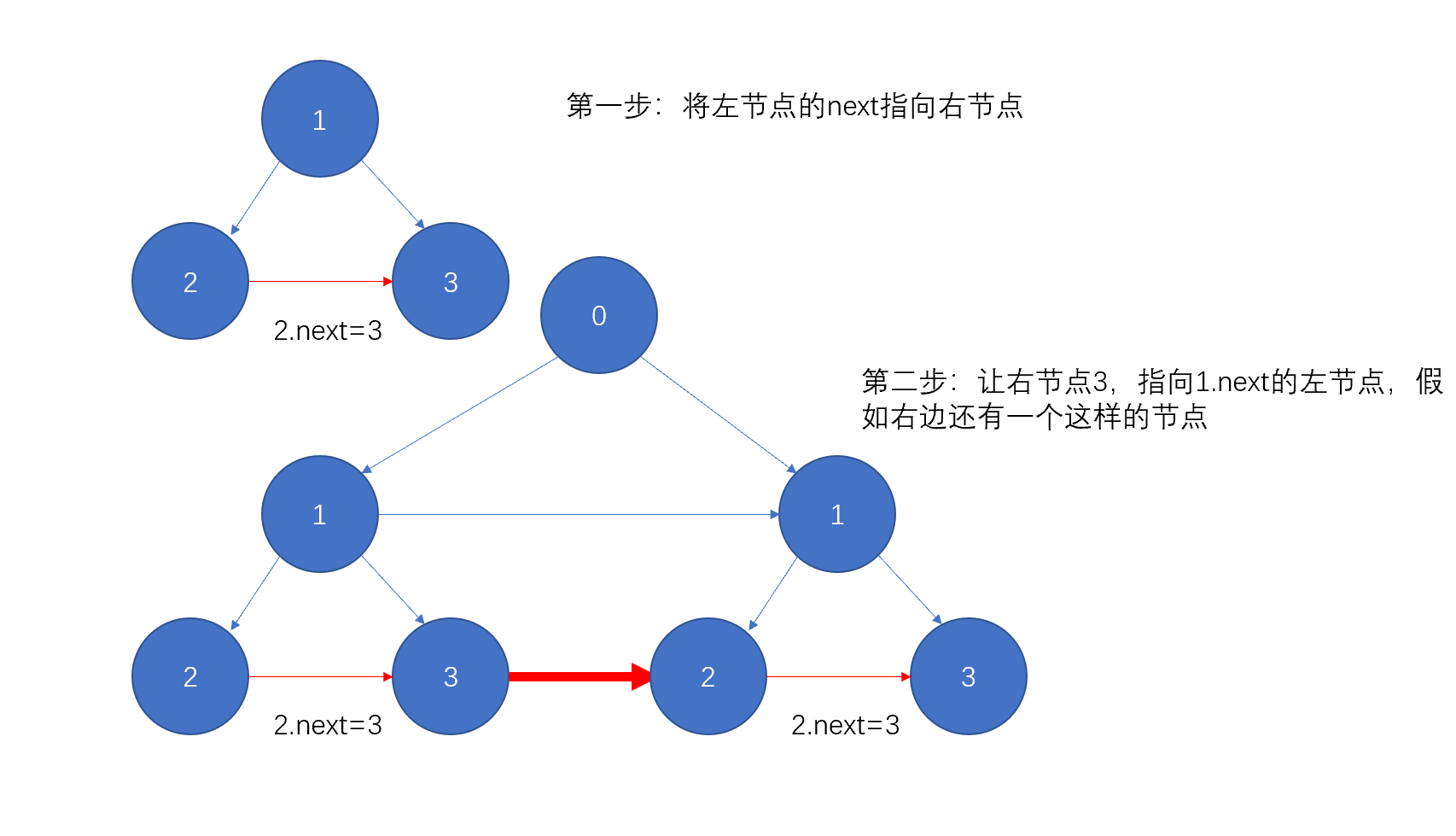
 那么递归的过程就是这么两步，第一步是处理左子树的next，第二步处理右子树的next，那么这个根节点也就完成任务了，就可以往下递归了

也就是往左右子树递归。

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val,Node _left,Node _right,Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/
class Solution {
    public Node connect(Node root) {
        if(root==null||root.left==null)
            return root;
        
        root.left.next=root.right;
        
        if(root.next!=null)
            root.right.next=root.next.left;
        
        connect(root.left);
        connect(root.right);
        return root;
    }
}

 

解法2：迭代

也就是不用list的层序遍历，怎么样才能不用list的额外空间呢？就是用这题目的next指针来引出下一个需要遍历的节点。

这里跟上面的区别就在于一个节点处理完了以后去处理左右子树的递归结构，然而这里不是这样，这里是处理完这一层的结构，再去处理下一层的结构，就这样一层层的遍历到最后一层结束。

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val,Node _left,Node _right,Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/
class Solution {
    public Node connect(Node root) {
        if(root==null)
            return null;
       Node level=root;
        Node worker=root;
        while(level.left!=null)
        {
            worker.left.next=worker.right;
            if(worker.next==null)
            {
                level=level.left;
                worker=level;
            }
            else
            {
                worker.right.next=worker.next.left;
                worker=worker.next;
            }
        }
        return root;
    }
}

解法3：递归的分割法

这里第三种看上去比较爽的，因为是完美二叉树，所以将树的结构分割成两半，将分割成两半的连起来的部分连起来，然后再往左右子树分割，是比较精彩的递归。

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val,Node _left,Node _right,Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/
class Solution {
    public Node connect(Node root) {
        if(root==null)
            return root; 
        Node left=root.left;
        Node right=root.right;
        while(left!=null)
        {
            left.next=right;
            left=left.right;
            right=right.left;
        }
        Node l=connect(root.left);
        Node r=connect(root.right);
        return root;
    }
}