产生在球面上均匀分布的点
如何产生在球面上均匀分布的点呢? 这里提供若干种思路。
1. 生成两个随机分布的角度,并且按照球坐标的形式产生。
缺点: 产生的点是按照角度均匀分布的, 但是注意这并不是球面上均匀分布的点,后面可以看到两极的地方角度明显密集。并且,由于在计算过程中有大量的三角函数的计算,程序的效率不高。
要求不高时可以采用这种方法。
思路是,采用10807 方法产生一组两个随机数,分别作为角度使用。将产生的随机数输出到plt 文件中,使用tecplot绘图。(tecplot是非常好用的CFD后处理可视化的软件,强烈推荐使用)。关于10807 方法产生随机数,有空就另外再开一篇帖子。
下面附上 C++ 代码:

1 #include <iostream> 2 #include<cmath> 3 #include<fstream> 4 5 using namespace std; 6 7 class cRandom 8 { 9 public: 10 cRandom(int x,double y):seed(x),random(y){}; 11 cRandom():seed(0),random(0){}; 12 13 int seed; 14 double random; 15 }; 16 17 cRandom my_random(int z) 18 // 16807 way to create random numbers 19 // z is the seed number, num is the total random number to create 20 { 21 //z(n+1)=(a*z(n)+b) mod m 22 //describe m=a*q+r to avoid that the number is large than the computer can bear 23 const int m=pow(2,31)-1; 24 const int a=16807; 25 const int q=127773; 26 const int r=2836; 27 28 int temp=a*(z%q)-r*(z/q); 29 30 if(temp<0) 31 { 32 temp=m+temp; 33 } 34 //z is the seed number 35 z=temp; 36 double t = z*1.0/m; 37 38 cRandom cr; 39 cr.random=t; 40 cr.seed=z; 41 42 return cr; 43 } 44 45 int main() 46 { 47 cout << "Hello world!" << endl; 48 const int num = pow(10,5); 49 int z1 = 20; 50 int z2=112; 51 52 ofstream fcout; 53 fcout.open("result.plt"); 54 fcout<<" title=random "<<endl; 55 fcout<<" VARIABLES = \"X\",\"Y \",\"Z \" "<<endl; 56 fcout<<"zone I= "<<num<<",datapacking=POINT"<<endl; 57 cRandom sita(z1,0.0); 58 cRandom pesi(z2,0.0); 59 const double pi = 3.141592; 60 61 for(int i=0;i!=num;++i) 62 { 63 sita=my_random(pesi.seed); 64 pesi=my_random(sita.seed); 65 66 double x=1.0*sin(pi*sita.random)*cos(2*pi*pesi.random); 67 double y=1.0*sin(pi*sita.random)*sin(2*pi*pesi.random); 68 double z=1.0*cos(pi*sita.random); 69 70 fcout<<x<<" "<<y<<" " <<z<<endl; 71 } 72 73 74 fcout.close(); 75 fcout<<"this program is finished"<<endl; 76 77 return 0; 78 }
效果图是这样滴:
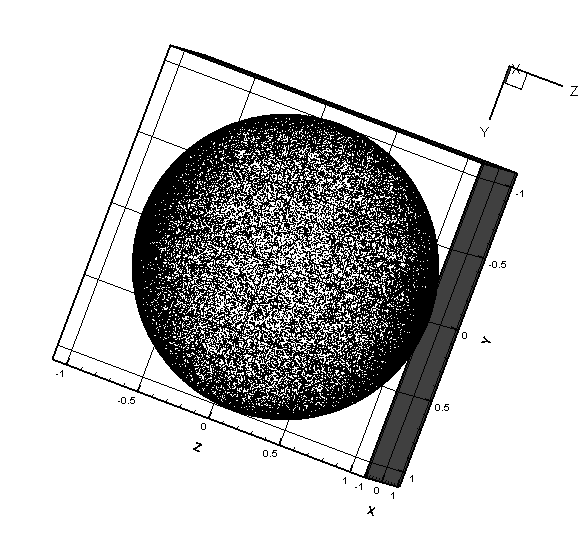
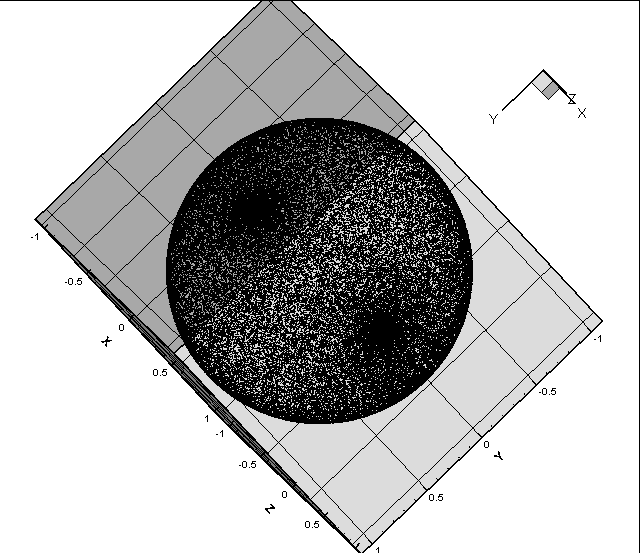
可以看到在两级的地方点明显的密集。
不要担心,我们还有更漂亮更快速的方式产生球面上的均匀的点。
2. 三维球面上的Marsaglia 方法
这是一种基于变换抽样的方法,产生的结果非常漂亮。原理我会单开一篇帖子讲述,这里仅仅给出实行的方法。
step1:
随机抽样产生一对均匀分布的随机数 u ,v ;这里u,v 在[-1,1] 范围内
step2 :
计算 r^2 = u^2+v^2;
如果 r^2 > 1 则重新抽样,直到满足 r^2 < 1 .
step3 :
计算
x=2*u*sqrt(1-r2);
y=2*v*sqrt(1-r2);
z=1-2*r2;
好了,基本原理非常简单,直接上代码:

1 #include <iostream> 2 #include<cmath> 3 #include<fstream> 4 5 using namespace std; 6 7 class cRandom 8 { 9 public: 10 cRandom(int x,double y):seed(x),random(y){}; 11 cRandom():seed(0),random(0){}; 12 13 int seed; 14 double random; 15 }; 16 17 cRandom my_random(int z) 18 // 16807 way to create random numbers 19 // z is the seed number, num is the total random number to create 20 { 21 //z(n+1)=(a*z(n)+b) mod m 22 //describe m=a*q+r to avoid that the number is large than the computer can bear 23 const int m=pow(2,31)-1; 24 const int a=16807; 25 const int q=127773; 26 const int r=2836; 27 28 int temp=a*(z%q)-r*(z/q); 29 30 if(temp<0) 31 { 32 temp=m+temp; 33 } 34 //z is the seed number 35 z=temp; 36 double t = z*1.0/m; 37 38 cRandom cr; 39 cr.random=t; 40 cr.seed=z; 41 42 return cr; 43 } 44 45 int main() 46 { 47 cout << "Hello world!" << endl; 48 const int num = pow(10,5); 49 int z1 = 20; 50 int z2=112; 51 52 ofstream fcout; 53 fcout.open("result.plt"); 54 fcout<<" title=random "<<endl; 55 fcout<<" VARIABLES = \"X\",\"Y \",\"Z \" "<<endl; 56 fcout<<"zone I= "<<num/2<<",datapacking=POINT"<<endl; 57 cRandom sita(z1,0.0); 58 cRandom pesi(z2,0.0); 59 60 61 for(int i=0;i!=num;++i) 62 { 63 sita=my_random(pesi.seed); 64 pesi=my_random(sita.seed); 65 66 double u=2*sita.random-1.0; 67 double v=2*pesi.random-1.0; 68 69 double r2=pow(u,2)+pow(v,2); 70 if(r2<1) 71 { 72 double x=2*u*sqrt(1-r2); 73 double y=2*v*sqrt(1-r2); 74 double z=1-2*r2; 75 76 fcout<<x<<" "<<y<<" " <<z<<endl; 77 } 78 } 79 80 fcout.close(); 81 fcout<<"this program is finished"<<endl; 82 83 return 0; 84 }
效果图是这样的(360°无死角均匀):
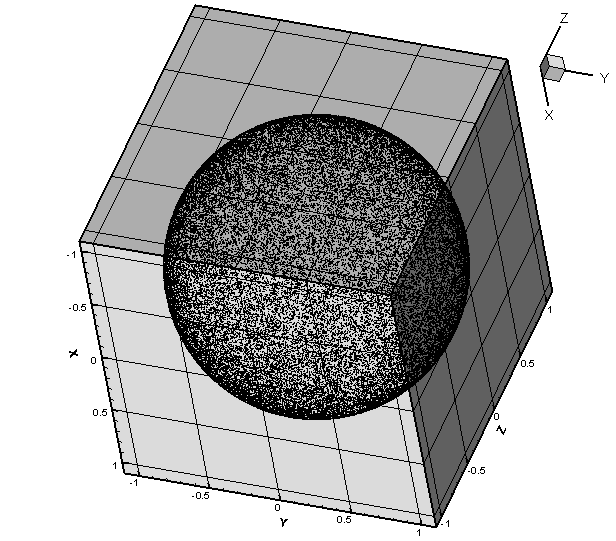

3. 直接抽样法产生球面上均匀分布的点
这种方法是使用直接抽样法,产生球面上随机分布的点,与变换抽样法不同。
1 #include <iostream> 2 #include <fstream> 3 #include<cmath> 4 using namespace std; 5 6 double is_independence(const int N); 7 8 void my_random(ofstream & fcout,const int num,int z) 9 // 16807 way to create random numbers 10 // z is the seed number, num is the total random number to create 11 { 12 //z(n+1)=(a*z(n)+b) mod m 13 //describe m=a*q+r to avoid that the number is large than the computer can bear 14 const int m=pow(2,31)-1; 15 const int a=16807; 16 const int q=127773; 17 const int r=2836; 18 19 for (int i=0;i!=num;++i) 20 { 21 int temp=a*(z%q)-r*(z/q); 22 23 if(temp<0) 24 { 25 temp=m+temp; 26 } 27 //z is the seed number 28 z=temp; 29 double t = z*1.0/m; 30 31 fcout<<t<<endl; 32 } 33 } 34 35 void my_randomz(ofstream & fcout,const int num,int z) 36 // another way to create random numbers 37 { 38 const int m=100000001; 39 const int a=329; 40 const int q=303951; 41 const int r=122; 42 43 for (int i=0;i!=num;++i) 44 { 45 int temp=a*(z%q)-r*(z/q); 46 47 if(temp<0) 48 { 49 temp=m+temp; 50 } 51 z=temp; 52 double t = z*1.0/m; 53 54 fcout<<t<<endl; 55 } 56 } 57 58 double is_uniform(const int N,const int K) 59 //judge whether the random is uniform 60 { 61 62 ifstream fcin; 63 fcin.open("re2.dat"); 64 double esp(0); 65 double total(0); 66 for (int i = 0; i != N; ++ i) 67 { 68 double temp; 69 fcin>>temp; 70 total += pow(temp,K); 71 } 72 esp = total/N-1.0-1/(K+1); 73 fcin.close(); 74 return esp; 75 } 76 77 double is_independence(const int N) 78 //judge whether the randoms are independence 79 { 80 ifstream fcin; 81 fcin.open("re2.dat"); // open the file 82 if(!fcin) 83 { 84 cout<<"error! :open file error!"<<endl; 85 return -1.0; 86 } 87 88 double esp(0); 89 double xSq(0); 90 double x(0); 91 double xy(0); 92 93 double temp(0); //start to input the random number 94 fcin>>temp; 95 double oldTemp(0); 96 97 for(int i=0;i!=N;++i) 98 { 99 oldTemp=temp; 100 101 x+=temp; 102 xSq+=temp*temp; 103 104 fcin>>temp; 105 xy +=temp*oldTemp; 106 } 107 108 fcin.close(); 109 110 double cResult(0); 111 cResult=(xy-x*x)/(xSq-x*x); 112 return cResult; 113 } 114 115 int main() 116 { 117 cout<<"hello,world!"<<endl; 118 int num=pow(10,7); //the total number of randoms 119 int z=45; //the seed of the program 120 /* 121 // get random number using 10807 and another way 122 //save the result in two files 123 124 ofstream fcout; 125 fcout.open("re1.dat"); 126 my_random(fcout,num,z); //call 16807 way to create random number 127 fcout.close(); 128 fcout.open("re2.dat"); 129 my_randomz(fcout,num,z); //call 16807 way to create random number 130 fcout.close(); 131 */ 132 133 //const int N = pow(10,3); // the number of the random 134 int N(0); 135 cout<<"inter the number of the checked number:"<<endl; 136 cin >> N; 137 138 const int K = 10; //the section number divide 139 double esp(0); 140 esp=is_uniform(N,K); 141 cout<<"uniform number is "<<"esp="<<esp<<endl; 142 143 esp=is_independence(N); 144 cout<<"indenpendence number is "<<"esp="<<esp<<endl; 145 146 return 0; 147 }
4.力学方法产生。
这种方法是基于力学原理产生的,球面上的点是主动运动的,他们相互排斥,直到一个最均匀的状态。
这里是传送门: http://zhidao.baidu.com/link?url=hN6nj60BC0RvMZorGtT6VToPH2T9cXcC26MwL2G94e_nFSUPXUstInmXxwydCx-0PI3l4jlKnCv2ZvyLrVsA4oe3b-3PldLS2V2D-hcH0OO
思路是: 对球面上的每一个点施加 坐标: x,y,z; 施加速度,vx,vy,vz ; 计算其余点对当前点的作用力,求解一个微分方程组。初始状态随机分布,每一个计算步更新当前粒子的运动速度和位移。
传送门的matlab代码:

function []=main() N=12; %点数量 a=rand(N,1)*2*pi; %根据随机求面均匀分布,先生成一个初始状态 b=asin(rand(N,1)*2-1); r0=[cos(a).*cos(b),sin(a).*cos(b),sin(b)]; v0=zeros(size(r0)); G=1e-2;%斥力常数,试验这个值比较不错 for ii=1:200%模拟200步,一般已经收敛,其实可以在之下退出 [rn,vn]=countnext(r0,v0,G);%更新状态 r0=rn;v0=vn; end plot3(rn(:,1),rn(:,2),rn(:,3),'.');hold on;%画结果 [xx,yy,zz]=sphere(50); h2=surf(xx,yy,zz); %画一个单位球做参考 set(h2,'edgecolor','none','facecolor','r','facealpha',0.7); axis equal; axis([-1 1 -1 1 -1 1]); hold off; end function [rn vn]=countnext(r,v,G) %更新状态的函数 %r存放每点的x,y,z数据,v存放每点的速度数据 num=size(r,1); dd=zeros(3,num,num); %各点间的矢量差 for m=1:num-1 for n=m+1:num dd(:,m,n)=(r(m,:)-r(n,:))'; dd(:,n,m)=-dd(:,m,n); end end L=sqrt(sum(dd.^2,1));%各点间的距离 L(L<1e-2)=1e-2; %距离过小限定 F=sum(dd./repmat(L.^3,[3 1 1]),3)';%计算合力 Fr=r.*repmat(dot(F,r,2),[1 3]); %计算合力径向分量 Fv=F-Fr; %切向分量 rn=r+v; %更新坐标 rn=rn./repmat(sqrt(sum(rn.^2,2)),[1 3]); vn=v+G*Fv;%跟新速度 end





