求数组中的逆序对的数量----剑指offer36题

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数：

如数组{7,5,6,4}，逆序对总共有5对，{7,5}，{7,6}，{7,4}，{5,4}，{6,4}；

思路1：暴力解法，顺序扫描整个数组，每扫描到一个数字的时候，逐个比较该数字和它后面的数字的大小。如果后面的数字比它小，则这两个数字就组成一个逆序对。假设数组中含有n个数字，由于每个数字都要和O(n)个数字作比较，因此这个算法的时间复杂度是O(n2)。

思路2：分治思想，采用归并排序的思路来处理，如下图，先分后治：

 

先把数组分解成两个长度为2的子数组，再把这两个子数组分解成两个长度为1的子数组。接下来一边合并相邻的子数组，一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7>5，因此（7,5）组成一个逆序对。同样在第二对长度为1的子数组{6}，{4}中也有逆序对（6,4），由于已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组进行排序，避免在之后的统计过程中重复统计。

逆序对的总数=左边数组中的逆序对的数量+右边数组中逆序对的数量+左右结合成新的顺序数组时中出现的逆序对的数量；

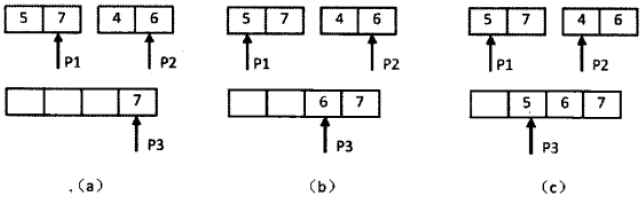
总结统计数组逆序对的过程：先把数组分隔成子数组，先统计出子数组内部的逆序对的数目，然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中，还需要对数组进行排序，其实这个排序过程就是归并排序的思路。

代码实现思路如下：

//数组中的逆序对
    public static int InversePairs(int[] array){
        if(array==null||array.length<=1)
            return 0;
        int[] copy = new int[array.length];
        for(int i=0;i<array.length;i++){
            copy[i] = array[i];
        }
        return mergeCount(array, copy, 0, array.length-1);
    }
    
    public static int mergeCount(int[] array, int[] copy, int start, int end){
        if(start==end){
            copy[start] = array[start];
            return 0;
        }
        int mid = (start+end)>>1;
        int leftCount = mergeCount(copy, array, start, mid);
        int rightCount = mergeCount(copy, array, mid+1, end);
        
        int i = mid;//i初始化为前半段最后一个数字的下标
        int j = end;//j初始化为后半段最后一个数字的下标
        int index = end;//辅助数组复制的数组的最后一个数字的下标
        int count = 0;//计数--逆序对的数目
        while(i>=start&&j>=mid+1){
            if(array[i]>array[j]){
                copy[index--] = array[i--];
                count += j-mid;
            }else{
                copy[index--] = array[j--];
            }
        }
        for(;i>=start;i--){
            copy[index--] = array[i];
        }
        for(;j>=mid+1;j--){
            copy[index--] = array[j];
        }
        return leftCount+rightCount+count;
    }