胡不归问题

简介

本文有大篇幅转载。如侵犯您的版权，请联系qq3239315078.

胡不归出处： 先秦《国风·邶风·式微》 式微，式微，胡不归？微君之故，胡为乎中露！

胡不归问题，是一个非常古老的数学问题，曾经是历史上非常著名的“难题”。近年来陆续成为各地中考模拟题的小热门考点，学生不易把握，今天给大家普及讲解一下。

有一个很美的故事，不知大家是否听说过。

话说，从前有一小伙子外出务工，某天不幸得知老父亲病危的消息，便立即赶路回家．小伙子略懂数学常识，考虑到“两点之间线段最短”的知识，就走布满沙石的路直线路径，而忽视了走折线虽然路程多但速度快的实际情况，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”

这个问题引起了人们的思索，小伙子能否节省路上时间提前到家？如果可以，他应该选择一条怎样的路线呢？这就是流传千百年的“胡不归问题．

讲解

 

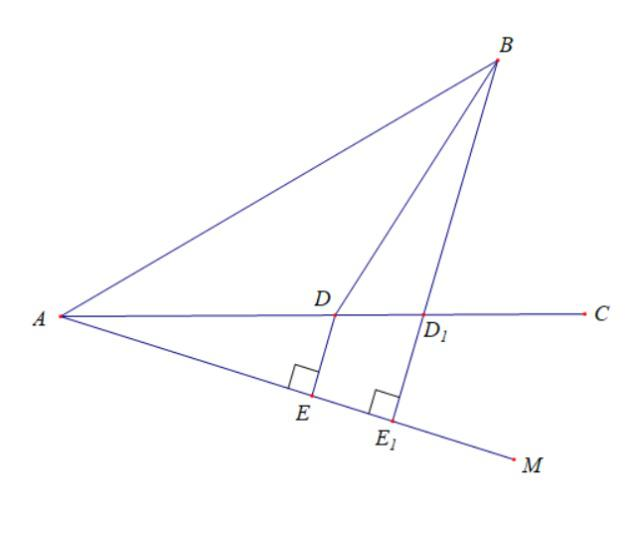
上述数学解释用到了三角函数知识将两个线段的系数权重都化为1，从而降低了求最值难度。聪明的同学或许一下就发现转化成了我之前讲过的“将军饮马（小河取水）”模型，进而作对称求得最值。

 

例题

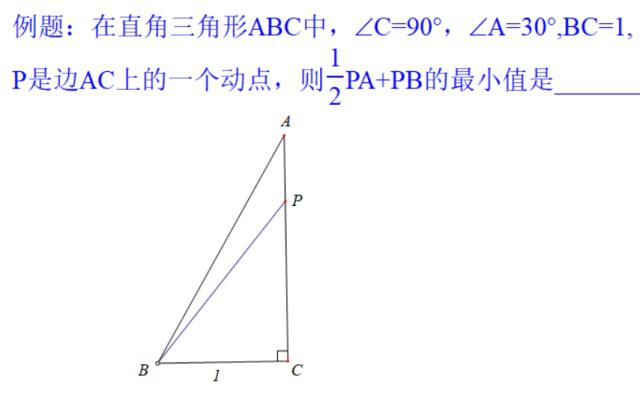
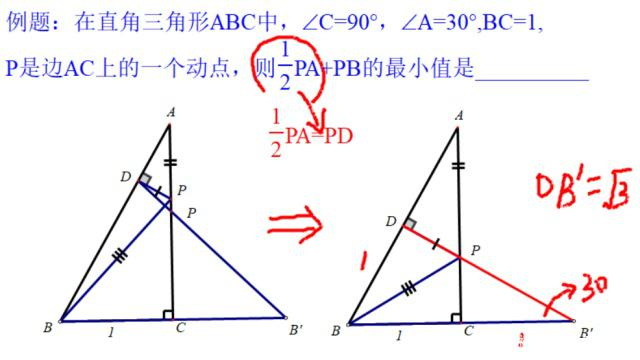
显然线段PA,PB的系数不同，先要将他们化为1.考虑到本题中有个∠A=30°，而30°所对的直角边是斜边的一半，所以可以将二分之一PA转化，如图

 

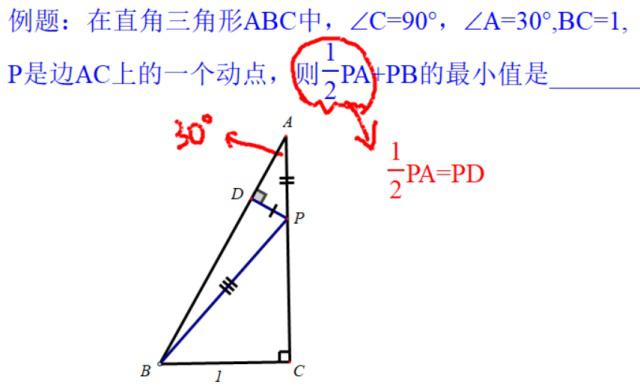
然后问题就明朗了，系数都是1了，得到新模型——“将军饮马（小河取水）”模型

 

 

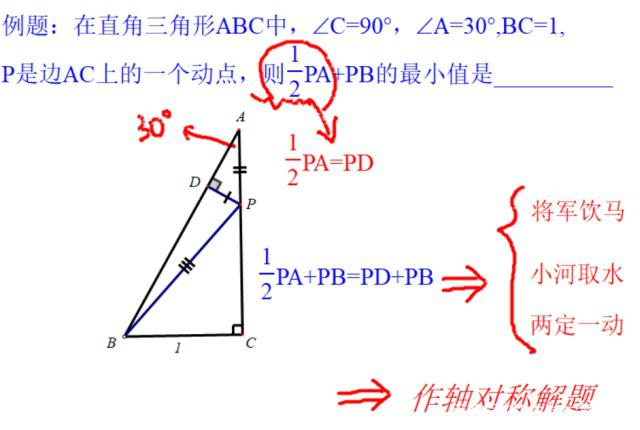
剩下的问题就是作对称，求最值了。大家思考一下，该选取哪个点关于AC对称比较好？是D点呢，还是B点呢？

聪明的你肯定注意到了∠C=90°，所以我们选取B点关于AC对称比较好，方便计算。如下图：

 

 

 

 

结语

DB’和AB垂直时候，DB’就是本题的最短线段（所用知识：两点之间线段最短+垂线段最短）。容易知道B’也是30°，可知BD=BC=1,而DB’是DB的根号3倍，为根号3.

 

本题综合性强，是对动点最值问题的全面考察，鼓起勇气向难题亮剑！

话说，从前有一小伙子外出务工，某天不幸得知老父亲病危的消息，便立即赶路回家．小伙子略懂数学常识，考虑到“两点之间线段最短”的知识，就走布满沙石的路直线路径，而忽视了走折线虽然路程多但速度快的实际情况，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”