Melkman算法处理凸包问题

文章首发于我的个人网站：https://www.codinglink.tech/articles/the-melkman-algorithm-deals-with-the-problem-of-convex-packets.html

Melkman算法是1985年Avraham A. Melkman在其在线简单折线的凸包的在线构造中引入的。他提出了复杂度为O(n)的增量算法计算。简单之处是使用了双向表的方法来实现。

算法思想：

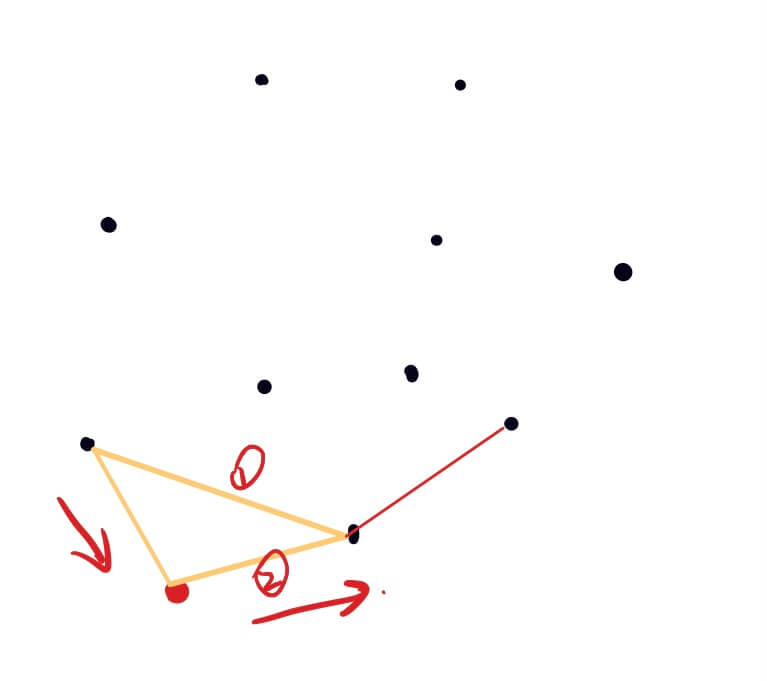
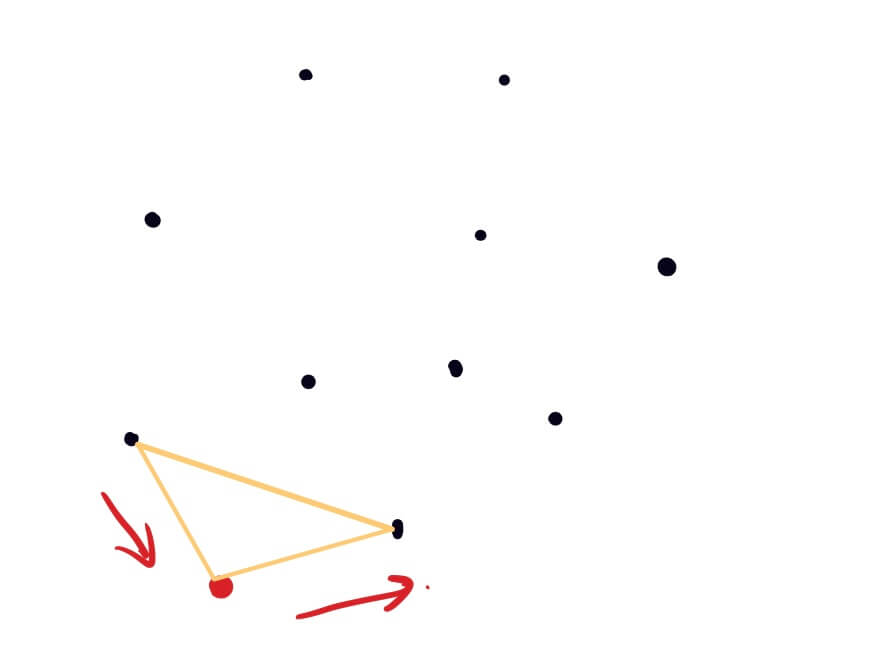
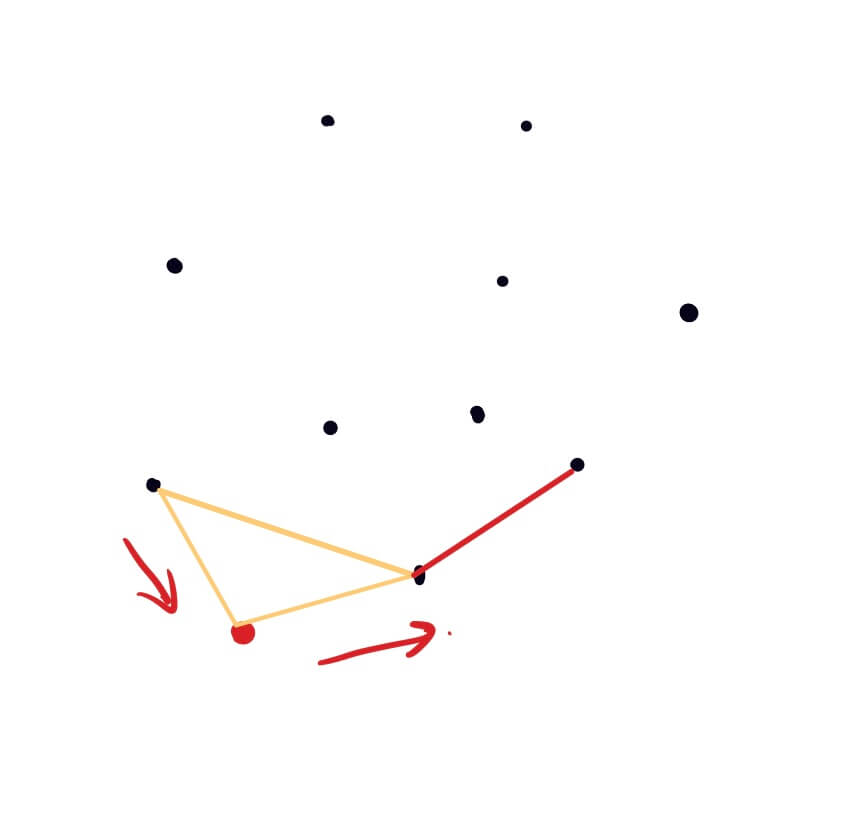
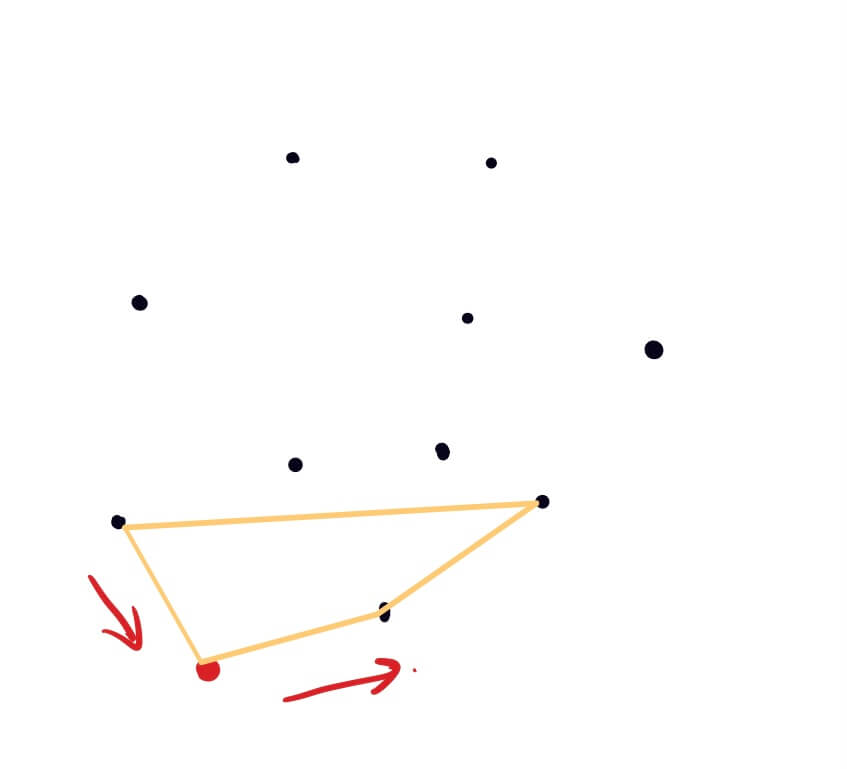
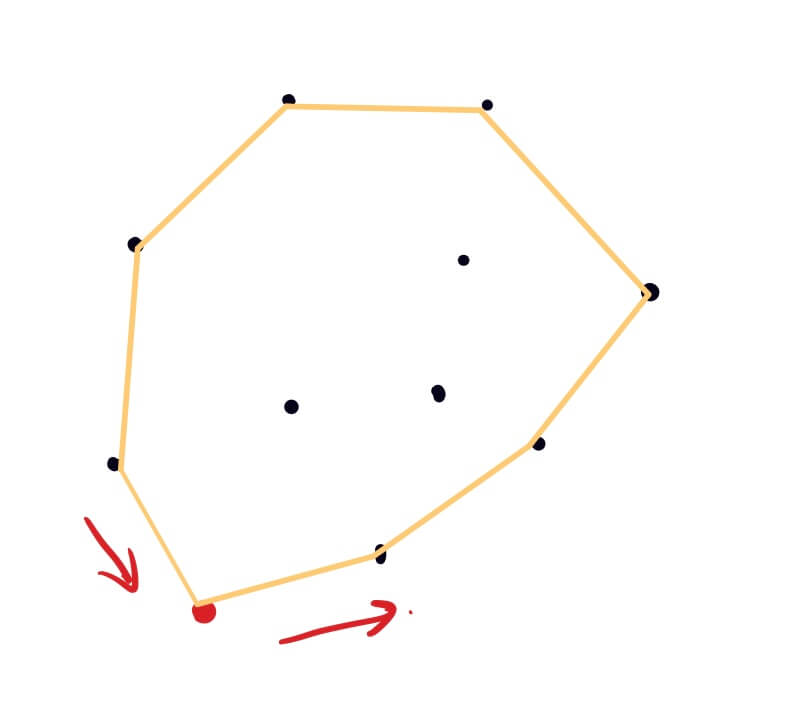
逐个比较所给点的y坐标值，选出y坐标最大的点，若两个点的y坐标值相同时，取x坐标最小的点，并将该点作为该点集的第一个元素；
计算出其他所有点与y坐标最小点的斜率，并将点集按照斜率从小到大排序；
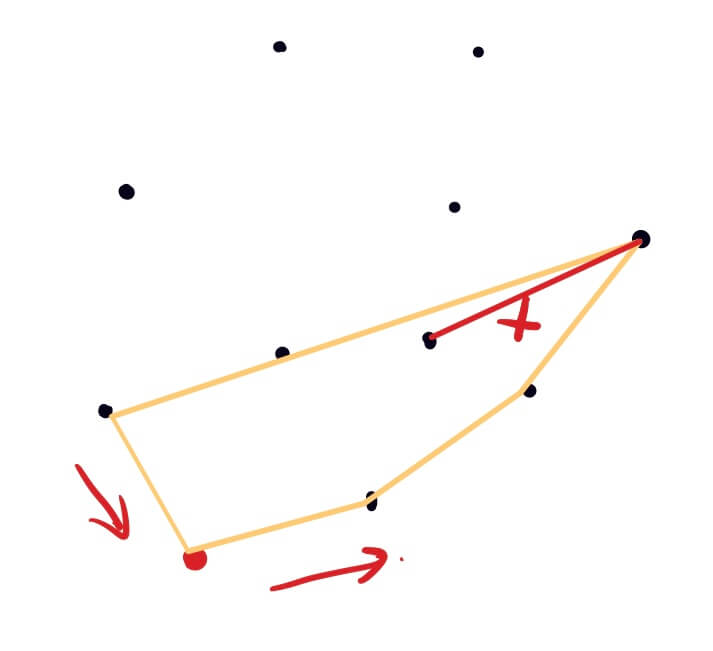
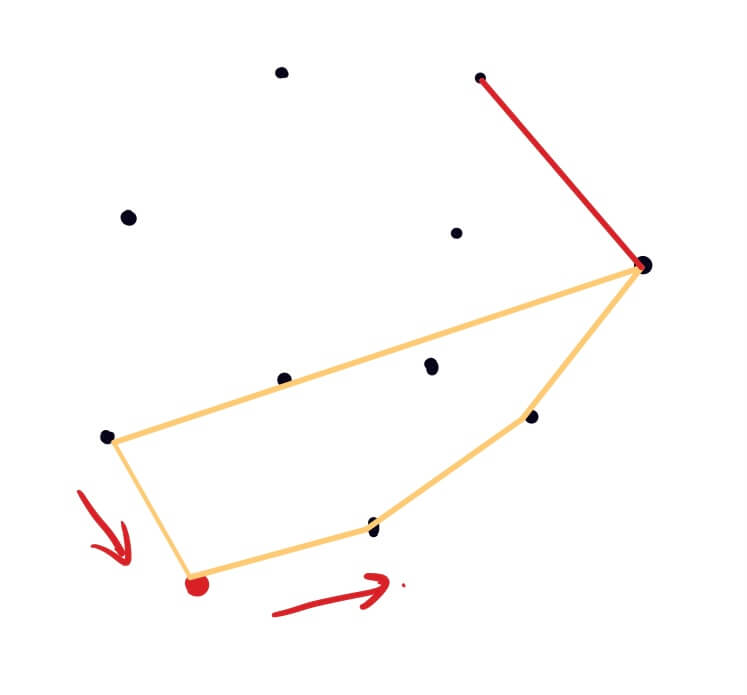
第一次首先找出第一个点的左右相邻的两个点，构成三角形，如果初始的点与该点相邻的两个点共线，则依次找下一个点；
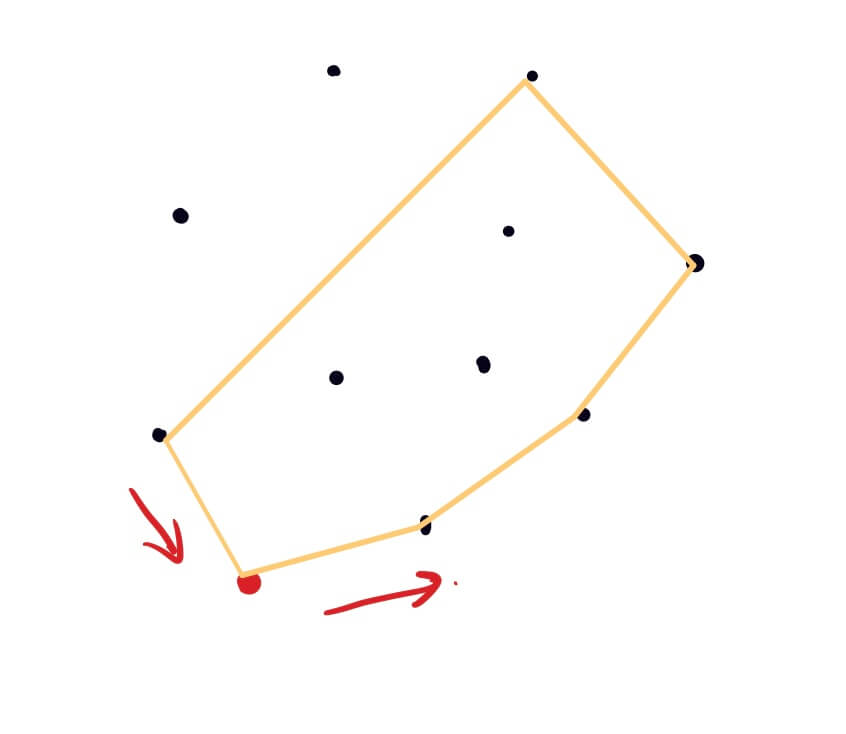
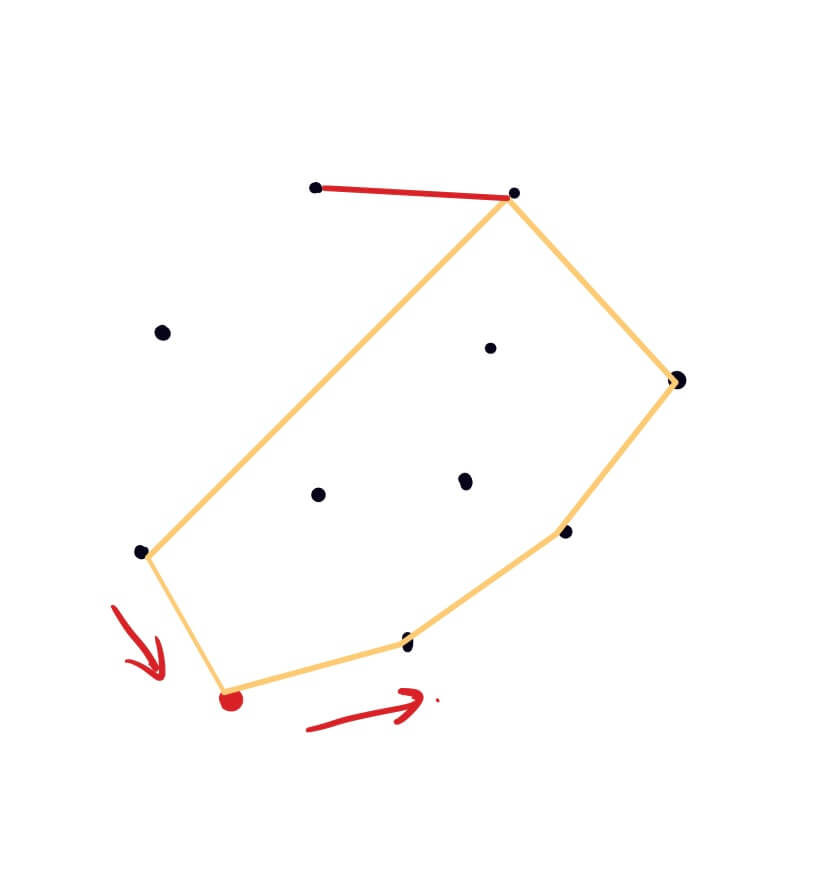
整个查找按照逆时针方向，判断当前点是不是在凸包内部，则去掉上一个点（因为该点在凸包内），将当前点添加到凸包上的点集中；
直到查找到最后一个点结束，此时该点集的左右两端为同一点，即形成闭包。

注：首先将初始点（y坐标最小的点）放在所求点集的中间，分别向该点的左右两边添加元素。因为该双向表的两端的元素相同，所以满足上一点的两条边和当前点与上一点连成的直线均向左转则判定点在直线内。

C++代码：

#include<iostream>
#include<sstream>
#include<cstring>
#include<fstream>
using namespace std;
#define MaxSize 500

/**
* 建立点的坐标的结构体
*/
typedef struct
{
    double x;
    double y;
    double angle;
}Point;

Point points[MaxSize];//用于存储原始数据
Point results[MaxSize];//用于存储结果
int PointsNum = 0, xRange = 0, yRange = 0;//分别为点的个数，x的范围，y的范围
int index[MaxSize];//数组索引，双向表




/**
* 读取文件的方法
*/
int readData(string fn)
{
    //string s;
    int flag = 0;//作为判断是否为第一次读取的标志
    //static int x[MaxSize] = { 0 }, y[MaxSize] = { 0 };
    int i = 0;//计数
    char t = NULL;//存储非数字的符号
    ifstream fin(fn, ios::in);
    if (fin.fail())
    {
        cout << "无法打开该文件";
        return 0;
    }
    while (!fin.eof())
    {
        if (flag == 0)
        {
            //在第一次读取时分别读取点数，x的最大值，y的最大值，按行读取
            fin >> PointsNum >> t >> xRange >> t >> yRange;
            flag = 1;
        }

        /**
        * 分别读取点的坐标，t作为临时变量存储括号和逗号
        */
        int a, b;
        fin >> t >> a >> t >> b >> t;
        points[i].x = a;
        points[i].y = b;
        i++;
    }
    return i - 1;

}

/**
* 信息写入txt文件的方法
*/
void wtriteData(string output)
{

}
/**
 * 点集的元素位置交换
 *
 */
void swap(int i, int j)
{
    Point tempPoint;
    tempPoint.x = points[j].x;
    tempPoint.y = points[j].y;
    tempPoint.angle = points[j].angle;

    points[j].x = points[i].x;
    points[j].y = points[i].y;
    points[j].angle = points[i].angle;

    points[i].x = tempPoint.x;
    points[i].y = tempPoint.y;
    points[i].angle = tempPoint.angle;
}

/**
 * 移动起点
 * 返回移动后的位置
 */
int loc(int top, int bot)
{
    double x = points[top].angle;
    int j, k;
    j = top + 1;
    k = bot;
    while (true)
    {
        while (j < bot && points[j].angle < x)
            j++;
        while (k > top && points[k].angle > x)
            k--;
        if (j >= k)
            break;
        swap(j, k);
    }
    swap(top, k);
    return k;
}

/**
 * 快速排序
 */
void quickSort(int top, int bot)
{
    int pos;
    if (top < bot)
    {
        pos = loc(top, bot);
        quickSort(top, pos - 1);
        quickSort(pos + 1, bot);

    }
}

/**
* 判断是否为左转
* 通过行列式D=(x1-x2)*(y3-y2)-(x3-x2)*(y1-y2)得到
* 当行列式值为正时，则反时针（左）转，当行列式值为负时，则顺时针（右）转。行列式值为0当且仅当三点共线。
*/
double isLeft(Point o, Point a, Point b)
{
    double aoX = a.x - o.x;
    double aoY = a.y - o.y;
    double baX = b.x - a.x;
    double baY = b.y - a.y;
    return aoX * baY - aoY * baX;
}

void getResults(Point points[], int PointsNum)
{
    int k = 0;
    Point Ymin;
    Ymin.x = 32767;
    Ymin.y = 32767;
    for (int i = 0; i < PointsNum; i++)
    {
        /**
        * 找出y值最小的点
        * 返回点的序号
        */
        if (points[i].y < Ymin.y)
        {
            Ymin.x = points[i].x;
            Ymin.y = points[i].y;
            k = i;
        }
        /**
        * 如果两个点的x坐标相等
        * 则判断两个点的y坐标，谁的y坐标小
        */
        if (points[i].y == Ymin.y)
        {
            if (points[i].x < Ymin.x)
            {
                Ymin.x = points[i].x;
                Ymin.y = points[i].y;
                k = i;
            }
        }
    }
    //将y坐标最小的元素与points[0]替换
    swap(0, k);
    //求其余顶点与y坐标最小的点间的直线与x轴的夹角
    for (int i = 1; i < PointsNum; i++)
    {
        /**
         * 求该直线的斜率
         * 由于points[i].x - points[0].x可能小于0，
         * 所以取绝对值
         */
        double t = (points[i].y - points[0].y) / abs(points[i].x - points[0].x);
        //通过反正切函数求得角度
        points[i].angle = atan(t);
    }
    //根据角度进行快速排序
    quickSort(1, PointsNum - 1);

    int bot = PointsNum - 1;
    int top = PointsNum;
    index[top++] = 0;//index[PointsNum]=0;
    index[top++] = 1;//index[PointsNum+1]=1;top=PointsNum+2;
    int i;
    for (i = 2; i < PointsNum; i++)
    {
        /**
         *寻找第3个点
         * 判断points[0]，points[1],points[2]三点是否共线
         */
        if (isLeft(points[index[top - 2]], points[index[top - 1]], points[i]) != 0)
        {
            break;
        }
        //如果共线就更换顶点
        index[top - 1] = i;
    }
    index[bot--] = i;//index[PointsNum-1]=i;bot=PointsNum - 2;
    index[top++] = i;//index[PointsNum+2]=i;top=PointsNum+3;

    //第一次运行
    int t;
    if (isLeft(points[index[PointsNum]], points[index[PointsNum + 1]], points[index[PointsNum + 2]]) < 0)
    {
        //检测这三个点是否为逆时针方向，如果不是，则调换位置
        t = index[PointsNum];
        index[PointsNum] = index[PointsNum + 1];
        index[PointsNum + 1] = t;
    }

    for (i++; i < PointsNum; i++)
    {	//如果成立，则说明i在凸包内，跳过
        //此时top=PointsNum+3，bot=PointsNum - 1
        if (isLeft(points[index[top - 2]], points[index[top - 1]], points[i]) > 0 && isLeft(points[index[bot + 1]], points[index[bot + 2]], points[i]) > 0)
            continue;
        //非左转，退栈
        while (isLeft(points[index[top - 2]], points[index[top - 1]], points[i]) <= 0)
            top--;
        index[top++] = i;

        //非左转，退栈
        while (isLeft(points[index[bot + 1]], points[index[bot + 2]], points[i]) <= 0)
            bot++;
        index[bot--] = i;
    }
    //在index数组里，bot+1到top-1内的就是凸包的点集
    int index1 = 0;
    for (i = bot + 1; i < top - 1; i++)
    {
        results[index1++] = points[index[i]];
        cout << points[index[i]].x << " " << points[index[i]].y << endl;
    }
}





int main()
{
    int len = readData("./points5.txt");
    getResults(points, PointsNum);
    cout << "-------------------------------------------------" << endl;
    for (int i = 0; i < PointsNum; i++)
        cout << points[i].x << " " << points[i].y << endl;
    return 0;
}

---

参考文献：

[1]凸包算法剖析[EB/OL]. /2021-01-29. https://cyw3.github.io/YalesonChan/2016/ConvexHull.html.
[2]陈道蓄. 平面上的凸包计算[J]. 中国信息技术教育, 2020(21): 25–29.