08_杨辉三角

118. 杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

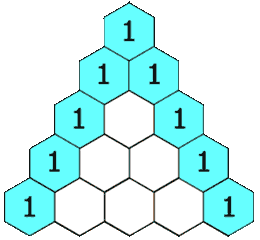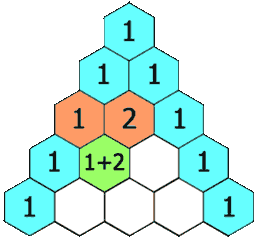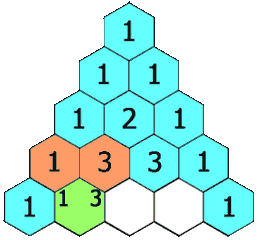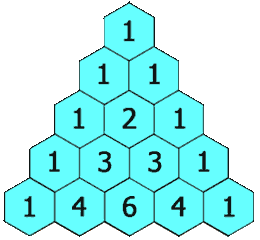
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

• 1 <= numRows <= 30

【思路】

1、dp数组的含义

dp:定义状态dp[i][j]为杨辉三角中第i行第j列（行索引从0开始）的元素值。

2、递推公式

dp[i][j] = dp[i-1][j-1] + dp[i-1][j]；

3、初始化dp数组

每一行第一个元素和最后一个元素都是1，即当i = 0或j=i时，dp[i][j]=1。

4、确定遍历顺序

5、打印dp数组

public class Solution {
	public List<List<Integer>> generate(int numRows) {
		//初始化动态规划数组
		Integer[][] dp = new Integer[numRows][];
		//遍历每一行
		for (int i = 0; i < numRows; i++) {
			//初始化当前行
			dp[i] = new Integer[i + 1];
			//每一行的第一个和最后一个元素为1；
			dp[i][0] = dp[i][i] = 1;
			//计算中间元素
			for (int j = 1; j < i; j ++) {
				//中间元素等于上一行的相邻两个元素之和
				dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
			}
		} 
		//将动态规划数组转换为结构列表
		List<List<Integer>> result = new ArrayList<List<Integer>>();
		for (Integer[] row: dp) {
			result.add(Arrays.asList(row));
		}
		//返回结果列表
		return result;
	}
}