30_删除二叉搜索树中的节点

450.删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

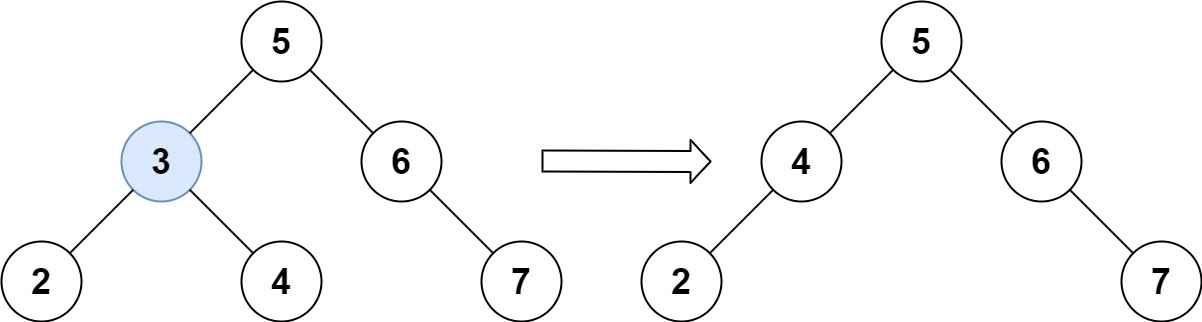
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

递归法

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        //当前节点不存在，找不到key，直接返回null
        if (root == null)
            return null;
        if (root.val == key) {  //找到了待删除的节点的值
            //情形一：待删除节点的左右孩子都为null，这一层直接返回null
            if (root.left == null && root.right == null) {
                return null;
            //情形二：待删除节点的左孩子不为null，右孩子为null,这一层直接返回root.left
            } else if (root.left != null && root.right ==null) {
                return root.left;
            //情形三：待删除节点的左孩子为null，右孩子不为null,这一层直接返回root.right
            }  else if (root.left == null && root.right != null) {
                return root.right;
            } else {
                //情形四：待删除节点的左右孩子都不为空，让右孩子作为新的根节点，让右孩子的最左下的节点指向root.left（待删除节点的左子树）
                TreeNode cur = root.right;
                while (cur.left != null) {
                    cur = cur.left;
                }
                cur.left = root.left;
                //这里是返回原来待删除节点的右孩子节点,而不是cur，cur在遍历过程中已经变了
                return root.right;
            }
        }
        if (root.val < key) root.right = deleteNode(root.right, key);
        if (root.val > key) root.left = deleteNode(root.left, key);
        return root;
    }
}