24_二叉搜索树中的搜索

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

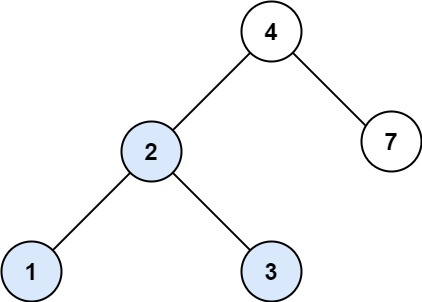
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

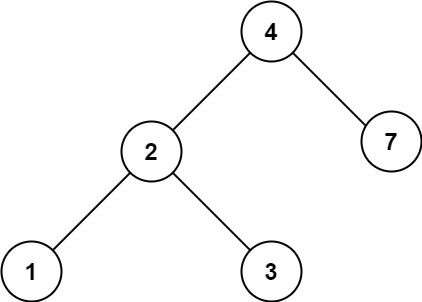
输入：root = [4,2,7,1,3], val = 5
输出：[]

【思路】

二叉搜索树是一个有序树：

• 若它的左子树不空，则左子树上所有节点的值小于它的根节点的值；
• 若它的右子树不空，则右子树上所有节点的值大于它的根节点的值；
• 它的左、右子树也分别是一颗二叉搜索树

递归法

1、确定递归函数的参数和返回值

递归函数的参数传入的是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。

TreeNode searchBST(TreeNode root, int val);

2、确定终止条件

如果root为空，或者找到了这个数值了，就返回root节点。

if (root == null || root.val == val)  return root;

3、确定单层递归的逻辑

TreeNode result = null;
if (root.val < val) result = searchBST(root.right, val);
if (root.val > val) rersult = searchBST(root.left, val);
return result;

整体代码如下：

class Solution {
    // 递归，利用二叉搜索树特点，优化
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        if (val < root.val) {
            return searchBST(root.left, val);
        } else {
            return searchBST(root.right, val);
        }
    }
}

迭代法

一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。

对于二叉搜索树是不一样的，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要掉头，在走右分支。

而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。

class Solution {
	TreeNode searchBST(TreeNode root, int val) {
        while (root != null) {
            if (root.val > val) root = root.left;
            else if (root.val < val) root = root.right;
            else return root;
        }
        return null;
    }
}

总结

本篇我们介绍了二叉搜索树的遍历方式，因为二叉搜索树的有序性，遍历的时候要比普通二叉树简单很多。

但是一些同学很容易忽略二叉搜索树的特性，所以写出遍历的代码就未必真的简单了。

所以针对二叉搜索树的题目，一样要利用其特性。

文中我依然给出递归和迭代两种方式，可以看出写法都非常简单，就是利用了二叉搜索树有序的特点。