21_从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

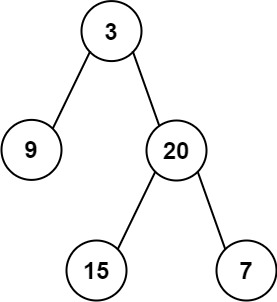
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

【思路】

首先回忆一下如何根据两个顺序构造一个唯一的二叉树，就是以后续数组的最后一个元素作为切割点，先切分中序数组，根据中序数组，反过来切分后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

说到一层一层切割，就应该使用递归来做。

• 第一步：如果数组大小为0的话，说明是空节点了
• 第二步：如果不为空，那么取后续数组最后一个元素作为节点元素
• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
• 第四步：切割中序数组，切成中序左数组和中序右数组
• 第五步：切割后序数组，切成后序左数组和后序右数组
• 第六步：递归处理左区间和右区间

TreeNode traversal(int[] inorder, int[] postorder) {
    // 第一步
    if (postorder.size() == 0) 
        return null;
    // 第二步：后序遍历数组最后一个元素，就是当前的中间节点
    int rootValue = postorder[postorder.size() - 1];
    TreeNode root = new TreeNode(rootValue);
    
    // 叶子节点
 	if (postorder.size() == 1) return root;
    
    //第三步：找到切割点
    int delimiterIndex;
    for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
        if (inorder[delimiterIndex] == rootValue) break;
    }
    // 第四步：切割中序数组，得到中序左数组和中序右数组
    // 第五步：切割后序数组，得到后序左数组和后序右数组
    //第六步
    root.left = traversal(中序左数组，后序左数组);
    root.right = traversal(中序右数组，后序右数组);
    return root;
}

综合版本

class Solution {
    Map<Integer, Integer> map;  // 方便根据数值查找位置
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
            map.put(inorder[i], i);
        }

        return findNode(inorder,  0, inorder.length, postorder,0, postorder.length);  // 前闭后开
    }

    public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
        // 参数里的范围都是前闭后开
        if (inBegin >= inEnd || postBegin >= postEnd) {  // 不满足左闭右开，说明没有元素，返回空树
            return null;
        }
        int rootIndex = map.get(postorder[postEnd - 1]);  // 找到后序遍历的最后一个元素在中序遍历中的位置
        TreeNode root = new TreeNode(inorder[rootIndex]);  // 构造结点
        int lenOfLeft = rootIndex - inBegin;  // 保存中序左子树个数，用来确定后序数列的个数
        root.left = findNode(inorder, inBegin, rootIndex,
                            postorder, postBegin, postBegin + lenOfLeft);
        root.right = findNode(inorder, rootIndex + 1, inEnd,
                            postorder, postBegin + lenOfLeft, postEnd - 1);

        return root;
    }
}

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(postorder.length == 0 || inorder.length == 0)
            return null;
        return buildHelper(inorder, 0, inorder.length, postorder, 0, postorder.length);
    
    }
    private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd){
        if(postorderStart == postorderEnd)
            return null;
        int rootVal = postorder[postorderEnd - 1];
        TreeNode root = new TreeNode(rootVal);
        int middleIndex;
        // 中序遍历找到对应的根节点
        for (middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++){
            if(inorder[middleIndex] == rootVal)
                break;
        }

        int leftInorderStart = inorderStart; //中序左子树开始下标
        int leftInorderEnd = middleIndex; // 根节点的下标 
        int rightInorderStart = middleIndex + 1; //  中序右子树的开始下标
        int rightInorderEnd = inorderEnd;  //  中序结束的下标


        int leftPostorderStart = postorderStart;  // 后序左子树的开始下标
        int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);  // 后序左子树的结束下标，需要通过中序得到的middleIndex的下标来辅助计算
        int rightPostorderStart = leftPostorderEnd;  // 后序右子树的开始下标
        int rightPostorderEnd = postorderEnd - 1;  // 后序右子树的结束下标
        root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd,  postorder, leftPostorderStart, leftPostorderEnd);
        root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd, postorder, rightPostorderStart, rightPostorderEnd);
        return root;
    }  
}