18_左叶子之和

左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

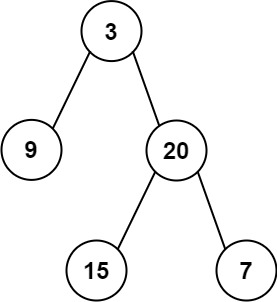
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

【思路】

首先要注意是判断左叶子，不是二叉树左侧节点，所以无法使用层序遍历。

左叶子的明确定义：节点A的左孩子不为空，且做孩子的左右孩子都为空，且做孩子的左右孩子都为空（说明是叶子结点），那么A节点的做孩子为左叶子节点，那么A的左孩子为左叶子节点。

判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，代码判断如下：

if (node.left != null && node.left.left == null && node.left,right == null) {
	// 左叶子节点处理逻辑
}

递归法

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。

递归三部曲：

1、确定递归函数的参数和返回值

​ 判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int

2、确定递归终止条件

如果遍历到空节点，那么左叶子值一定是0

if (root == null)  return 0;

注意：只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。所以如果当前遍历的节点是叶子结点，那么其左叶子也必定是0，那么终止条件为：

if (root == null)   return 0;
if (root.left == null && root.right == null)  return 0;//其实这个也可以不写，如果不写不影响结果，但就会让递归多进行了一层。

3、确定单层递归的逻辑

当遇到左叶子节点的时候，记录数值。然后通过递归求取左子树左叶子之和和右子树左叶子之和，相加便是整个树的左叶子之和。

int leftValue = sumOfLeftLeaves(root.left);  //左
if (root.left && !root.left.left && !root.left.right) {
	leftValue = root.left.val;
}
int right = sumOfLeftLeaves(root.right);  //右
int sum = leftValue + rightValue;  //中
return sum;

简化版本：

class Solution {
	public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        int leftValue = sumOfLeftLeaves(root.left);    // 左
        int rightValue = sumOfLeftLeaves(root.right);  // 右
                                                       
        int midValue = 0;
        if (root.left != null && root.left.left == null && root.left.right == null) { 
            midValue = root.left.val;
        }
        int sum = midValue + leftValue + rightValue;  // 中
        return sum;
    }
}

迭代法

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        Stack<TreeNode> stack = new Stack<> ();
        stack.add(root);
        int result = 0;
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node.left != null && node.left.left == null && node.left.right == null) {
                result += node.left.val;
            }
            if (node.right != null) stack.add(node.right);
            if (node.left != null) stack.add(node.left);
        }
        return result;
    }
}

总结

这道题目要求左叶子之和，其实是比较绕的，因为不能判断本节点是不是左叶子节点。

此时就要通过节点的父节点来判断其左孩子是不是左叶子了。

平时我们解二叉树的题目时，已经习惯了通过节点的左右孩子判断本节点的属性，而本题我们要通过节点的父节点判断本节点的属性。

希望通过这道题目，可以扩展大家对二叉树的解题思路。