06_用栈来求解汉诺塔问题
汉诺塔问题
【题目】
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
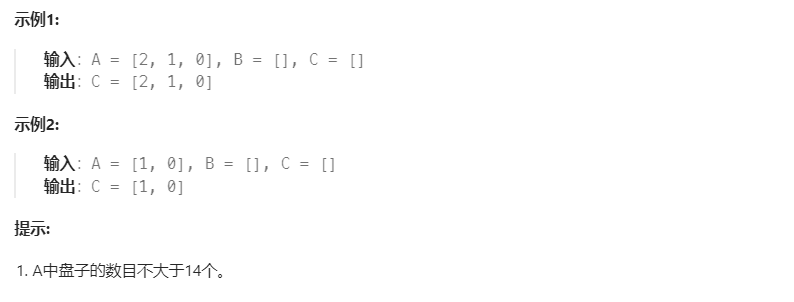
采用递归的思路 三要素如下:
递归结束条件:只剩下最后一个盘子需要移动
递归函数主要功能:
- 首先将n-1个盘子,从第一个柱子移动到第二个柱子
- 然后将最后一个盘子移动到第三个柱子上
- 最后将第二个柱子上的n-1个盘子,移动到第三个柱子上
函数的等价关系式:f(n, A, B, C)表示将n个盘子从A移动到C
f(n, A, B, C) = f(n-1,A, C, B) + f(1,A, B, C) + f(n-1, B, A, C)
class Solution {
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
moveplant(A.size(), A, B, C);
}
//size 需要移动的盘子的数量
//start 其实的柱子
//auxuliary 辅助的柱子
//target 目标柱子
public void moveplant(int size, List<Integer> start, List<Integer> auxiliary, List<Integer> target) {
//当start中只有1个盘子的时候,直接将它从第一个柱子移动到第三个柱子上
if (size == 1) {
target.add(start.remove(start.size() - 1));
return;
}
//首先将n-1个盘子,从第1个柱子移动到第2个柱子
moveplant(size - 1, start, target, auxiliary);
//然后将最后一个盘子移动到第3个柱子上
target.add(start.remove(start.size() - 1));
//最后将第二个柱子上的n-1个盘子,移动到第三个柱子上
moveplant(size - 1, auxiliary, start, target);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号