笔记：C++五一学习-分治

今天是五一，晚上学C++分治算法

1、二分查找

二分查找跨度大，速度快，枚举的跨度为1，所以慢
二分是折半的，速度logn，非常快，基础代码如下
参数aTarget是目标数，aData是数列，n是数组长度
如果按照枚举的方法，是这样的：

bool Search(int aTarget, int aData[], int n)
{
	for (int i = 0; i < n; i++)
		if (aData[i] == aTarget)
			return true;
	return false;
}

这样对于小范围的数据是可以处理的
但是：如果要遍历两亿个数呢？而且碰巧要找到的数是两亿减一的数呢？😱

---

于是二分查找出现了！😇
数组方法如下：

bool binarySearch(int aTarget, int aData[], int n)
{
	int left = 0, right = n - 1;
	while (left <= right)
	{
		mid = (left + right) / 2;
		if (aData[mid] == aTarget)
			return true;
		else if (aData[mid] < aTarget)
			left = mid + 1;
		else
			right = mid - 1;
	}
	return false;
}

换成动态数组更简单了

bool binarySearch(int aTarget, vector<int> aData)
{
	int left = 0, right = aData.size();
	while (left <= right)
	{
		mid = (left + right) / 2;
		if (aData[mid] == aTarget)
			return true;
		else if (aData[mid] < aTarget)
			left = mid + 1;
		else
			right = mid - 1;
	}
	return false;
}

最简单的还是algorithm库中的函数，直接给图

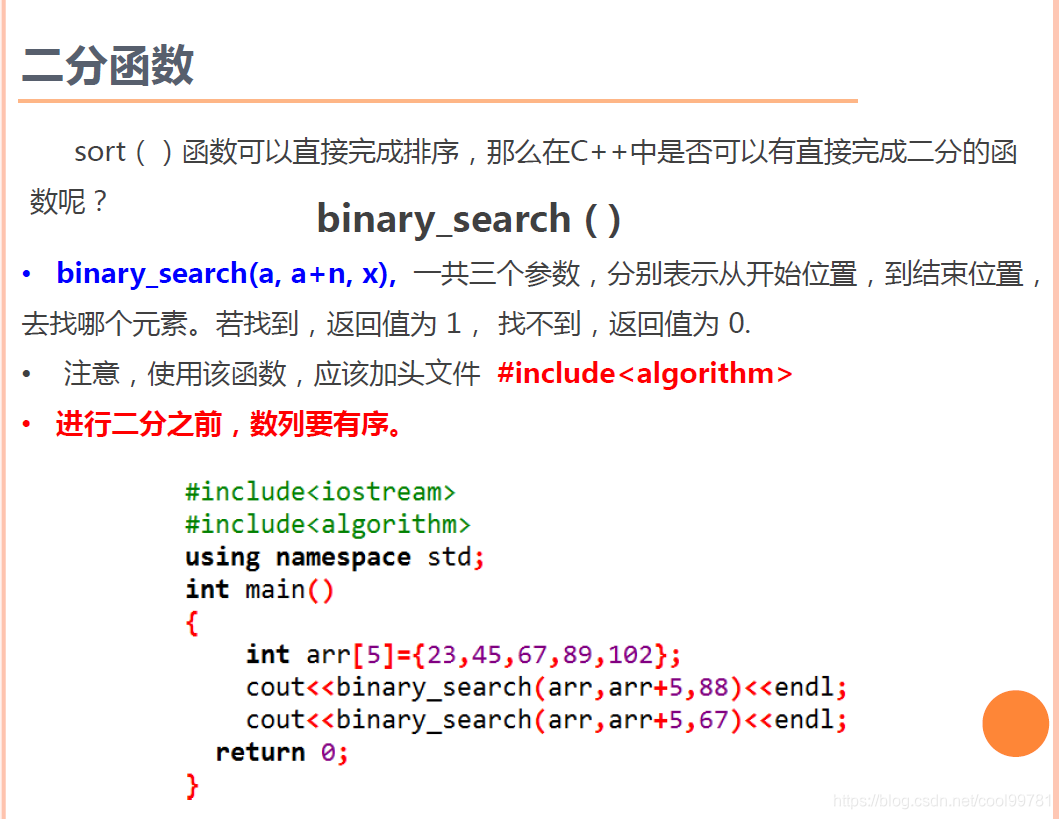
1、1二分查找练习题-砍树

这个题目用枚举显然不行，于是二分查找又伟大的出现了！
其实很简单

#include <iostream>
#include <algorithm>
#include <vector>
#include <cstdio>
using namespace std;
int main()
{
	vector<int>trees;
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < n; i++)
	{
		int tmp;
		cin >> tmp;
		trees.push_back(tmp);
	}
	sort(trees.begin(), trees.end());
	//inend
	printf("trees[trees.size() - 1] = %d\n", trees[trees.size() - 1]);
	int left = 1, right = trees[trees.size() - 1];
	int ans;
	printf("----\n");
	while (left <= right)
	{
		int all = 0;
		int mid = (left + right) / 2;
		printf("left = %d, right = %d, mid = %d\n", left, right, mid);
		for (int i = 0; i < trees.size(); i++)
			if (trees[i] - mid < 0)
				all += 0;
			else
				all += trees[i] - mid;
		cout << "all:" << all << endl;
		if (all < m)
			left = mid + 1;
		else
			right = mid - 1;
		ans = all;
	}
	cout << ans << endl;
	return 0;
}

2、快速排序

这是一个经典的分治，我有一个动图来演示！
它的基本原理是基准数

给一个快速排序的地址：https://www.jianshu.com/p/497b8ee8b517
整个排序算法专栏：https://www.jianshu.com/c/0b8a16f39eab

归并排序也是基于分治的思想，不过归并流程是将子集合合并成为有序的集合，递归执行来完成整个集合的排序。快速排序的分治流程是根据选定元素，将集合分隔为两个子集合，一个子集合中所有元素不大于选定元素值，另一个子集合中所有元素不小于选定元素值，则用于拆分集合的选定元素即为已排序元素。即每次拆分都会形成一个已排序元素，所以 个元素的序列，拆分的次数级别为O(N)。将拆分过程类比为二叉树形式，考虑普通二叉树和斜树的情况，则二叉树高度级别为O(log₂N)~O(N)。

---

作者：zhipingChen
链接：https://www.jianshu.com/p/497b8ee8b517
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

---

实现！
迭代法

typedef struct _Range {
    int start, end;
} Range;
Range new_Range(int s, int e) {
    Range r;
    r.start = s;
    r.end = e;
    return r;
}
void swap(int *x, int *y) {
    int t = *x;
    *x = *y;
    *y = t;
}
void quick_sort(int arr[], const int len) {
    if (len <= 0)
        return; // 避免len等於負值時引發段錯誤（Segment Fault）
    // r[]模擬列表,p為數量,r[p++]為push,r[--p]為pop且取得元素
    Range r[len];
    int p = 0;
    r[p++] = new_Range(0, len - 1);
    while (p) {
        Range range = r[--p];
        if (range.start >= range.end)
            continue;
        int mid = arr[(range.start + range.end) / 2]; // 選取中間點為基準點
        int left = range.start, right = range.end;
        do
        {
            while (arr[left] < mid) ++left;   // 檢測基準點左側是否符合要求
            while (arr[right] > mid) --right; //檢測基準點右側是否符合要求
 
            if (left <= right)
            {
                swap(&arr[left],&arr[right]);
                left++;right--;               // 移動指針以繼續
            }
        } while (left <= right);
 
        if (range.start < right) r[p++] = new_Range(range.start, right);
        if (range.end > left) r[p++] = new_Range(left, range.end);
    }
}

递归法

void swap(int *x, int *y) {
    int t = *x;
    *x = *y;
    *y = t;
}
void quick_sort_recursive(int arr[], int start, int end) {
    if (start >= end)
        return;
    int mid = arr[end];
    int left = start, right = end - 1;
    while (left < right) {
        while (arr[left] < mid && left < right)
            left++;
        while (arr[right] >= mid && left < right)
            right--;
        swap(&arr[left], &arr[right]);
    }
    if (arr[left] >= arr[end])
        swap(&arr[left], &arr[end]);
    else
        left++;
    if (left)
        quick_sort_recursive(arr, start, left - 1);
    quick_sort_recursive(arr, left + 1, end);
}
void quick_sort(int arr[], int len) {
    quick_sort_recursive(arr, 0, len - 1);
}