day16 || lc513. 找树左下角的值 || lc112.路径总和 || lc106从中序和后续便利构造二叉树 || lc105_前序和中序构造二叉树

day16

lc513. 找树左下角的值

给定一个二叉树，在树的最后一行找到最左边的值。

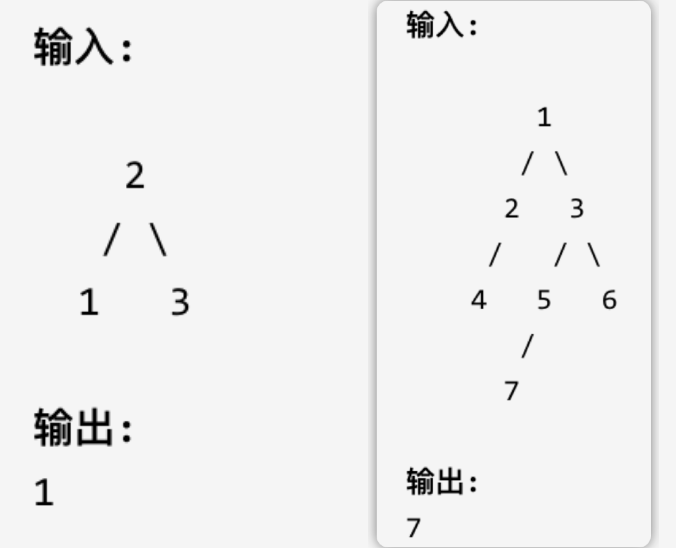
树的最后一行 的 最左值

怎么找左下角呢?

只需要求深度最大的叶子节点 那么一定是最后一行 找到最后一行之后 使用前序便利 只要能保证左边优先进行搜索就行 然后记录最大的叶子节点 此时就是树的最后以后最左位置

递归法

class Solution {
    int Deep = -1, value = 0;
    public int findBottomLeftValue(TreeNode root) {
        value = root.val;
        findLeft(root ,0);
        return value;
        
    }
    public void findLeft(TreeNode root, int d){
        if(root == null) return;
        if(root.left == null && root.right == null){
            if(d > Deep){
                value = root.val;
                Deep = d;
            }
        }
        if(root.left != null) findLeft(root.left, d + 1);
        if(root.right != null) findLeft(root.right, d + 1);
    }
}

迭代法

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        int res = 0;
        while(!q.isEmpty()){
            int size = q.size();
            for(int i = 0; i < size; i++){
                TreeNode poll = q.poll();
                if(i == 0) res = poll.val;
                if(poll.left != null) q.offer(poll.left);
                if(poll.right != null) q.offer(poll.right);
            }
        }
        
      return res;

    }
}

lc112.路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

给定如下二叉树，以及目标和 sum = 22

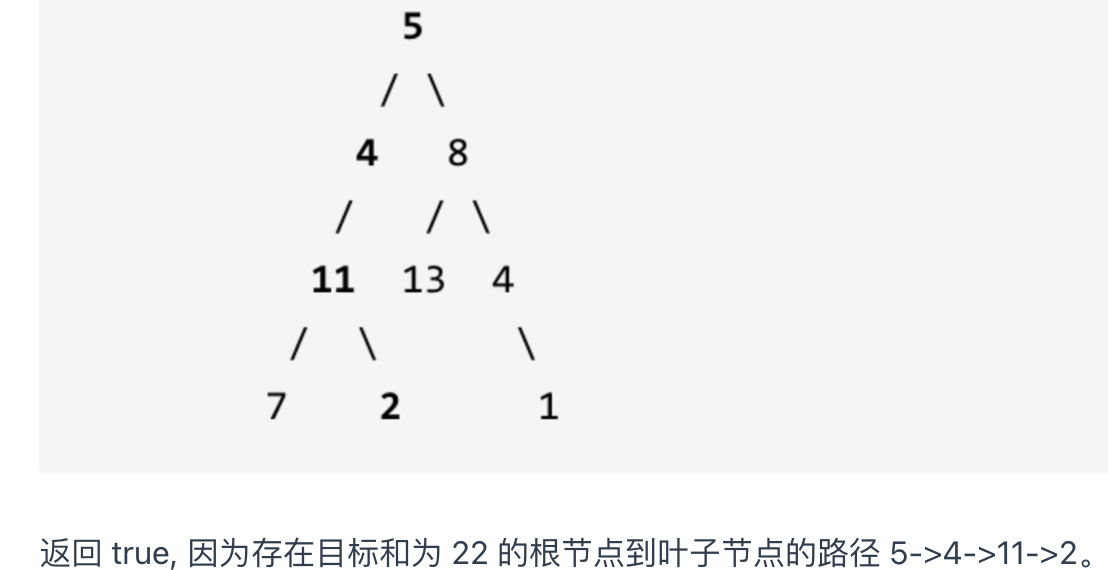
注意: 是根节点到叶子结点的路径 只要有一条符合 那就是true

只要看到二叉树 就要想便利顺序 本题任何顺序都可以 因为不涉及根节点的处理逻辑 根节点放在哪里都可以

---

递归三部曲

1. **确定返回值和参数 **

返回boolean类型 只要有符合的就返回 参数是跟节点root , 计数器int count ,这里直接传入目标值, 遇到一个节点就把节点数值做减法操作, 如果到叶子节点 count等于0了 说明符合

2. 终止条件

如果跟是null 那直接返回false

遇到叶子节点 判断 左右孩子都是空 并且count等于0 就终止 return true

如果遇到叶子了 但是count不等于0 那说明不是符合的路径 return false;

3. 单层递归的逻辑

向左便利 把目标值做减法 然后左递归

本题递归函数返回类型是Boolean 如果左方向返回true就符合继续return true

但是递归返回false说明不符合 那就回退回溯 回溯就把值加回来 然后向右便利递归

向右的逻辑和向左的一样 如果依然没有返回true 说明整个都不符合

综上: 只有左便利 右便利

---

public boolean hasPathSum(Node root, int targetSum) {

    if(root == null) return false;  //空的直接返回false
    targetSum -= root.val;    // 做减法 
    if(root.l == null && root.r == null) return targetSum == 0;  

    if(root.l != null){
        boolean lv = hasPathSum(root.l, targetSum);
        if(lv) return true;
    }

    if(root.l != null){
        boolean rv = hasPathSum(root.r, targetSum);
        if(rv) return true;
    }
    return false;

}

为什么刚刚提到了回溯要加回来 但是代码没有写出呢?

因为java中 基本数据类型是按值传递的, , 所以原始值不会变化

---

lc106从中序和后续便利构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。 --- 中等

注意: 你可以假设树中没有重复的元素。

前序: 跟 左 右 中序: 左 跟 右 后序: 左 右 跟

---

中序是 9 3 15 20 7

后续是 9 15 7 20 3

1. 找根节点

根据便利顺序 中序是左根右 后续是左右跟 后续的最后一个节点是跟 得出根节点是3

2. 有跟之后看中序得出左右

找到根节点是3 那么看中序 根节点的前面就是左节点 也就是9 右节点是 15 20 7

3. 再看后续得孩子顺序

在后续剩余的是15 7 20 这三个 后续最后节点是跟 也就是20 是跟

4. 再去看中序

最后的三个在中序的顺序是 15 20 7 已经找到20是跟 那么 15是左 7是右

** 3**

** / **

** 9 20**

** / **

** 15 7**

---

综上: 在代码顺序为

1. 后序数组为0的话 说明是空节点
2. 找根 后序数组最后一个元素
3. 寻找中序数组跟的位置作为切割点
4. 切割中序数组 得出左右子树
5. 切割后续
6. 递归处理左右区间

---

然后递归三部曲

1. 返回类型是 根据中和后构造二叉树的节点 参数是两个数组
2. 后续数组为0 说明是空节点 return null
3. 单层处理逻辑

• 后续数组的最后一个元素就是根节点 构造出根节点
• 找出根节点在中序数组的位置 int i = 0; for(i = 0; i < 中序长度; i++ ) if(中[i] == rootV) break; 此时break之后只留下i 也就是根节点在中序数组的下标位置
• 使用上一步的 i 切割中序 得出左右子树
• 使用中序数组左区间大小 切后续的左区间

注意:

在切割中序数组 以及后续数组 注意区间

切割中序 使用i 也就是后序数组最后一个元素根节点在中序的位置

切中序 使用的是中序数组的左区间大小 切 后续的左区间

public class Lc106_buildTree {

    Map<Integer, Integer> m;  //用来快速定位中序遍历中节点的索引位置。

    public Node buildTree(int[] in, int[] post) {
        m = new HashMap<>();

        //用map保存中序序列的数值对应的位置
        for(int i = 0; i < in.length; i++) m.put(in[i], i);

        return findNode(in, 0, in.length, post, 0, post.length);

    }

    public Node findNode(int[] in, int inBegin, int inEnd, int[] post, int postBegin, int postEnd) {
        //左闭右开  如果不满足 说明是空的
        if(inBegin >= inEnd || postBegin >= postEnd) return null;
        // 后续数组的最后一个元素 就是根节点 然后构造出来
        int rootIndex = m.get(post[postEnd - 1]);
        Node root = new Node(in[rootIndex]);
        // 保存中序的左子树个数, 确定后续数组的个数
        int lLength = rootIndex - inBegin;

        root.l = findNode(in, inBegin, rootIndex, post, postBegin, postBegin + lLength);

        root.r = findNode(in, rootIndex + 1, inEnd, post, postBegin + lLength, postEnd - 1);

        return root;
    }
}

注意本题的左右子树在中序和后序中的区间：

- **左子树：**
    * 中序区间：`[inBegin, rootIndex)`
    * 后序区间：`[postBegin, postBegin + lLength)`
- **右子树：**
    * 中序区间：`[rootIndex + 1, inEnd)`
    * 后序区间：`[postBegin + lLength, postEnd - 1)`

---

lc105_知道前序和中序构造二叉树

那么前序和中序能够构造二叉树吗?

前是跟左右 中是左跟右

根据前序数组 第一个就是根节点

/**
 * lc105_找到前序和中序 还原二叉树 返回根节点
 */
public class Lc105_buildTreeQz {

    Map<Integer, Integer> m;

    public Node buildTree(int[] pre, int[] mid) {
        m = new HashMap<>();

        for(int i = 0; i < mid.length; i++) m.put(mid[i],i);

        return findNodeII(pre,0,pre.length,mid,0,mid.length);

    }

    private Node findNodeII(int[] pre, int preB, int preE, int[] mid, int midB, int midE) {
        if(preB >= preE || midB >= midE) return null;

        int rootIndex = m.get(pre[preB]);
        Node root = new Node(mid[rootIndex]);

        int lLen = rootIndex - midB;

        root.l = findNodeII(pre, preB + 1,preB + lLen + 1, mid, midB, rootIndex);

        root.r = findNodeII(pre, preB + lLen + 1, preE, mid, rootIndex + 1, midE);

        return root;

    }
}

**但是知道后续和前序 不能构造二叉树 因为 后续是左右跟 可以得出跟在哪 前序是跟左右 **

关键是这俩左右是挨一块的 所以没办法分割区间

---