线段树基础设计的个人理解
概述
线段树是一棵二叉搜索树, 每个树节点代表一个线段或者说一个区间范围, 常用于解决各种区间修改、区间查询问题, 本文暂时只讲述基础概念, 用经典的区间最值问题作为示例。
数据结构
经典代码模板都是用数组来实现线段树, 按照层序遍历的顺序给每个节点分配数组空间, 从根节点代表的完整区间开始逐层二分出左孩子节点\([left, mid]\)和右孩子节点\([mid+1, right]\), 直到最终叶子节点代表长度仅为1的单点区间。
为了方便求出子节点在数组中的下标, 根节点从数组下标1位置开始, 容易推论出下标i位置节点的左右孩子下标分别为 \(i*2\) 和 \(i*2+1\), 代码里一般通过位运算 \(i << 1 | 1\) 快速求出。
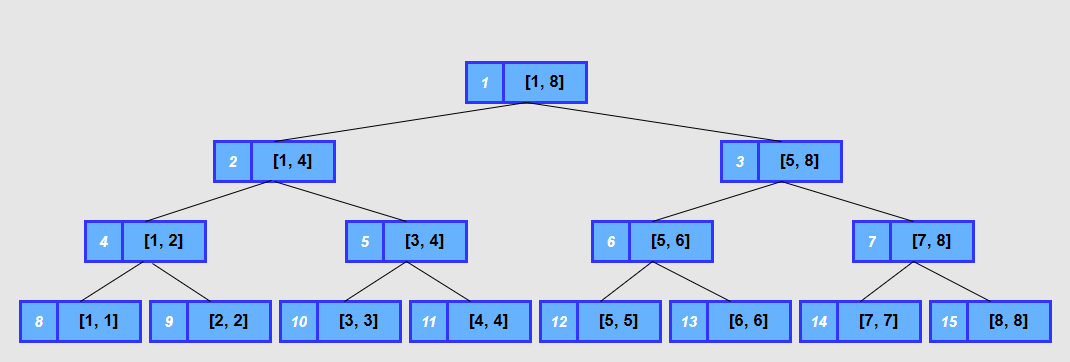
下图是以8个数字的区间为例的树节点及对应区间和下标的信息:
复杂度分析
-
线段树每层都是通过二分区间来构建的, 所以树的高度就是\(log_2 n\)级别, 总共n个叶子节点都是从根节点向下创建, 所以构建过程的时间复杂度是\(O(n*log_2 n)\)。
-
根据叶子节点必须有n个来讨论线段树所需要开辟的空间:
- 空间利用率最高的情况就是n恰好等于2的整数幂时(即 \(2^{log_2 n}\) = n, 可以参考上面[1, 8]区间对应的线段树示例图), 此时叶子节点全都属于最后一层, 非叶子节点有n-1个, 再加上下标0舍弃不用, 总共需要\(2*n\)空间。
- 其它情况就会有部分叶子节点要在更深一层创建的, 例如[1, 3]区间的线段树左右孩子分别是[1, 2]和[3, 3], [1, 1]和[2, 2]区间叶子节点会比[3, 3]更深一层。 用数组实现的线段树, 即使最后一层有很多空节点也是需要占用额外空间, 所以肯定会浪费一些空间, 此时线段树忽略最后一层就是个满二叉树, 倒数第二层的叶子节点个数是O(n)级别所以最后一层最多需要有2n个节点空间, 从而得到线段树所需空间在[2n, 4n)范围内, 一般保险起见数组直接开辟4*n长度。
- 感兴趣的朋友可以用下面这段本人自己写的递推代码代码试试数值范围与线段树所需最大下标的对应倍数关系:
private static void maxIndex(int n) { // 总数i的线段树最大下标值为: memo[i][0] + memo[i][1], 其中memo[i][0]为最大的2的整数幂即最后一层首个节点对应下标值 int[][] memo = new int[n + 1][2]; memo[1][0] = 1; memo[1][1] = 0; double maxTime = 0.0; int maxCnt = 1; for (int i = 2; i <= n; i++) { int lCnt = (1 + i) >> 1, rCnt = i - lCnt; // 左子树的最大下标是 2 * memo[lCnt][0] + memo[lCnt][1], 右子树最大下标是 3 * memo[rCnt][0] + memo[rCnt][1] int val; if (lCnt == rCnt) { val = (memo[rCnt][0] << 1) + memo[rCnt][0] + memo[rCnt][1]; } else { val = Math.max((memo[lCnt][0] << 1) + memo[lCnt][1], (memo[rCnt][0] << 1) + memo[rCnt][0] + memo[rCnt][1]); } // 计算需要开辟的空间与i的倍数(算上空着的下标0位置) double time = (val + 1.0) / i; if (time > maxTime) { maxTime = time; maxCnt = i; } memo[i][0] = Integer.highestOneBit(val); memo[i][1] = val - memo[i][0]; System.out.println("元素个数 " + i + " 对应线段树做需要最大下标为 " + val + ", 倍数是: " + String.format("%.6f", time)); } System.out.println("最大倍数为 " + maxCnt + " 所需的 " + String.format("%.6f", maxTime)); }
代码逻辑
线段树所有代码都是从根节点逐层向下递归处理, 下面代码以同时处理区间最大值和区间累加和为例。
初始化构建
-
自顶向下从根节点代表的完整区间逐层递归创建, 递归方法参数包含区间左右边界值以及对应数组下标;
-
递归出口是区间左右边界值相等也就是长度为1的叶子节点, 线段树数组元素值就等于原数组值;
-
再自底向上逐层汇总收集父节点的区间值赋值给对应线段树数组元素, 直到根节点结束。
// 保存原数组数据的变量, 可以省略, 仅用于构建过程 private int[] arr; // 区间累加和 private int[] sum; // 区间最大值 private int[] max; // 懒标记信息 private int[] add; public SegmentTree(int[] arr) { int size = arr.length; this.arr = Arrays.copyOf(arr, arr.length); sum = new int[size << 2]; max = new int[size << 2]; add = new int[size << 2]; build(0, size - 1, 1); } /** * 构建线段树的[left, right]区间节点 * * @param i 节点在数组中所属的下标 */ public void build(int left, int right, int i) { if (left == right) { sum[i] = arr[left]; max[i] = arr[left]; } else { int mid = (left + right) >> 1; build(left, mid, i << 1); build(mid + 1, right, i << 1 | 1); up(i); } } /** * 收集左右子节点区间数据 */ private void up(int i) { sum[i] = sum[i << 1] + sum[i << 1 | 1]; max[i] = Math.max(max[i << 1], max[i << 1 | 1]); }
区间修改
-
区间修改add方法参数列表中包含待处理区间的左右边界和修改操作要统一增加的数值这三个固定参数, 再用额外三个参数表示当前处理的节点左右边界及对应下标值;
-
如果待处理区间完全覆盖当前节点区间, 直接修改当前节点对应的累加和与最大值, 同时借助懒标记信息记录本次要修改的值从而省去继续往下递归子节点的时间, 这部分懒标记信息会在需要区分处理更小的子区间数据时再下发到子节点进行处理;
-
如果不能完全覆盖, 先将当前区间可能存在的懒标记数据下发到左右孩子节点, 这个下发down方法只需要当前节点下标i以及左右孩子节点区间长度三个变量, 孩子节点接收懒标记信息后就清空当前节点的懒标记信息;
-
如果待处理区间包含左孩子节点就递归处理左孩子, 包含右孩子节点也递归处理右孩子, 处理完成后再调用构建过程使用过的up方法收集汇总到父节点中;
-
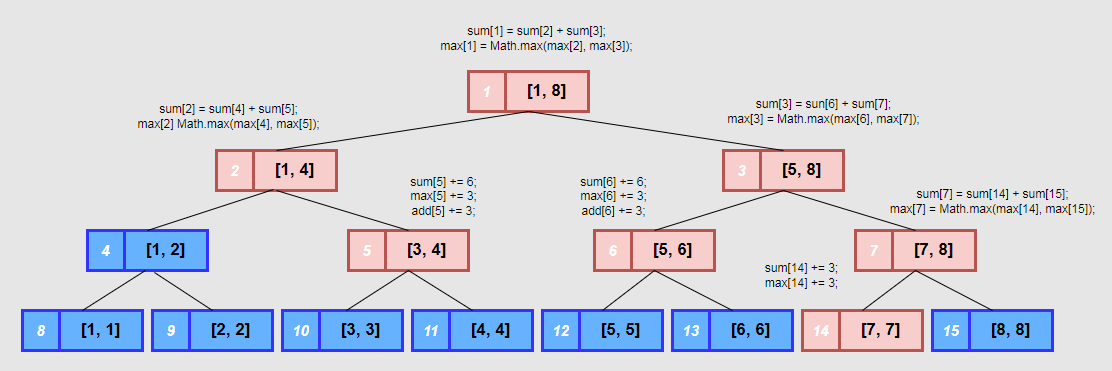
下图以在[1, 8]线段树中更新[3, 7]区间所有元素增加3为例标记了会递归处理的区间节点。 其中[3, 4]和[5, 6]节点都被待处理区间[3, 7]完全覆盖, 所以都是只更新自身节点的懒标记信息(累加和要增加3*区间长度2, 最大值和懒标记信息都增加3)后就不再继续递归到叶子节点了, 但是最深层的[7, 7]节点所有祖先节点都没被完全覆盖所以是会最终递归到。
![]()
-
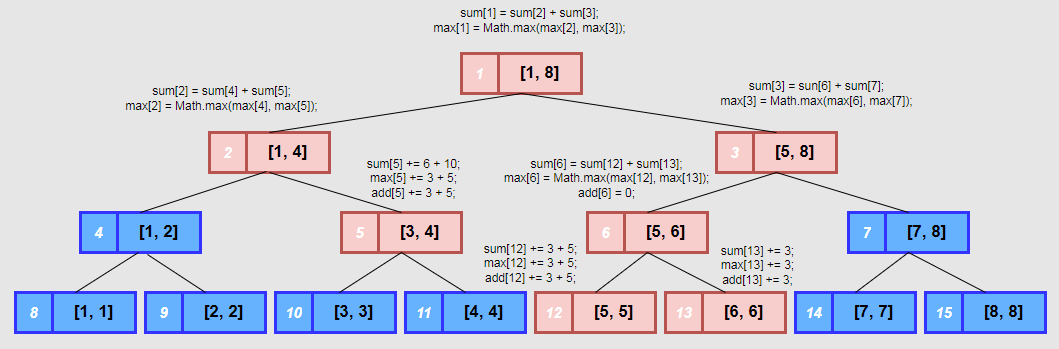
再以继续更新[3, 5]区间所有元素增加5为例, [3, 4]节点区间被完全覆盖所以仍然只更新自身节点信息不再递归孩子节点, [5, 6]区间有部分没被覆盖所以需要递归到[5, 5], 再递归之前会将上一步更新的懒标记信息先下发到两个孩子节点[5, 5]和[6, 6]中, 等到处理完[5, 5]节点后再逐层向上返回更新父节点数据。
![]()
/** * 收集左右子节点区间数据 */ private void up(int i) { sum[i] = sum[i << 1] + sum[i << 1 | 1]; max[i] = Math.max(max[i << 1], max[i << 1 | 1]); } /** * 懒信息下发 * * @param i 下标 * @param leftCnt 左孩子区间数值个数 * @param rightCnt 右孩子区间数值个数 */ private void down(int i, int leftCnt, int rightCnt) { if (add[i] == 0) { return; } lazy(i << 1, add[i], leftCnt); lazy(i << 1 | 1, add[i], rightCnt); // 下发后父节点的懒信息清空 add[i] = 0; } /** * 区间全覆盖, 节点数据与懒信息更新 * * @param i 下标 * @param val 统一要增加的值 * @param cnt 区间数值的个数 */ private void lazy(int i, int val, int cnt) { sum[i] += val * cnt; max[i] += val; add[i] += val; } /** * 在指定范围内统一增加某个值 * * @param jobL 任务需要更新的区间左边界 * @param jobR 任务需要更新的区间右边界 * @param jobV 任务需要增加的值 * @param left 节点对应的区间左边界 * @param right 节点对应的区间右边界 * @param i 节点下标 */ public void add(int jobL, int jobR, int jobV, int left, int right, int i) { if (jobL <= left && jobR >= right) { lazy(i, jobV, right - left + 1); } else { int mid = (left + right) >> 1; down(i, mid - left + 1, right - mid); if (jobL <= mid) { add(jobL, jobR, jobV, left, mid, i << 1); } if (jobR > mid) { add(jobL, jobR, jobV, mid + 1, right, i << 1 | 1); } up(i); } }
区间查询
-
查询也是从根节点递归处理, 方法参数和逻辑与修改操作基本一样;
-
如果节点区间完全被待查询区间覆盖, 直接返回当前节点数据;
-
如果不能完全覆盖, 包含左半区间就递归左孩子, 包含右半区间也递归右孩子, 汇总得到当前节点的递归返回值。
/** * 查询指定范围的数值之和 */ public int querySum(int jobL, int jobR, int left, int right, int i) { if (jobL <= left && jobR >= right) { return sum[i]; } int mid = (left + right) >> 1; down(i, mid - left + 1, right - mid); int ans = 0; if (jobL <= mid) { ans += querySum(jobL, jobR, left, mid, i << 1); } if (jobR > mid) { ans += querySum(jobL, jobR, mid + 1, right, i << 1 | 1); } return ans; } /** * 查询指定范围的最大值 */ public int queryMax(int jobL, int jobR, int left, int right, int i) { if (jobL <= left && jobR >= right) { return max[i]; } int mid = (left + right) >> 1; down(i, mid - left + 1, right - mid); int ans = 0; if (jobL <= mid) { ans = queryMax(jobL, jobR, left, mid, i << 1); } if (jobR > mid) { ans = Math.max(ans, queryMax(jobL, jobR, mid + 1, right, i << 1 | 1)); } return ans; }
本文表述基于作者主观理解,如有错漏或歧义之处,欢迎评论指出沟通交流


 浙公网安备 33010602011771号
浙公网安备 33010602011771号