【LeetCode 310】最小高度树

题目描述

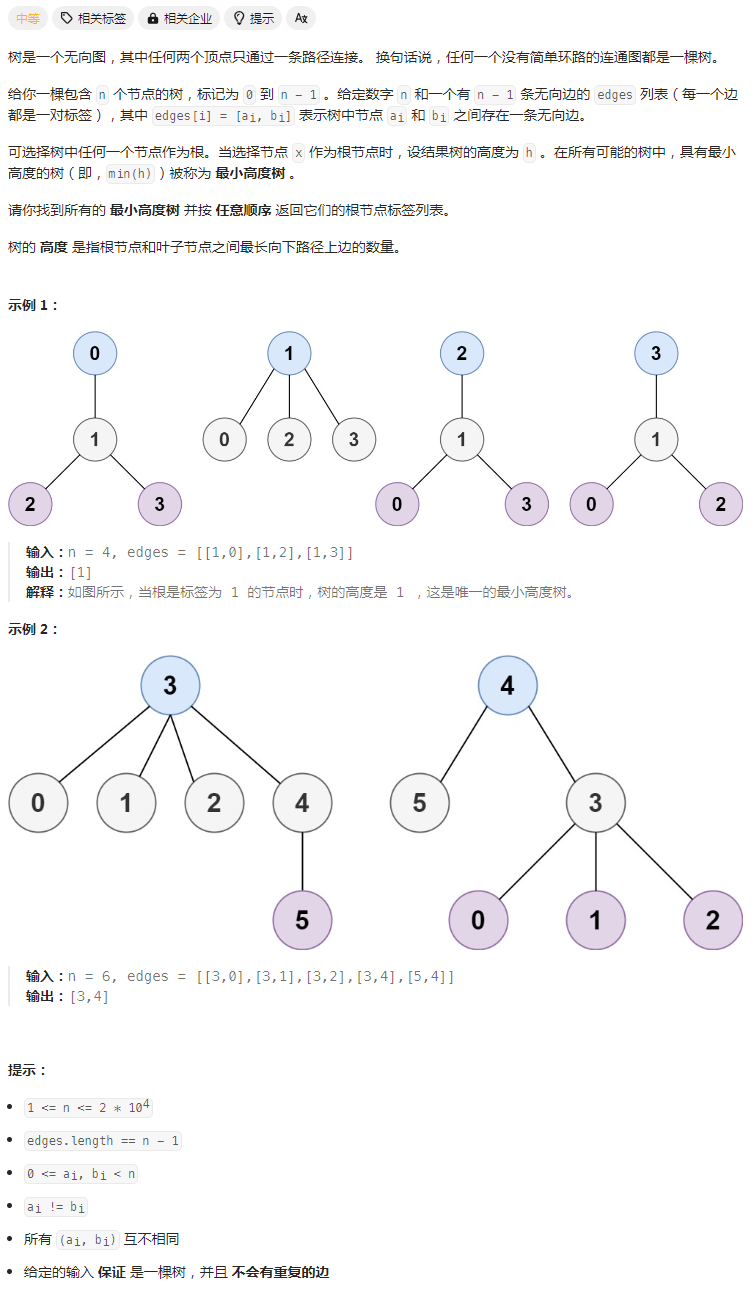
原题链接： LeetCode.310 最小高度树

解题思路

• 最小高度树的叶子节点肯定是初始只有一条边的节点；
• 广度优先遍历， 逐批将当前叶子节点移除， 再将移除后新的叶子节点入队；
• 所有节点全部入队时， 当前队列中剩余的最后一批"叶子节点"就是答案；
• 坦白说这题的严格思路证明没想过， 第一反应直接想到了解法并且提交通过， 更严谨的证明过程感兴趣再去看题解吧， 包括求树中最长路径得到答案的解法也有待了解。

解题代码

  /**
   * 拓补排序解法， 逐批移除度为1的节点， 所有节点全部入队时最后一批入队的节点就是答案
   * 执行用时： 10 ms , 在所有 Java 提交中击败了 99.15% 的用户
   * 内存消耗： 54.16 MB , 在所有 Java 提交中击败了 72.91% 的用户
   */
  public List<Integer> findMinHeightTrees(int n, int[][] edges) {
      List<Integer> ans = new ArrayList<>();
      if (n < 3) {
          for (int i = 0; i < n; i++) {
              ans.add(i);
          }
          return ans;
      }
      // 生成邻接表并统计节点的度
      List<Integer>[] graph = new List[n];
      for (int i = 0; i < n; i++) {
          graph[i] = new ArrayList<>();
      }
      int[] degree = new int[n];
      for (int[] edge : edges) {
          int u = edge[0], v = edge[1];
          graph[u].add(v);
          graph[v].add(u);
          degree[u]++;
          degree[v]++;
      }
      int[] queue = new int[n];
      int head = 0, tail = 0;
      for (int i = 0; i < n; i++) {
          if (degree[i] == 1) {
              queue[tail++] = i;
          }
      }
      while (tail > head) {
          int size = tail - head;
          while (size-- > 0) {
              int u = queue[head++];
              for (int v : graph[u]) {
                  degree[v]--;
                  if (degree[v] == 1) {
                      queue[tail++] = v;
                  }
              }
          }
          if (tail == n) {
              // 所有节点都已入队， 当前队列中所有节点的度都只剩1， 都可以作为最小高度树的根
              while (tail > head) {
                  ans.add(queue[head++]);
              }
              break;
          }
      }
      return ans;
  }