【LeetCode 1466】重新规划路线

题目描述

原题链接： LeetCode.1466 重新规划路线

解题思路

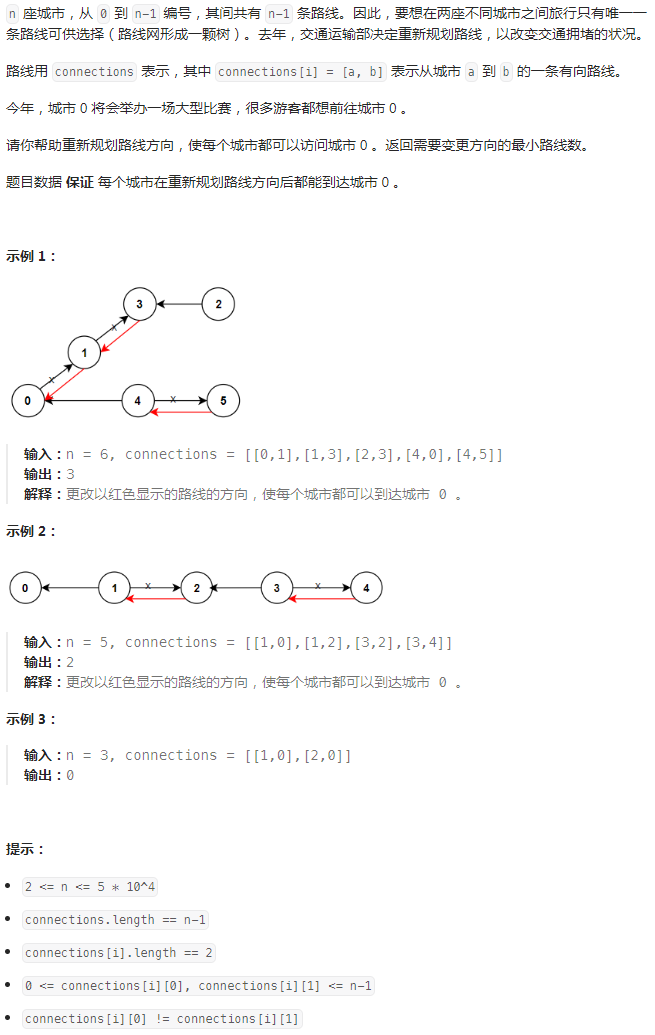
• 路线网形成一棵树， 说明每个节点都参与两条路线， 或作为起点或作为终点；
• 要想所有城市都可以通往城市0， 必须要把所有逆向的路线都变更一次方向， 逆向路线总数量即为答案；
• 朴素BFS版本
  • 从城市0出发， 遍历每个从已通城市出发的下一个城市都对应一条需要变更方向的逆向路线， 次数+1然后将归入这些新的已通城市；
  • 再遍历可前往每个已通城市为终点的城市直接纳入已通城市；
  • 直到所有城市编号都已出队， 返回统计到的次数即为答案。
• 从提交结果图中看到的版本
  • 以路线维度进行遍历， 用boolean数组表示哪些城市编号属于已通城市；
  • 每次遍历路线时， 如果终点属于已通城市那么起点也直接标记为已通城市；
  • 否则再判断起点为已通城市时就是找到了一条需要变更方向的逆向路线， 次数+1然后将终点归入已通城市；
  • 如果起点终点都不属于已通城市， 这条路线保留等待下一轮遍历；
  • 初始化时不需要关心给定的路线顺序， 进行首轮遍历后反复进行一轮轮遍历， 所有路线的起终点均属于已通城市。

解题代码

• 朴素BFS解法

    /**
     * BFS处理，数组实现队列
     * 执行用时： 34 ms , 在所有 Java 提交中击败了 58.67% 的用户
     * 内存消耗： 67.82 MB , 在所有 Java 提交中击败了 69.70% 的用户
     */
    public int minReorder(int n, int[][] connections) {
        List<Integer>[] toGraph = new List[n];
        List<Integer>[] fromGraph = new List[n];
        for (int i = 0; i < n; i++) {
            toGraph[i] = new ArrayList<>();
            fromGraph[i] = new ArrayList<>();
        }
        for (int[] con : connections) {
            toGraph[con[0]].add(con[1]);
            fromGraph[con[1]].add(con[0]);
        }
        if (toGraph[0].size() == n - 1) {
            return 0;
        }
        int cnt = 0;
        boolean[] visited = new boolean[n];
        int[] queue = new int[n];// 用ArrayDeque的执行用时要慢10ms
        int head = 0, tail = 0;
        queue[tail++] = 0;
        while (tail > head) {
            int c = queue[head++];
            visited[c] = true;
            for (int next : toGraph[c]) {
                if (!visited[next]) {
                    cnt++;
                    queue[tail++] = next;
                }
            }
            for (int pre : fromGraph[c]) {
                if (!visited[pre]) {
                    queue[tail++] = pre;
                }
            }
        }
        return cnt;
    }
  

• 以路线维度进行遍历的解法

    /**
     * 从提交结果中复制出来的代码
     * 执行用时： 4 ms , 在所有 Java 提交中击败了 98.87% 的用户
     * 内存消耗： 71.73 MB , 在所有 Java 提交中击败了 13.82% 的用户
     */
    public int minReorder(int n, int[][] connections) {
        int ans = 0;
        boolean[] canArrive = new boolean[n];
        canArrive[0] = true;
        // 记录两端城市都无法到达城市0的路线编号
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < connections.length; i++) {
            int from = connections[i][0], to = connections[i][1];
            if (canArrive[to]) {// 目的城市能到达，起始城市也可以，直接标记
                canArrive[from] = true;
            }
            else if (canArrive[from]) {// 起始城市能到达，变更方向后目的城市也能到达，次数+1后标记
                ans++;
                canArrive[to] = true;
            }
            else {// 首尾城市都不能到达，待处理
                list.add(i);
            }
        }
        while (!list.isEmpty()) {// 循环处理直到每个路线首尾两端城市全部可到达
            for (int i = list.size() - 1; i >= 0; i--) {
                int u = connections[list.get(i)][0];
                int v = connections[list.get(i)][1];
                if (canArrive[v]) {
                    canArrive[u] = true;
                    list.remove(i);
                }
                else if (canArrive[u]) {
                    ans++;
                    canArrive[v] = true;
                    list.remove(i);
                }
            }
        }
        return ans;
    }