KMP算法的证明与代码示例

KMP算法的个人理解

• 背景

  字符串查找算法的需求是：给定一个字符串S和子串P，查找P在S串中出现的位置，如果没出现过就返回-1。
  
  首先想到的暴力方法是双指针遍历匹配两个字符串中的所有字符，假设字符串S的i位与子串P的j位不匹配，将i右移一位再把j恢复到0从P的首位重新开始匹配。如果S和P字符串长度分别为m和n，暴力方法的时间复杂度就是O(m x n)，效率太低。
  
  

• 主要思路

  暴力算法效率低下的原因在于一旦匹配失败就粗暴地回撤两个字符串的匹配下标，会产生大量不必要的重复匹配工作。Knuth、Morris和Pratt三位大佬想到一种方法，在匹配过程中保证主串待比较的下标i不回退，利用已经匹配过的部分信息来加速查找过程，通过跨越找到子串P需要重新匹配的位置提升效率。
  

  1. 根据子串P生成辅助用的next数组，next[j]值的含义是[0...j-1]范围子串的前缀与后缀相同的最大长度。
  2. 主串下标i和子串下标j都从0开始匹配，字符相同时两个下标同时右移+1；匹配失败时如果子串下标是0也是将两个下标同时右移+1，如果j > 0则主串下标i先保持不变，子串下标由j变成next[j]。（稍后会详细证明为什么可以从next[j]重新匹配）
  3. 子串下标先越界说明已经找到符合要求的位置，即i - P.length()；反之如果主串下标i越界了则是未找到完全匹配的情况，返回-1作为结果。

• next数组求解与证明

  • 按定义朴素求值

    以字符串"aabat"为例，求的next数组值如下表：

    下标值	前缀集合	后缀集合	next值
    0	--	--	-1
    1	--	--	0
    2	"a"	"a"	1
    3	"a"、"aa"	"b"、"ab"	0
    4	"a"、"aa"、"aab"	"a"、"ba"、"aba"	1

    注：按照定义，next[0]显然是没有意义的可以直接赋值为-1，再需要特殊说明的是求的最大长度相同前缀和后缀是不包含整段字符串本身的，所以next[1]的值是0。

  • 借助next数组可以加速匹配的证明

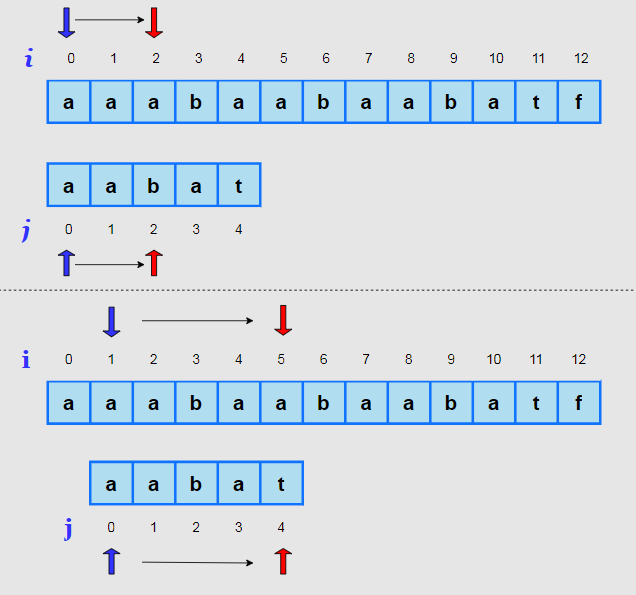
    给定当前匹配失败时字符串S和P的下标分别为i和j，next[j]值为x。

    1. S[i-j, i-1]与P[0, j-1]完全相同；
    2. P[0, x-1] == P[j - x, j-1] == S[i-j, i-j+x-1] == S[i-x, i-1]；
       
    3. 暴力解法是应该用S[i-j+1]继续和P[0]尝试匹配，KMP算法直接跳过S[i-j+1, i-x-1]这段必不可能相同的无用范围，用反证法可以证明不存在(i-j < k < i - x)能满足S[k, i-1] == P[0, i-k-1]：假设S[k, i-1] == P[0, i-k-1]，由于S[k, i-1] == P[j+k-i, j-1]，所以得到P[0, i-k-1] == P[j+k-i, j-1]，但是由next[j]=x可知P[0, j-1]不可能存在比x更大的前缀后缀匹配长度。
       
    4. 由于S[i-x, i-1] == P[0, x-1]，所以下一步j更新为next[j]即用P[x]与S[i]进行匹配等同于用S[i-x]与P[0]进行匹配，跳过了长度为x必定相同的重复匹配很好理解；
    5. 总结就是KMP算法根据next数组值先跳过第一段不可能相同的S[i-j+1, i-x-1]范围，再跳过第二段必定相同的S[i-x, i-1]范围，从而实现下标i不回退，只需要重新指定P的匹配下标就能继续下一轮匹配。

  • 快速求next数组值的步骤

    类似的，求next数组值的时候也可以借助前面已经求得的数据快速得到答案，具体逻辑如下：

    1. 求next[j]时，根据next[j-1] == x直接判断P[x]与P[j-1]是否相同，如果相同则求得next[j] = x+1；
       
    2. 如果P[x] != P[j-1]，继续判断P[next[x]]与P[j-1]，如果相同则求得next[j] = next[x]+1，否则重复跳到下一个next位置匹配这一步骤，直到P[0]仍然不同于P[j-1]就可以得到next[j] = 0；
       
    3. 根据next数组跳到P[0]都不匹配，说明next[j]=0.

  • 快速求next数组的逻辑证明

    这里不再画图用反证法，尝试用文字直接证明：

    1. 设next[j] = x，根据定义P[0, x-1] == P[j-x, j-1]，即P[0, x-2] == P[j-x, j-2]，已经求得满足第二个等式的x-2最大值就是next[j-1]-1，所以当且仅当P[j-1] == P[next[j-1]]时next[j]能取到最大值next[j-1]+1。
    2. 设next[j-1] = y，如果P[j-1] != P[y]，那么求next[j]只能在[0, y-1]范围内找能满足P[0, x-1] == P[j-x, j-1]的x最大值，由于P[j-x, j-2] == P[y-x+1, y-1]，所以P[j-x, j-2] == P[y-x+1, y-1] == P[0, x-2]，根据next[y]定义可知x-2最大只能取得next[y]+1，得出结论当且仅当P[j-1] == P[next[y]]时next[j]能取到最大值next[y]+1。

• 代码示例

    public static int firstIndexOf(String str, String pattern) {
        if (str == null || pattern == null) {
            return -1;
        }
        char[] S = str.toCharArray(), P = pattern.toCharArray();
        if (pattern.length() < 3) {
            return forcibleFind(S, P);
        }
        int[] next = nextArray(P);
        int i = 0, j = 0;
        while (i < S.length) {
            if (S[i] == P[j]) {// case1: 字符匹配，两个下标同时右移+1
                i++;
                j++;
            }
            else if (j > 0) {// case2: 不匹配，主串下标不变，子串下标跳到next
                j = next[j];
            }
            else {// 子串下标已经跳到首位仍然不匹配，主串下标右移
                i++;
            }
            if (j == P.length) {
                // 子串匹配完成，返回对应的主串下标
                return i - j;
            }
        }
        return -1;
    }
  
    /**
     * 子串长度不超过2时没必要再生成next数组了，直接暴力匹配
     */
    private static int forcibleFind(char[] S, char[] P) {
        if (P.length < 1) {
            return 0;
        }
        if (P.length > 2) {
            throw new UnsupportedOperationException("只支持最长为2的子串暴力匹配");
        }
        int i = 0, j = 0;
        while (i < S.length) {
            if (S[i++] == P[j]) {
                j++;
            }
            else if (j > 0) {
                j = 0;
                i--;
            }
            if (j == P.length) {
                return i - j;
            }
        }
        return -1;
    }
  
    /**
     * 求next数组
     */
    private static int[] nextArray(char[] p) {
        if (p.length < 2) {
            return new int[]{-1};
        }
        int[] next = new int[p.length];
        next[0] = -1;
        next[1] = 0;
        int i = 2, pre = 0;
        while (i < p.length) {
            if (p[i - 1] == p[pre]) {// case1: next[i] = next[i-1] + 1
                next[i++] = ++pre;
            }
            else if (pre > 0) {// case2: next[i-1] > 0 时 继续匹配 next[next[i-1]]
                pre = next[pre];
            }
            else {// case3: pre == 0 已经跳到了首位字符仍然不匹配
                next[i++] = 0;
            }
        }
        return next;
    }
  

温习参考链接：【左神的B站视频】KMP算法原理和代码详解