Leetcode练习3之数据结构
链表
链表是空节点,或者有一个值和一个指向下一个链表的指针,因此很多链表问题可以用递归来处理。
8. 回文链表
234. Palindrome Linked List (Easy)
题目要求:以 O(1) 的空间复杂度来求解。
切成两半,把后半段反转,然后比较两半是否相等。
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ class Solution { public boolean isPalindrome(ListNode head) { if (head == null || head.next == null) { return true; } ListNode slow = head; ListNode fast = head.next; while (fast != null && fast.next != null) { slow = slow.next; fast = fast.next.next; } if (fast != null) { slow = slow.next; } cut(head, slow); return isEqual(head, reverse(slow)); } private void cut (ListNode head, ListNode cutNode) { while (head.next != cutNode) { head = head.next; } head.next = null; } private ListNode reverse (ListNode head) { ListNode newHead = null; while (head != null) { ListNode nextNode = head.next; head.next = newHead; newHead = head; head = nextNode; } return newHead; } private boolean isEqual (ListNode l1, ListNode l2) { while (l1 != null && l2 != null) { if (l1.val != l2.val) { return false; } l1 = l1.next; l2 = l2.next; } return true; } }
9. 分隔链表
725. Split Linked List in Parts(Medium)
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ class Solution { public ListNode[] splitListToParts(ListNode root, int k) { int N = 0; ListNode cur = root; while (cur != null) { N++; cur = cur.next; } int mod = N % k; int size = N / k; ListNode[] ret = new ListNode[k]; cur = root; for (int i = 0; cur != null && i < k; i++) { ret[i] = cur; int curSize = size + (mod-- > 0? 1 : 0); for (int j = 0; j < curSize - 1; j++) { cur = cur.next; } ListNode next = cur.next; cur.next = null; cur = next; } return ret; } }
树
递归
9. 树的对称
101. Symmetric Tree (Easy)
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public boolean isSymmetric(TreeNode root) { if (root == null) { return true; } return isSymmetric(root.left, root.right); } private boolean isSymmetric (TreeNode t1, TreeNode t2) { if (t1 == null && t2 == null) { return true; } if (t1 == null || t2 == null) { return false; } if (t1.val != t2.val) { return false; } return isSymmetric(t1.left, t2.right) && isSymmetric(t1.right, t2.left); } }
前中后序遍历
1
/ \
2 3
/ \ \
4 5 6
- 层次遍历顺序:[1 2 3 4 5 6]
- 前序遍历顺序:[1 2 4 5 3 6]
- 中序遍历顺序:[4 2 5 1 3 6]
- 后序遍历顺序:[4 5 2 6 3 1]
层次遍历使用 BFS 实现,利用的就是 BFS 一层一层遍历的特性;而前序、中序、后序遍历利用了 DFS 实现。
前序、中序、后序遍只是在对节点访问的顺序有一点不同,其它都相同。
① 前序
void dfs(TreeNode root) {
visit(root);
dfs(root.left);
dfs(root.right);
}
② 中序
void dfs(TreeNode root) {
dfs(root.left);
visit(root);
dfs(root.right);
}
③ 后序
void dfs(TreeNode root) {
dfs(root.left);
dfs(root.right);
visit(root);
}
1. 非递归实现二叉树的前序遍历
144. Binary Tree Preorder Traversal (Medium)
递归方式
class Solution { public List<Integer> preorderTraversal(TreeNode root) { List<Integer> resultList = new ArrayList<>(); return preorderTraversal(root, resultList); } private List<Integer> preorderTraversal(TreeNode root, List<Integer> resultList) { if (root == null) { return resultList; } resultList.add(root.val); preorderTraversal(root.left, resultList); preorderTraversal(root.right, resultList); return resultList; } }
迭代算法
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public List<Integer> preorderTraversal(TreeNode root) { List<Integer> resultList = new ArrayList<>(); Stack<TreeNode> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); if (node == null) { continue; } resultList.add(node.val); stack.push(node.right); // 先压入右节点 stack.push(node.left); } return resultList; } }
2. 非递归实现二叉树的后序遍历
145. Binary Tree Postorder Traversal (Medium)
3. 非递归实现二叉树的中序遍历
94. Binary Tree Inorder Traversal (Medium)
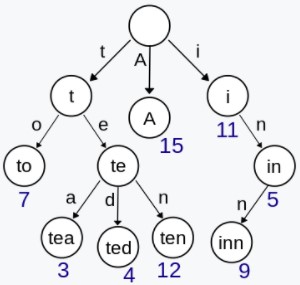
Trie
Trie,又称前缀树或字典树,用于判断字符串是否存在或者是否具有某种字符串前缀。
1. 实现一个 Trie
208. Implement Trie (Prefix Tree) (Medium)
栈和队列
计算器
哈希表
字符串
2. 字符串循环移位
数组与矩阵
矩阵最大面积
图
拓扑排序
常用于在具有先序关系的任务规划中。
1. 课程安排的合法性
207. Course Schedule (Medium)
2, [[1,0]]
return true
2, [[1,0],[0,1]]
return false
题目描述:一个课程可能会先修课程,判断给定的先修课程规定是否合法。
本题不需要使用拓扑排序,只需要检测有向图是否存在环即可。
位运算
基本原理
0s 表示一串 0,1s 表示一串 1。
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x
利用 x ^ 1s = ~x 的特点,可以将一个数的位级表示翻转;利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
1^1^2 = 2
利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。一个数 num 与 mask:00111100 进行位与操作,只保留 num 中与 mask 的 1 部分相对应的位。
01011011 &
00111100
--------
00011000
利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
01011011 |
00111100
--------
01111111
位与运算技巧
n&(n-1) 去除 n 的位级表示中最低的那一位 1。例如对于二进制表示 01011011,减去 1 得到 01011010,这两个数相与得到 01011010。
01011011 &
01011010
--------
01011010
n&(-n) 得到 n 的位级表示中最低的那一位 1。-n 得到 n 的反码加 1,也就是 -n=~n+1。例如对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
10110100 &
01001100
--------
00000100
n-(n&(-n)) 则可以去除 n 的位级表示中最低的那一位 1,和 n&(n-1) 效果一样。
移位运算
>> n 为算术右移,相当于除以 2n,例如 -7 >> 2 = -2。
11111111111111111111111111111001 >> 2
--------
11111111111111111111111111111110
>>> n 为无符号右移,左边会补上 0。例如 -7 >>> 2 = 1073741822。
11111111111111111111111111111001 >>> 2
--------
00111111111111111111111111111111
<< n 为算术左移,相当于乘以 2n。-7 << 2 = -28。
11111111111111111111111111111001 << 2
--------
11111111111111111111111111100100
mask 计算
要获取 111111111,将 0 取反即可,~0。
要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
要得到 1 到 i 位为 1 的 mask,(1<<i)-1 即可,例如将 (1<<4)-1 = 00010000-1 = 00001111。
要得到 1 到 i 位为 0 的 mask,只需将 1 到 i 位为 1 的 mask 取反,即 ~((1<<i)-1)。
Java 中的位操作
static int Integer.bitCount(); // 统计 1 的数量
static int Integer.highestOneBit(); // 获得最高位
static String toBinaryString(int i); // 转换为二进制表示的字符串
位排序