Leetcode练习之搜索

深度优先搜索和广度优先搜索广泛运用于树和图中，但是它们的应用远远不止如此。

BFS

 

广度优先搜索一层一层地进行遍历，每层遍历都是以上一层遍历的结果作为起点，遍历一个距离能访问到的所有节点。需要注意的是，遍历过的节点不能再次被遍历。

第一层：

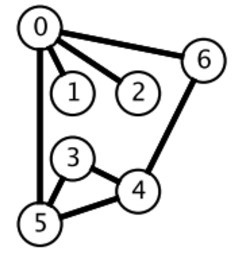
• 0 -> {6,2,1,5}

第二层：

• 6 -> {4}
• 2 -> {}
• 1 -> {}
• 5 -> {3}

第三层：

• 4 -> {}
• 3 -> {}

每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离，推导出一个结论：对于先遍历的节点 i 与后遍历的节点 j，有 di <= dj。利用这个结论，可以求解最短路径等 最优解 问题：第一次遍历到目的节点，其所经过的路径为最短路径。应该注意的是，使用 BFS 只能求解无权图的最短路径，无权图是指从一个节点到另一个节点的代价都记为 1。

在程序实现 BFS 时需要考虑以下问题：

• 队列：用来存储每一轮遍历得到的节点；
• 标记：对于遍历过的节点，应该将它标记，防止重复遍历。

1. 计算在网格中从原点到特定点的最短路径长度

1091. Shortest Path in Binary Matrix(Medium)

 

class Solution {
    public int shortestPathBinaryMatrix(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return -1;
        }
        int[][] direction = {{1,-1}, {1,0}, {1,1}, {0,-1}, {0,1}, {0,1}, {-1,-1}, {-1,0}, {-1,1}};
        int m = grid.length;
        int n = grid[0].length;
        Queue<Pair<Integer, Integer>> queue = new LinkedList<>();
        queue.add(new Pair<>(0, 0));
        int pathLength = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            pathLength++;
            while (size-- > 0){
                Pair<Integer, Integer> cur = queue.poll();
                int cr = cur.getKey();
                int cc = cur.getValue();
                if (grid[cr][cc] == 1) {
                    continue;
                }
                if (cr  == m-1 && cc == n-1) {
                    return pathLength;
                }
                grid[cr][cc] = 1;
                for (int[] d:direction) {
                    int nr = cr + d[0];
                    int nc = cc + d[1];
                    if (nr < 0 || nr >= m || nc < 0 || nc >= n) {
                        continue;
                    }
                    queue.add(new Pair<>(nr, nc));
                }
            }
        }
        return -1;
    }
}