LeetCode.62——不同路径
-
问题描述:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
![]()
例如,上图是一个7 x 3 的网格。有多少可能的路径?LeetCode原题
-
问题分析:
这是一个比较简单的动态规划问题,由于没有障碍 (不同路径2 网格中有障碍),
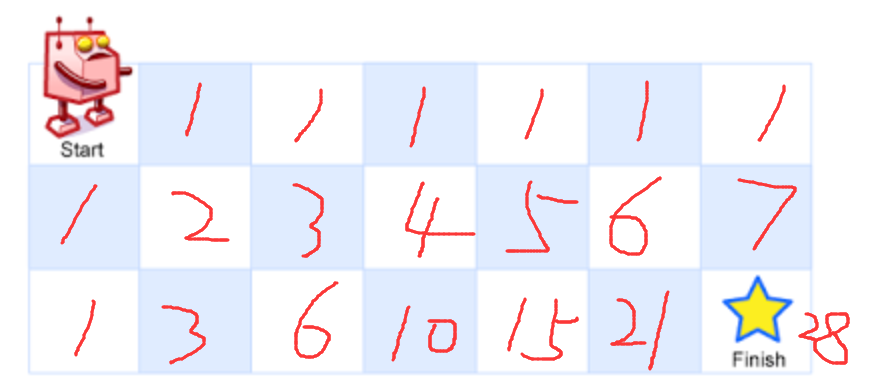
由于每一步都只能向右或者向下,那很明显,可以知道第一行和第一列的每一个格子都是1:
![]()
由于只能向右和向下,能达到2号位置的路径只有两种,右→下 或者 下→右。同理,第一行第一列以外的其他任何一个位置的路径数,都等于当前位置前面和上面的路径和。这样就可以得到最终的路径:
dp[m-1][n-1] = dp[m-1][n-2] + dp[m-2][n-1] -
代码实现:
public class UniquePaths_62{ public static void main(String[] args) { Solution4 solution = new Solution4(); int res = solution.uniquePaths(1,1); System.out.println(res); } } class Solution { public int uniquePaths(int m, int n) { //1.初始化第一行第一列 int[][] dp = new int[m][n]; for (int i = 0; i < dp.length; i++) { for (int j = 0; j < dp[0].length; j++) { dp[0][j] = 1; dp[i][0] = 1; } } for (int i = 1; i < dp.length; i++) { for (int j = 1; j < dp[0].length; j++) { dp[i][j] = dp[i][j-1] + dp[i-1][j]; } } return dp[m-1][n-1]; } }性能:
(1)时间复杂度:O(m*n)
(2)空间复杂度:O(m*n)
-
最后 :
由于个人水平有限,博文中难免有错误或表达不准确之处,欢迎各位大佬批评指正。如有更好的方法,欢迎评论区留下你的高见,欢迎转载转发,记得注明出处。码字不易,如有帮助,欢迎打赏一杯熬夜咖啡,谢谢老板~~~
![]()
人生无完美,曲折亦风景.





 浙公网安备 33010602011771号
浙公网安备 33010602011771号