0-1背包问题

---

• 问题描述：

  有 n 件物品和一个最大承重为 W 的背包，每件物品的重量是 𝑤i、价值是 𝑣i

  在保证总重量不超过 W 的前提下，选择某些物品装入背包，背包的最大总价值是多少？

  注意：每个物品只有 1 件，也就是每个物品只能选择 0 件或者 1 件

• 问题分析：

  这是一个典型的动态规划问题：

  ​ 1.设置一个values的物品价值数组和一个相对应的物品重量数组weigths.

  ​ 2.物品的编号为i，由于后续使用数组下标的原因，i从1开始，所以：价值是values[i-1],重量为weights[i-1]。

  ​ 3.状态方程：

  dp[i][j] = 表示有前i个物品可以选择，且背包容量为j的情况下可以获取的最大价值
  

  ​ 4.当 j < weights[ i -1 ]时：

  dp[i][j] = dp[i-1][j];
  

  ​ 5.当 j > = weights[i-1] 时：

  dp [i][j] = Math.max (dp[i – 1, j], dp[i – 1, j – weights[i – 1]] + values[i – 1] )
  values[i – 1] //表示当前物品的价值  
  dp[i – 1, j – weights[i – 1]] // 表示取了当前物品后剩余空间的最大价值
  //综合：当j > = weights[i-1] 时，当前的物品可以选择取或者不取
      (1)不取的话，很明显，最大价值就是上一步的最大价值dp[i][j] = dp[i-1][j]
      (2)取的话，价值就为dp[i – 1, j – weights[i – 1]] + values[i – 1]
  //由于不知道取还是不取时获得的价值最高，所以对两个数取最大值。
  

• 代码实现：

  class Solution{
      public void knapsackProblem(){
          int[] weight = {2,2,6,5,4};
          int[] values = {6,3,5,4,6};
          int capacity = 10;
          int n = values.length;
          //因为要空出第一行和第一列 所以dp数组要加一
          int[][] dp = new int[values.length+1][capacity+1];
  
          for (int i = 1; i < dp.length; i++) {
              for (int j = 1; j < dp[0].length; j++) {
                  if (j < weight[i-1]){
                      dp[i][j] = dp[i-1][j];
                  }else {
                      dp[i][j] = Math.max(dp[i-1][j],values[i-1]+dp[i-1][j-weight[i-1]]);
                  }
              }
          }
  		//输出二维数组
          for (int i = 0; i < dp.length; i++) {
              for (int j = 0; j < dp[0].length; j++) {
                  System.out.print(dp[i][j] + "  ");
              }
              System.out.println();
          }
  		//最终结果
          System.out.println(dp[values.length][capacity]);
      }
  }
  
  

• 方案优化

  

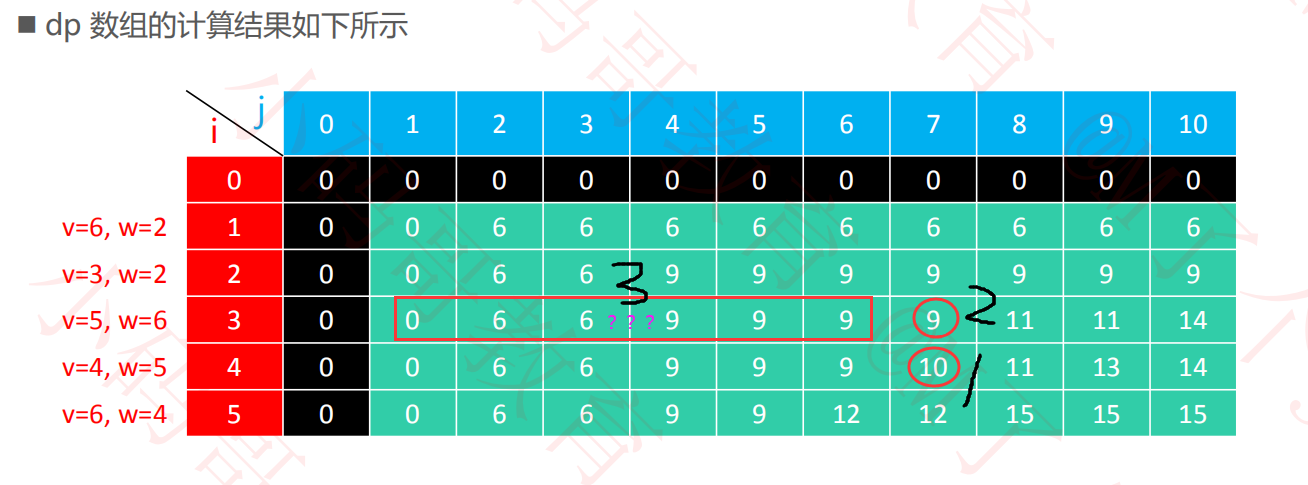
  ​ 比如当我们求dp[4][7]的时候，只有两种选择，要么去4号物品，要么不取。如果不取的话，那这一决策的最大价值就是上一步决策得到的最大价值dp[3][7],如果取的话，就是当前物品的价值加上剩余空间的最大价值dp[ 3 ][ 2 ] = 6, 6+4 = 10.和图中结果一样。

  由上一个方案的执行过程我们可以发现这样的规律：

  ​ 当我们求dp[i][j]时，只会用到其当前物品的价值和上一步决策的最大值（2号区域）以及前面的某一个数值（3号区域），那么我们就可以把它简化成一维数组，从后往前求取，这样可以使得代码更加简单。

• 优化代码实现：

  package DynamicProgramming;
  
  public class KnapsackBest {
      public static void main(String[] args){
          int[] w = {1,3,5,4,3};
          int[] v = {5,7,10,8,6};
          int c = 10;
          System.out.println(maxValue(w,v,c));
  
      }
  
      public static int maxValue(int[] w,int[] v,int c){
          //判断数组是否符合要求
          if (w.length == 0 || w == null) return 0;
          if (v.length == 0 || v == null) return 0;
          if (w.length != v.length || c <= 0) return 0;
  		//用于存储决策价值的数组
          int[] dp = new int[c+1];
          for (int i = 1; i < v.length+1 ; i++) {
              //从后往前遍历，当j < w[i-1]的情况下，直接使用上一步的数组结果
              for (int j = c; j >= w[i-1] ; j--) {
                  //从后往前，覆盖上一物品时产生的结果
                  dp[j] = Math.max(dp[j],v[i-1] + dp[j-w[i-1]]);
              }
          }
  
          return dp[c];
      }
  }
  

---

• 最后 ：

  由于个人水平有限，博文中难免有错误或表达不准确之处，欢迎各位大佬批评指正。如有更好的方法，欢迎评论区留下你的高见，欢迎转载转发，记得注明出处。码字不易，如有帮助，欢迎打赏一杯熬夜咖啡，谢谢老板~~~