leetcode:304. 二维区域和检索 - 矩阵不可变
链接:https://leetcode-cn.com/problems/range-sum-query-2d-immutable/
使用暴力解法,没想到竟然过了。
class NumMatrix {
int[][] matrix;
public NumMatrix(int[][] matrix) {
this.matrix = matrix;
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum = 0;
for (int i = row1; i <= row2; i++) {
for (int j = col1; j <= col2; j++) {
sum += matrix[i][j];
}
}
return sum;
}
}
注意题目说会多次调用sumRegion方法,所以暴力解法指不定就超时了。
这里可以使用动态规划求解。假设
f
(
i
,
j
)
表
示
矩
阵
中
以
(
i
,
j
)
为
右
下
脚
顶
点
的
左
上
方
矩
阵
的
区
域
和
f(i, j) 表示矩阵中以(i, j)为右下脚顶点的左上方矩阵的区域和
f(i,j)表示矩阵中以(i,j)为右下脚顶点的左上方矩阵的区域和
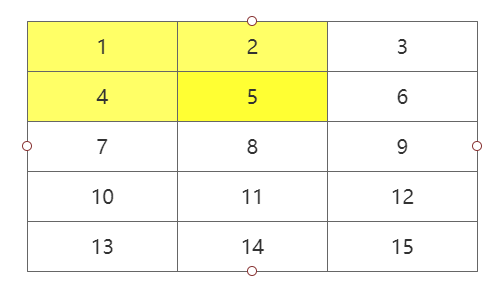
如上图,就表示f(1, 1)的值。那么可知,对于任意f(i, j),计算公式如下
f
(
i
,
j
)
=
f
(
i
,
j
−
1
)
+
f
(
i
−
1
,
j
)
−
f
(
i
−
1
,
j
−
1
)
+
m
a
t
r
i
x
[
i
]
[
j
]
f(i,j) = f(i,j-1) + f(i-1,j) - f(i-1,j-1) + matrix[i][j]
f(i,j)=f(i,j−1)+f(i−1,j)−f(i−1,j−1)+matrix[i][j]
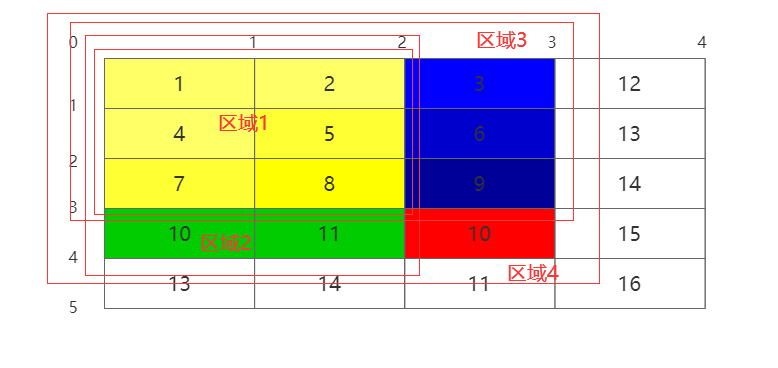
区域4:f(i, j)
区域3:f(i - 1, j)
区域2:f(i, j - 1)
区域1:f(i - 1, j - 1)
所以:区域4 = 区域3 + 区域2 - 区域1 + 10(matrix [i] [j])
有了上面的公式就好办了,对于任意的两个点(row1, col1)、(row2, col2)都可以围成一个矩形区域,假设其区域和为sum:
s
u
m
=
f
(
r
o
w
2
,
c
o
l
2
)
−
f
(
r
o
w
2
,
c
o
l
1
−
1
)
−
f
(
r
o
w
1
−
1
,
c
o
l
2
)
+
f
(
r
o
w
1
−
1
,
c
o
l
1
−
1
)
sum = f(row2, col2) - f(row2, col1 - 1) - f(row1 - 1, col2) + f(row1 - 1, col1 - 1)
sum=f(row2,col2)−f(row2,col1−1)−f(row1−1,col2)+f(row1−1,col1−1)
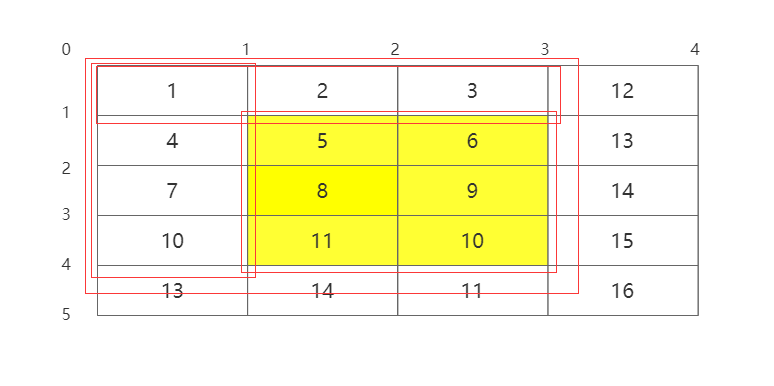
也是划分成了4个区域进行求解。代码如下
class NumMatrix {
int[][] sum;
public NumMatrix(int[][] matrix) {
// matrix可能是空数组
int m = matrix.length, n = (m == 0) ? 0 : matrix[0].length;
// 横竖长度都在matrix的基础上+1,这样循环时下标可以从1开始,避免判断i - 1,j - 1越界的情况
sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
// 因为前面横竖都+1,所以这里也要+1
row1++;
col1++;
row2++;
col2++;
return sum[row2][col2] - sum[row2][col1 - 1] - sum[row1 - 1][col2] + sum[row1 - 1][col1 - 1];
}
}
时间复杂度O(n * m),空间复杂度O(n * m)
这个击败率。。。。在sumRegion函数中其实还可以进行一些特殊情况的判断,从而提前返回。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号