AdaBoost 算法-分析波士顿房价数据集

公号：码农充电站pro
主页：https://codeshellme.github.io

在机器学习算法中，有一种算法叫做集成算法，AdaBoost 算法是集成算法的一种。我们先来看下什么是集成算法。

1，集成算法

通常，一个 Boss 在做一项决定之前，会听取多个 Leader 的意见。集成算法就是这个意思，它的基本含义就是集众算法之所长。

前面已经介绍过许多算法，每种算法都有优缺点。那么是否可以将这些算法组合起来，共同做一项决定呢？答案是肯定的。这就诞生了集成算法（Ensemble Methods）。

集成算法的基本架构如下：

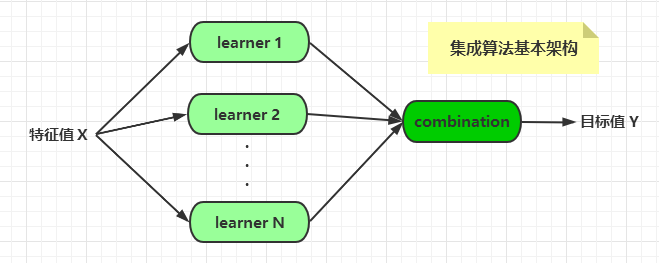
在这里插入图片描述

算法的组合有多种形式，比如将不同的算法集成起来，或者将同一种算法以不同的形式集成起来。

常见的集成算法有四大类：

  • bagging：装袋法，代表算法为 RandomForest（随机森林）。
  • boosting：提升法，代表算法有 AdaBoost，XGBoost 等。
  • stacking：堆叠法。
  • blending：混合法。

多个算法以不同的方式可以组合成集成算法，如果再深入探究的话，不同的集成方法也可以组合起来：

  • 如果将 boosting 算法的输出作为bagging 算法的基学习器，得到的是 MultiBoosting 算法；
  • 如果将 bagging 算法的输出作为boosting 算法的基学习器，得到的是 IterativBagging 算法。

对于集成算法的集成，这里不再过多介绍。

2，bagging 与 boosting 算法

bagging和 boosting是两个比较著名的集成算法。

bagging 算法

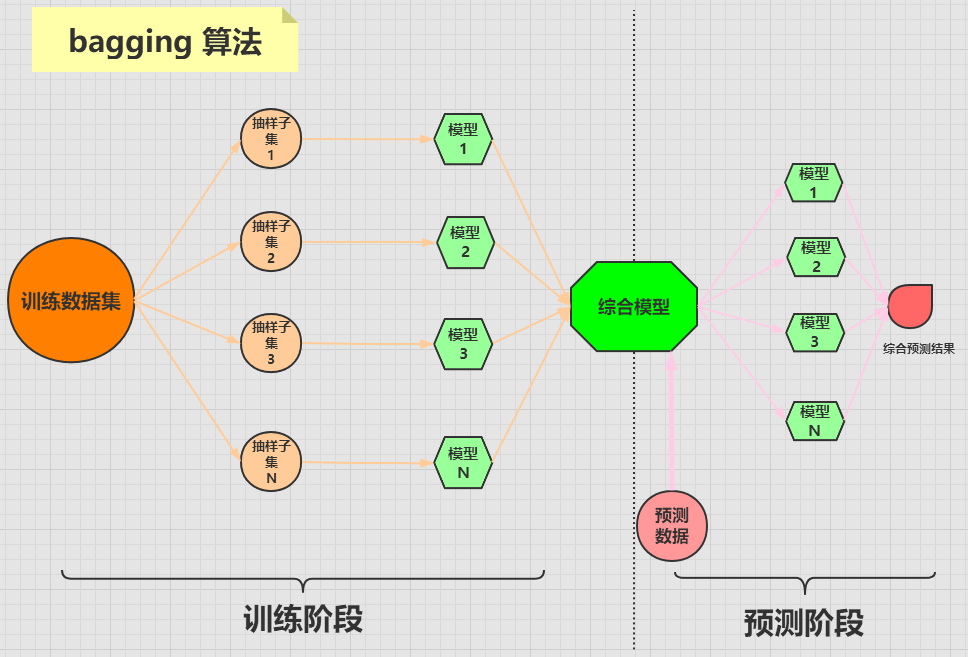
bagging 算法是将一个原始数据集随机抽样成 N 个新的数据集。然后将这N 个新的数据集作用于同一个机器学习算法，从而得到 N 个模型，最终集成一个综合模型。

在对新的数据进行预测时，需要经过这 N 个模型（每个模型互不依赖干扰）的预测（投票），最终综合 N 个投票结果，来形成最后的预测结果。

在这里插入图片描述

boosting 算法

boosting 算法的含义为提升学习，它将多个弱分类器组合起来形成一个强分类器。

boosting 算法是将一个原始数据集使用同一个算法迭代学习 N 次，每次迭代会给数据集中的样本分配不同的权重。

分类正确的样本会在下一次迭代中降低权重，而分类错误的样本会在下一次迭代中提高权重，这样做的目的是，使得算法能够对其不擅长（分类错误）的数据不断的加强提升学习，最终使得算法的成功率越来越高。

每次迭代都会训练出一个新的带有权重的模型，迭代到一定的次数或者最终模型的错误率足够低时，迭代停止。最终集成一个强大的综合模型。

在对新的数据进行预测时，需要经过这 N 个模型的预测，每个模型的预测结果会带有一个权重值，最终综合 N 个模型结果，来形成最后的预测结果。

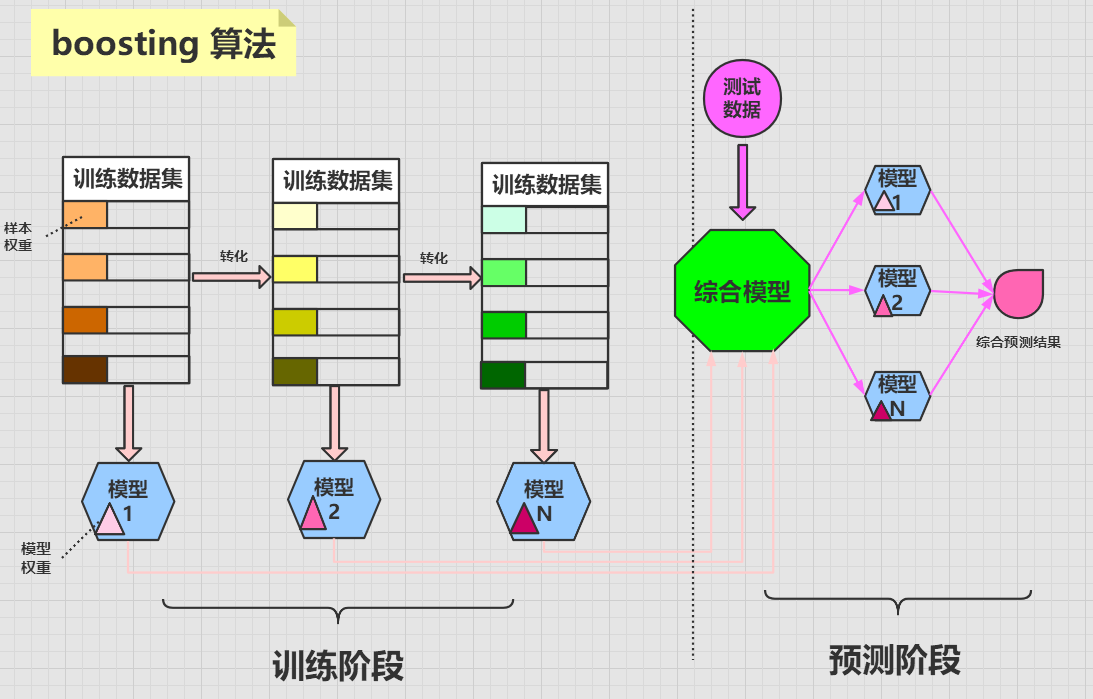
在这里插入图片描述

boosting 算法中每个模型的权重是不相等的，而bagging 算法中每个模型的权重是相等的。

3，AdaBoost 算法

AdaBoost 算法是非常流行的一种 boosting 算法，它的全称为 Adaptive Boosting，即自适应提升学习。

AdaBoost 算法由Freund 和 Schapire 于1995 年提出。这两位作者写了一篇关于AdaBoost 的简介论文，这应该是关于AdaBoost 算法的最权威的资料了。为了防止链接丢失，我将论文下载了，放在了这里。

AdaBoost 算法 和 SVM 算法被很多人认为是监督学习中最强大的两种算法。

AdaBoost 算法的运行过程如下：

  1. 为训练集中的每个样本初始化一个权重 wi，初始时的权重都相等。
  2. 根据样本训练出一个模型 Gi，并计算该模型的错误率 ei 和权重 ai。
  3. 根据权重 ai 将每个样本的权重调整为 wi+1，使得被正确分类的样本权重降低，被错误分类的样本权重增加（这样可以着重训练错误样本）。
  4. 这样迭代第2，3 步，直到训练出最终模型。

这个过程中，我们假设 x 为样本，Gi(x) 为第 i 轮训练出的模型，ai 为 Gi(x) 的权重，一共迭代 n 轮，那么最终模型 G(x) 的计算公式为：

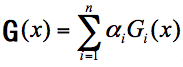
在这里插入图片描述

模型权重 ai 的计算公式如下，其中 ei 为第 i 轮模型的错误率：

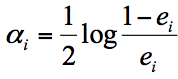
在这里插入图片描述

我们用 Dk+1 ​代表第 k+1 轮的样本的权重集合，用 Wk+1,1 代表第 k+1 轮中第1个样本的权重， Wk+1,N 代表第 k+1 轮中第 N 个样本的权重，用公式表示为：

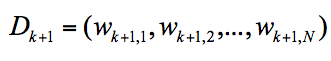
在这里插入图片描述

样本权重 Wk+1,i 的计算公式为：

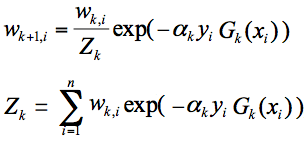
在这里插入图片描述

其中：

  • yi 为 xi 的目标值。
  • Zk 为归一化因子，使得 Dk+1 成为一个概率分布。
  • exp 为指数函数。

4，AdaBoost 算法示例

下面我们以一个二分类问题，来看一下AdaBoost 算法的计算过程。

假设我们有10 个样本数据，X 为特征集，Y 为目标集，如下：

X Y
0 1
1 1
2 1
3 -1
4 -1
5 -1
6 1
7 1
8 1
9 -1

假设有三个分类器，分别以2.5，5.5，8.5将数据分界：

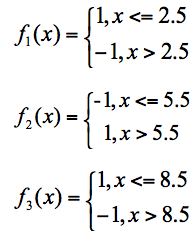
在这里插入图片描述

简单看下其分布图：

根据这三个分类器，我们可以算出每个样本对应的值：

X Y f1(x) f2(x) f3(x)
0 1 1 -1 1
1 1 1 -1 1
2 1 1 -1 1
3 -1 -1 -1 1
4 -1 -1 -1 1
5 -1 -1 -1 1
6 1 -1 1 1
7 1 -1 1 1
8 1 -1 1 1
9 -1 -1 1 -1

上面表格中，对于每个分类器分类错误的数据，我进行了标红。

第一轮

将每个样本的权重初始化为0.1：

  • D1 = (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1)

根据 D1 计算每个分类器的错误率：

  • e1(x) = 0.1*3 = 0.3
  • e2(x) = 0.1*4 = 0.4
  • e3(x) = 0.1*3 = 0.3

选择错误率最小的分类器作为第1轮的分类器，因为 f1(x)和 f3(x) 的错误率都是0.3，所以可以任意选一个，比如我们选 f1(x)，所以 G1(x) = f1(x)。

计算 G1(x) 的权重 a1(x)：

  • a1(x) = (1/2) * log((1-0.3)/0.3) = 0.42

这里的 log 以 e 为底。

计算第2轮的样本权重D2，首先需要根据Zk 的公式来计算 Z1，先计算 -a1yiG1(xi) ，如下：

序号 i yi G1(xi) -a1yiG1(xi)
1 1 1 -0.42 x 1 x 1 => -0.42
2 1 1 -0.42 x 1 x 1 => -0.42
3 1 1 -0.42 x 1 x 1 => -0.42
4 -1 -1 -0.42 x -1 x -1 => -0.42
5 -1 -1 -0.42 x -1 x -1 => -0.42
6 -1 -1 -0.42 x -1 x -1 => -0.42
7 1 -1 -0.42 x 1 x -1 => 0.42
8 1 -1 -0.42 x 1 x -1 => 0.42
9 1 -1 -0.42 x 1 x -1 => 0.42
10 -1 -1 -0.42 x -1 x -1 => -0.42

那么 Z1 = 0.1 * (7 * e^-0.42 + 3 * e^0.42) = 0.92

再根据样本权重的计算公式可以得出：

  • D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)

第二轮

根据 D2 计算每个分类器的错误率：

  • e1(x) = 0.1666*3 = 0.4998
  • e2(x) = 0.0715*4 = 0.286
  • e3(x) = 0.0715*3 = 0.2145

选择错误率最小的分类器作为第2轮的分类器，所以 G2(x) = f3(x)。

计算 G2(x) 的权重 a2(x)：

  • a2(x) = (1/2) * log((1-0.2145)/0.2145) = 0.65

计算第3轮每个样本的权重：

  • D3 = (0.0455,0.0455,0.0455,0.1667, 0.1667,0.01667,0.1060, 0.1060, 0.1060, 0.0455)

这里省略了D3 的计算过程，其计算过程与D2 一样。

第三轮

根据 D3 计算每个分类器的错误率：

  • e1(x) = 0.1060*3 = 0.318
  • e2(x) = 0.0455*4 = 0.182
  • e3(x) = 0.1667*3 = 0.5

选择错误率最小的分类器作为第3轮的分类器，所以 G3(x) = f2(x)。

计算 G3(x) 的权重 a3(x)：

  • a3(x) = (1/2) * log((1-0.182)/0.182) = 0.75

如果我们只迭代三轮，那么最终的模型 G(x) = 0.42G1(x) + 0.65G2(x) + 0.75G3(x)。

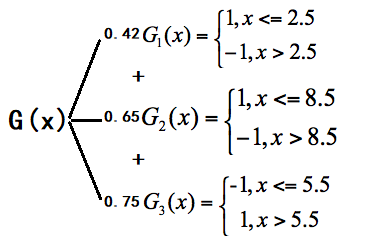
在这里插入图片描述

有了最终的模型G(x)，我们根据G(x) 来计算每个样本对应的值：

G0 = 0.42 + 0.65 - 0.75  = 0.32  =>  1
G1 = 0.42 + 0.65 - 0.75  = 0.32  =>  1
G2 = 0.42 + 0.65 - 0.75  = 0.32  =>  1
G3 = -0.42 + 0.65 - 0.75 = -0.52 => -1
G4 = -0.42 + 0.65 - 0.75 = -0.52 => -1
G5 = -0.42 + 0.65 - 0.75 = -0.52 => -1
G6 = -0.42 + 0.65 + 0.75 = 0.98  =>  1
G7 = -0.42 + 0.65 + 0.75 = 0.98  =>  1
G8 = -0.42 + 0.65 + 0.75 = 0.98  =>  1
G9 = -0.42 - 0.65 + 0.75 = -0.32 => -1

因为本例是一个二分类问题，所以对于值大于 0 均取 1，值小于 0 均取 -1。

最终可以得到如下表格：

X Y G(x)
0 1 1
1 1 1
2 1 1
3 -1 -1
4 -1 -1
5 -1 -1
6 1 1
7 1 1
8 1 1
9 -1 -1

可以看到经过提升学习后的模型的准确率提高到了100%。

当然对于实际问题，准确率基本达不到100%。

以上就是一个简化版的 AdaBoost 算法的计算过程。

本例的原型出自《统计学习方法 · 李航》

5，sklearn 对 AdaBoost 的实现

sklearn 库的 ensemble 模块实现了一系列的集成算法，对于集成方法的介绍，可以参看这里。

AdaBoost 算法即可用于分类问题，也可用于回归问题：

来看下 AdaBoostClassifier 类的原型：

AdaBoostClassifier(
  base_estimator=None, 
  n_estimators=50, 
  learning_rate=1.0, 
  algorithm='SAMME.R', 
  random_state=None)

其参数含义：

  • base_estimator：代表弱分类器，默认使用的是决策树。
    • 对于 AdaBoostClassifier 默认使用的是 DecisionTreeClassifier(max_depth=1)。
    • 对于 AdaBoostRegressor 默认使用的是 DecisionTreeRegressor(max_depth=3)。
    • 一般不需要修改这个参数，当然也可以指定具体的分类器。
  • n_estimators：最大迭代次数，也是分类器的个数，默认是 50。
  • learning_rate：代表学习率，取值在 0-1 之间，默认是 1.0。
    • 学习率和迭代次数是相关的，如果学习率较小，就需要比较多的迭代次数才能收敛。
    • 所以如果调整了 learning_rate，一般也需要调整 n_estimators 。
  • algorithm：代表采用哪种 boosting 算法，有两种选择：SAMME 和 SAMME.R，默认是 SAMME.R。
    • SAMME 和 SAMME.R 的区别在于对弱分类权重的计算方式不同。
    • SAMME.R 的收敛速度通常比 SAMME 快。
  • random_state：代表随机数种子，默认是 None。
    • 随机种子用来控制随机模式，当随机种子取了一个值，也就确定了一种随机规则，其他人取这个值可以得到同样的结果。
    • 如果不设置随机种子，每次得到的随机数也就不同。

再来看下 AdaBoostRegressor 类的原型：

AdaBoostRegressor(
  base_estimator=None, 
  n_estimators=50, 
  learning_rate=1.0, 
  loss='linear', 
  random_state=None)

可以看到，回归和分类的参数基本一致，而回归算法里没有 algorithm 参数，但多了 loss 参数。

loss 参数代表损失函数，用于（每次迭代后）更新样本的权重，其共有 3 种选择，分别为：

  • linear，代表线性函数。
  • square，代表平方函数。
  • exponential，代表指数函数。
  • 默认是 linear，一般采用线性就可得到不错的效果。

6，使用 AdaBoost 进行回归分析

接下来，我们看下如何用 AdaBoost 算法进行回归分析。

之前在文章《决策树算法-实战篇-鸢尾花及波士顿房价预测》中，我们介绍过波士顿房价数据集，这里不再对数据本身进行过多介绍，下面我们用 AdaBoost 算法来分析该数据集。

首先加载数据集：

from sklearn.datasets import load_boston

boston = load_boston()
features = boston.data # 特征集
prices = boston.target # 目标集

将数据拆分成训练集和测试集：

from sklearn.model_selection import train_test_split
train_x, test_x, train_y, test_y = train_test_split(
    features, prices, test_size=0.25, random_state=33)

构建 AdaBoost 回归模型：

from sklearn.ensemble import AdaBoostRegressor
regressor = AdaBoostRegressor()  # 均采用默认参数
regressor.fit(train_x, train_y)  # 拟合模型

使用模型进行预测：

pred_y = regressor.predict(test_x)

评价模型准确率：

from sklearn.metrics import mean_squared_error

mse = mean_squared_error(test_y, pred_y)
print "AdaBoost 均方误差 = ", round(mse, 2) # 18.57

7，分析 AdaBoost 模型的属性

base_estimator_ 属性是基学习器，也就是训练之前的模型：

>>> regressor.base_estimator_
DecisionTreeRegressor(criterion='mse', 
    max_depth=3, max_features=None,
    max_leaf_nodes=None, min_impurity_decrease=0.0,
    min_impurity_split=None, min_samples_leaf=1,
    min_samples_split=2, min_weight_fraction_leaf=0.0,
    presort=False, random_state=None, splitter='best')

estimators_ 属性是经过训练之后的所有弱学习器，有 50 个：

>>> len(regressor.estimators_)
50

feature_importances_ 属性中存储了每个特征的重要性：

>>> regressor.feature_importances_
array([0.02104728, 0.        , 0.00304314,
       0.        , 0.00891602, 0.2825294 ,
       0.00438134, 0.17308669, 0.00929782,
       0.07457966, 0.02250937, 0.00592025, 
       0.39468902])

estimator_weights_ 属性是每个弱学习器的权重：

>>> regressor.estimator_weights_
array([2.39259487, 2.02119506, 1.68364189, 0.71892012, 2.01966649,
       1.03178435, 1.14573926, 2.15335207, 1.62996738, 1.39576421,
       1.42582945, 0.55214963, 1.17953337, 0.20934333, 0.3022646 ,
       1.73484417, 1.36590071, 0.27471584, 0.97297267, 0.21729445,
       1.97061649, 0.91072652, 1.95231025, 0.11764431, 1.19301792,
       0.21629414, 1.57477075, 1.23626619, 1.21423494, 0.24063141,
       0.08265621, 0.17198137, 0.58300858, 0.72722721, 2.07974547,
       0.61855751, 1.98179632, 0.5886063 , 0.18646107, 0.38176832,
       1.11993353, 1.81984396, 1.06785584, 0.45475221, 1.85522596,
       0.29177236, 1.0699074 , 1.79358974, 1.37771849, 0.15698322])

estimator_errors_ 属性是每个弱学习器的错误率：

>>> regressor.estimator_errors_
array([0.08373912, 0.11699548, 0.15661382, 0.32763082, 0.11715348,
       0.26273832, 0.24126819, 0.1040184 , 0.16383483, 0.19848913,
       0.19374934, 0.36536582, 0.23513611, 0.44785447, 0.42500398,
       0.149969  , 0.20328296, 0.43174973, 0.27428838, 0.44588913,
       0.12232269, 0.28685119, 0.12430167, 0.4706228 , 0.23271962,
       0.44613629, 0.17153735, 0.22508658, 0.22895259, 0.44013076,
       0.47934771, 0.45711032, 0.35824061, 0.32580349, 0.1110811 ,
       0.3501096 , 0.12112748, 0.3569547 , 0.45351932, 0.40570047,
       0.24602361, 0.1394526 , 0.25581106, 0.38823148, 0.13526048,
       0.42757002, 0.25542069, 0.14263317, 0.20137567, 0.46083459])

我们将每个弱学习器的权重和错误率使用 Matplotlib 画出折线图如下：

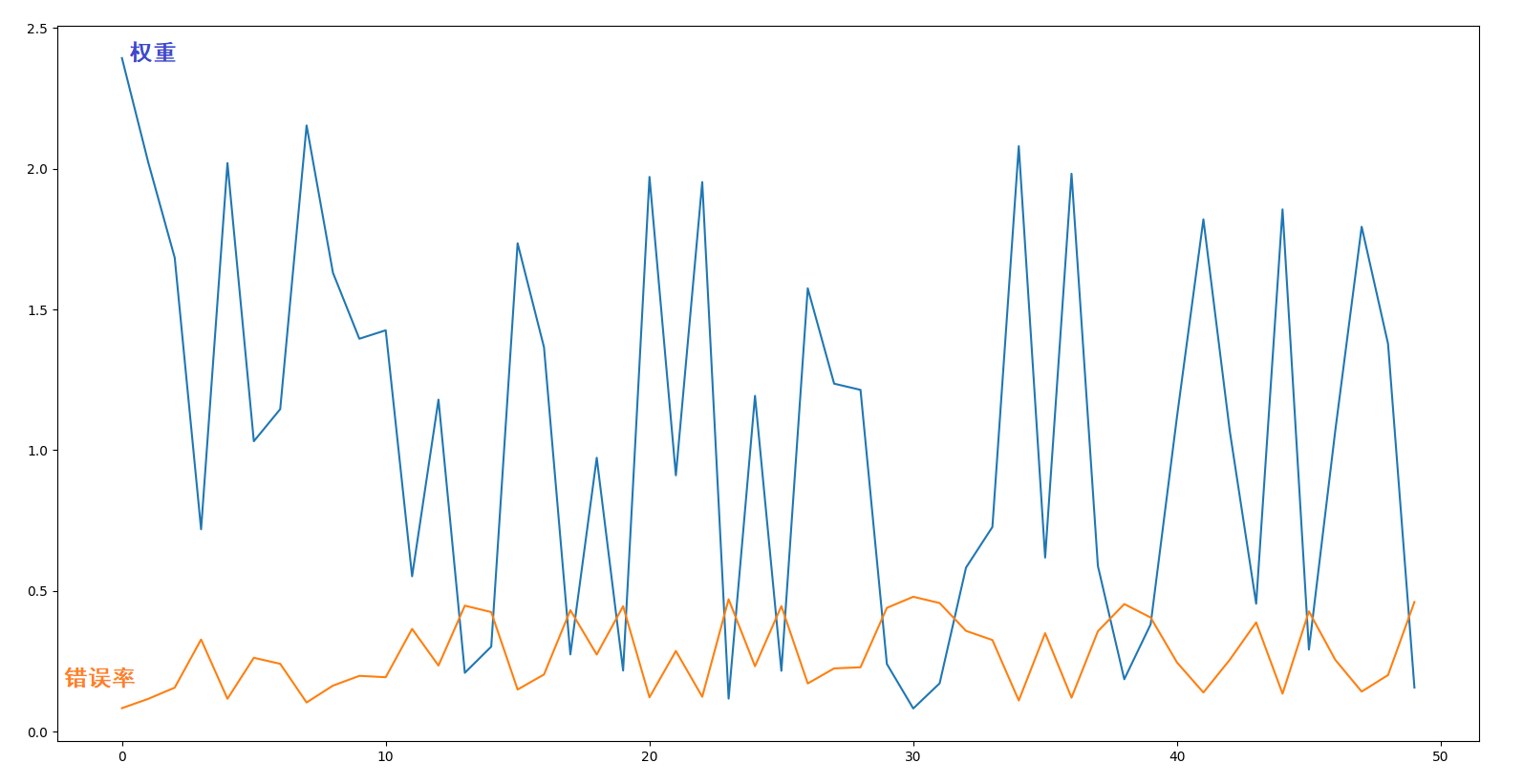
在这里插入图片描述

可以看到弱学习器的错误率与权重成反比：

  • 弱学习器的错误率越低，权重越高。
  • 弱学习器的错误率越高，权重越低。

8，对比 AdaBoost 模型与决策树，KNN 算法

下面分别使用决策树回归和KNN 回归来分析波士顿数据集，从而对比这三种算法的准确度。

使用决策树回归

代码如下

from sklearn.tree import DecisionTreeRegressor

# 构建决策树
dec_regressor = DecisionTreeRegressor()

# 拟合决策树
dec_regressor.fit(train_x, train_y)

# 预测数据
pred_y = dec_regressor.predict(test_x)

# 计算模型准确度
mse = mean_squared_error(test_y, pred_y)
print "决策树均方误差 = ", round(mse, 2)

使用KNN 回归

代码如下

from sklearn.neighbors import KNeighborsRegressor

# 构建 KNN 模型
knn_regressor = KNeighborsRegressor()

# 拟合模型
knn_regressor.fit(train_x, train_y)

# 预测数据
pred_y = knn_regressor.predict(test_x)

# 计算模型准确度
mse = mean_squared_error(test_y, pred_y)
print "KNN 均方误差 = ", round(mse, 2)

运行代码得出的结果是：

  • AdaBoost 均方误差 = 18.57
  • 决策树均方误差 = 36.92
  • KNN 均方误差 = 27.87

我们知道均方误差越小，准确率越高，所以 AdaBoost 算法在这三种算法中表现最好。

9，探究迭代次数与错误率的关系

理想情况下，迭代次数越多，最终模型的错误率应该越低，下面我们来探究一下是否是这样？

sklearn 中的 make_hastie_10_2 函数用于生成二分类数据。

我们用该函数生成12000 个数据，取前2000 个作为测试集，其余为训练集：

from sklearn import datasets

X, Y = datasets.make_hastie_10_2(n_samples=12000, random_state=1)
train_x, train_y = X[2000:], Y[2000:]
test_x, test_y = X[:2000], Y[:2000]

构建 AdaBoost 分类模型，迭代次数为 500：

from sklearn.ensemble import AdaBoostClassifier

IterationN = 500 
ada = AdaBoostClassifier(n_estimators=IterationN)
ada.fit(train_x, train_y)

对测试数据进行预测，并统计错误率：

from sklearn.metrics import zero_one_loss

errs = []
for pred_y in ada.staged_predict(test_x):
    err = zero_one_loss(pred_y, test_y)
    errs.append(err)

staged_predict 方法用于预测每一轮迭代后输入样本的预测值，所以模型迭代了多少次，该方法就会返回多少次预测结果，其返回的就是分别迭代1，2，3...N 次的预测结果。

zero_one_loss 方法用于计算错误率。

errs 列表中存储了每次迭代的错误率。

用 Matplotlib 画出错误率折线图：

import matplotlib.pyplot as plt

plt.plot(range(1, IterationN+1), errs, label='AdaBoost Error Rate', color='orange')
plt.legend(loc='upper right', fancybox=True) # 显示图例
plt.show()

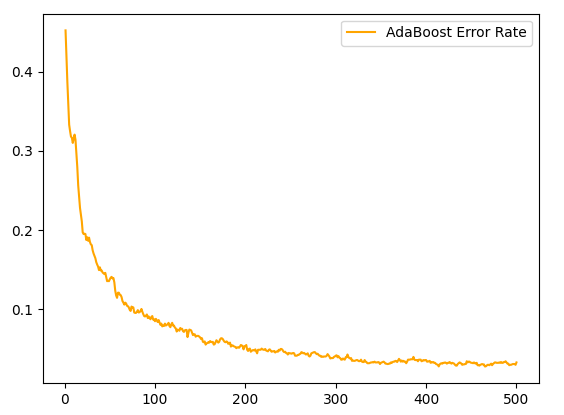
在这里插入图片描述

通过上图可以看出：

  • 随着迭代次数的增多，错误率逐渐降低。
  • 在迭代100 次之后，错误率趋于平缓。

建议：
在实际应用中，可以通过画这种折线图的方式，来判断模型应该迭代多少次。当然也要考虑时间成本，迭代次数越多，时间成本也会越高。

sklearn 官方文档中也有一个这样的例子，你可以参考这里。

需要注意的是，如果数据集不够好的话，错误率在达到一定值后有可能会反弹，即迭代次数如果再增加，错误率可能会增高，这时候就是过拟合现象。

10，总结

本篇文章主要介绍了以下内容：

  • 什么是集成算法及常见的集成算法有哪些？
  • bagging 算法与boosting 算法的区别。
  • AdaBoost 算法原理及其计算过程。
  • 使用AdaBoost 算法分析波士顿房价数据集。
  • 对比AdaBoost 算法，决策树算法及KNN 算法哪个更强大。
  • 探究AdaBoost 算法迭代次数与错误率的关系。

（本节完。）

推荐阅读：

如何使用Python 进行数据可视化

如何用Python 制作词云-对1000首古诗做词云分析

决策树算法-实战篇-鸢尾花及波士顿房价预测

Apriori 算法-如何进行关联规则挖掘

EM 算法-对鸢尾花数据进行聚类

欢迎关注作者公众号，获取更多技术干货。

码农充电站pro

posted @ 2020-12-17 15:30  码农充电站  阅读(1290)  评论(0)  编辑  收藏  举报