K 均值算法-如何让数据自动分组
公号:码农充电站pro
主页:https://codeshellme.github.io
之前介绍到的一些机器学习算法都是监督学习算法。所谓监督学习,就是既有特征数据,又有目标数据。
而本篇文章要介绍的K 均值算法是一种无监督学习。
与分类算法相比,无监督学习算法又叫聚类算法,就是只有特征数据,没有目标数据,让算法自动从数据中“学习知识”,将不同类别的数据聚集到相应的类别中。
1,K 均值算法
K 均值的英文为K-Means,其含义是:
- K:表示该算法可以将数据划分到K 个不同的组中。
- 均值:表示每个组的中心点是组内所有值的平均值。
K 均值算法可以将一个没有被分类的数据集,划分到K 个类中。某个数据应该被划分到哪个类,是通过该数据与群组中心点的相似度决定的,也就是该数据与哪个类的中心点最相似,则该数据就应该被划分到哪个类中。
关于如何计算事物之间的相似度,可以参考文章《计算机如何理解事物的相关性》。
使用K 均值算法的一般步骤是:
- 确定K 值是多少:
- 对于K 值的选择,可以通过分析数据,估算数据应该分为几个类。
- 如果无法估计确切值,可以多试几个K 值,最终将划分效果最好的K 值作为最终选择。
- 选择K 个中心点:一般最开始的K 个中心点是随机选择的。
- 将数据集中的所有数据,通过与中心点的相似度划分到不同的类别中。
- 根据类别中的数据平均值,重新计算每个类别中心点的位置。
- 循环迭代第3,4步,直到中心点的位置几乎不再改变,分类过程就算完毕。
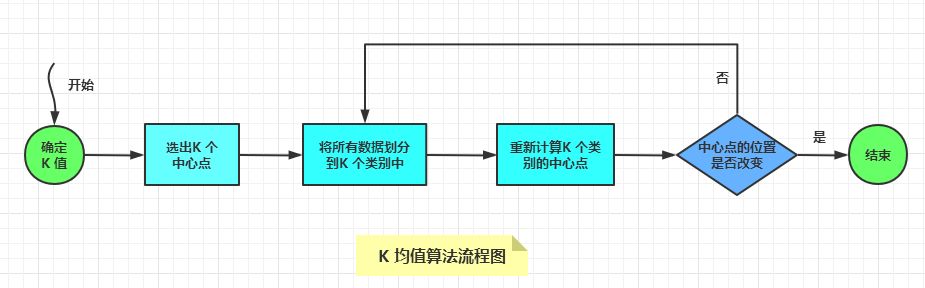
2,K 均值算法聚类过程
下面以一个二维数据点的聚类过程,来看下K 均值算法如何聚类。
首先,这里有一些离散的数据点,如下图:
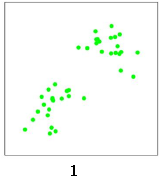
我们使用K 均值算法对这些数据点进行聚类。随机选择两个点作为两个类的中心点,分别是红色x 和蓝色x:
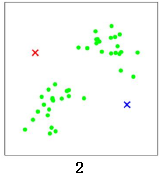
计算所有数据点到这两个中心点的距离,距离红色x 近的点标红色,距离蓝色x 近的点标蓝色:
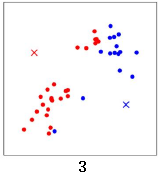
重新计算两个中心点的位置,两个中心点分别移动到新的位置:
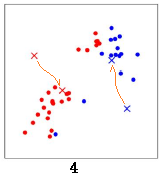
重新计算所有数据点分别到红色x 和蓝色x的距离,距离红色x 近的点标红色,距离蓝色x 近的点标蓝色:
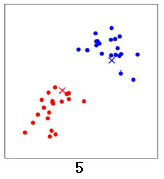
再次计算两个中心点的位置,两个中心点分别移动到新的位置:
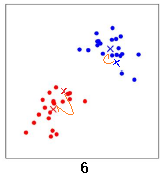
直到中心点的位置几乎不再变化,聚类结束。
以上过程就是K 均值算法的聚类过程。
3,K 均值算法的实现
K 均值算法是一个聚类算法,sklearn 库中的 cluster 模块实现了一系列的聚类算法,其中就包括K 均值算法。
来看下KMeans 类的原型:
KMeans(
n_clusters=8,
init='k-means++',
n_init=10,
max_iter=300,
tol=0.0001,
precompute_distances='deprecated',
verbose=0,
random_state=None,
copy_x=True,
n_jobs='deprecated',
algorithm='auto')
可以看KMeans 类有很多参数,这里介绍几个比较重要的参数:
- n_clusters: 即 K 值,可以随机设置一些 K 值,选择聚类效果最好的作为最终的 K 值。
- init:选择初始中心点的方式:
- init='k-means++':可加快收敛速度,是默认方式,也是比较好的方式。
- init='random ':随机选择中心点。
- 也可以自定义方式,这里不多介绍。
- n_init:初始化中心点的运算次数,默认是 10。如果 K 值比较大,可以适当增大 n_init 的值。
- algorithm:k-means 的实现算法,有auto,full,elkan三种。
- 默认是auto,根据数据的特点自动选择用full或者elkan。
- max_iter:算法的最大迭代次数,默认是300。
- 如果聚类很难收敛,设置最大迭代次数可以让算法尽快结束。
下面对一些二维坐标中的点进行聚类,看下如何使用K 均值算法。
4,准备数据点
下面是随机生成的三类坐标点,每类有20 个点,不同类的点的坐标在不同的范围内:
- A 类点:Ax 表示A 类点的横坐标,Ay 表示A 类点的纵坐标。横纵坐标范围都是 (0, 20]。
- B 类点:Bx 表示B 类点的横坐标,By 表示B 类点的纵坐标。横纵坐标范围都是 (40, 60]。
- C 类点:Cx 表示C 类点的横坐标,Cy 表示C 类点的纵坐标。横纵坐标范围都是 (70, 90]。
Ax = [20, 6, 14, 13, 8, 19, 20, 14, 2, 11, 2, 15, 19, 4, 4, 11, 13, 4, 15, 11]
Ay = [14, 19, 17, 16, 3, 7, 9, 18, 20, 3, 4, 12, 9, 17, 14, 1, 18, 17, 3, 5]
Bx = [53, 50, 46, 52, 57, 42, 47, 55, 56, 57, 56, 50, 46, 46, 44, 44, 58, 54, 47, 57]
By = [60, 57, 57, 53, 54, 45, 54, 57, 49, 53, 42, 59, 54, 53, 50, 50, 58, 58, 58, 51]
Cx = [77, 75, 71, 87, 74, 70, 74, 85, 71, 75, 72, 82, 81, 70, 72, 71, 88, 71, 72, 80]
Cy = [85, 77, 82, 87, 71, 71, 77, 88, 81, 73, 80, 72, 90, 77, 89, 88, 83, 77, 90, 72]
我们可以用 Matplotlib 将这些点画在二维坐标中,代码如下:
import matplotlib.pyplot as plt
plt.scatter(Ax + Bx + Cx, Ay + By + Cy, marker='o')
plt.show()
画出来的图如下,可看到这三类点的分布范围还是一目了然的。
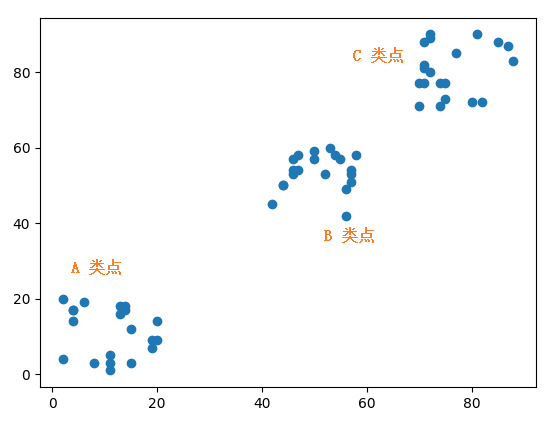
关于如何使用 Matplotlib 绘图,可以参考文章《如何使用Python 进行数据可视化》。
5,对数据聚类
下面使用K 均值算法对数据点进行聚类。
创建K 均值模型对象:
from sklearn.cluster import KMeans
# 设置 K 值为 3,其它参数使用默认值
kmeans = KMeans(n_clusters=3)
准备数据,共三大类,60 个坐标点:
train_data = [
# 前20 个为 A 类点
[20, 14], [6, 19], [14, 17], [13, 16], [8, 3], [19, 7], [20, 9],
[14, 18], [2, 20], [11, 3], [2, 4], [15, 12], [19, 9], [4, 17],
[4, 14], [11, 1], [13, 18], [4, 17], [15, 3], [11, 5],
# 中间20 个为B 类点
[53, 60], [50, 57], [46, 57], [52, 53], [57, 54], [42, 45], [47, 54],
[55, 57], [56, 49], [57, 53], [56, 42], [50, 59], [46, 54], [46, 53],
[44, 50], [44, 50], [58, 58], [54, 58], [47, 58], [57, 51],
# 最后20 个为C 类点
[77, 85], [75, 77], [71, 82], [87, 87], [74, 71], [70, 71], [74, 77],
[85, 88], [71, 81], [75, 73], [72, 80], [82, 72], [81, 90], [70, 77],
[72, 89], [71, 88], [88, 83], [71, 77], [72, 90], [80, 72],
]
拟合模型:
kmeans.fit(train_data)
对数据进行聚类:
predict_data = kmeans.predict(train_data)
查看聚类结果,其中的0,1,2 分别代表不同的类别:
>>> print(predict_data)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
通过观察最终的聚类结果predict_data,可以看到,前,中,后20 个数据分别被分到了不同的类中,也非常符合我们的预期,说明K 均值算法的聚类结果还是很不错的 。
因为本例中的二维坐标点的分布界限非常明显,所以最终的聚类结果非常不错。
我们可以通过 n_iter_ 属性来查看迭代的次数:
>>> kmeans.n_iter_
2
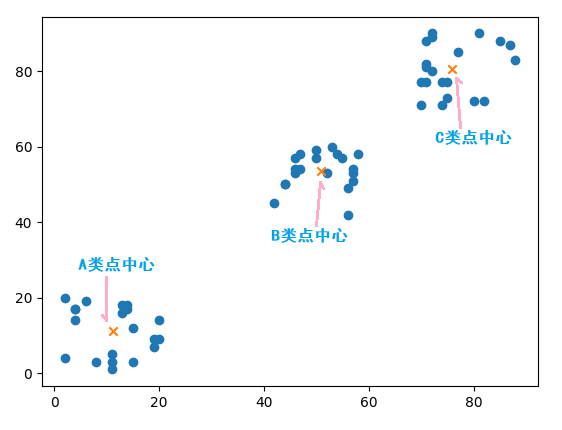
通过 cluster_centers_ 属性查看每个类的中心点坐标:
>>> kmeans.cluster_centers_
array([[11.25, 11.3 ],
[75.9 , 80.5 ],
[50.85, 53.6 ]])
将这三个中心点画在坐标轴中,如下:
6,总结
本篇文章主要介绍了K 均值算法的原理,及sklearn 库对它的实现,并且演示了如何使用K 均值算法对二维数据点进行聚类。
(本节完。)
推荐阅读:
欢迎关注作者公众号,获取更多技术干货。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号