浙江理工大学2022新生赛

浙江理工大学2022新生赛部分题目的理解

这里仅提供代码及思路，网站链接如下：
链接>http://47.96.116.66/contest.php?cid=4959<
难度梯度：J C F G B K E A H D I ——/) /)
有错误的话请联系我，我也想知道　ฅ(• - •)ฅ

A

（可能不会更了）

B

玩过飞行棋吗？这个是不是和快进机场（中间）的时候一摸一样。
我们反着思考，假设现在在终点，那么我们要一次骰子，落到k个地方的概率是相同的。
1.那么在离终点距离小于等于k时，某一个点到终点的距离的概率全是k，即dp[1]=dp[2]=······=dp[k]=k;
理解1：假设你有一个6面骰子，你走到的概率首先是\(\frac{1}{6}\),之后加上\(\frac{5}{6}*(·· ·)\)，也许可能是\(\frac{1}{6}\)，那么大约6次中能到达一次，故期望为6即k。
换一个理解：1-k的距离，需要平移k步才能让所有点有概率到达0点，那么期望为k。
2.在离终点距离大于等于k时，dp[i]=\(\frac{dp[i-1]+dp[i-2]+···+dp[i-k]}{k}+1\)
理解2：首先，该点肯定在离终点k的外面，那么它本身就不可能从重点返回来，不用考虑终点回来的情况。
那么就变成了等概率的后面k个点到第i点，步数+1
实验室的官方题解：

点击查看代码

#include <bits/stdc++.h>
#define ll long long
#define ld long double
#define Ma 1000005
using namespace std;
ll n,k;
ld dp[Ma],sum[Ma];
int main()
{
	scanf("%lld%lld",&n,&k);
	for (ll i=1;i<=k;i++)
		dp[i]=k,sum[i]=sum[i-1]+dp[i];
	for (ll i=k+1;i<=n;i++)
		dp[i]=(sum[i-1]-sum[i-k-1])/k +1,sum[i]=sum[i-1]+dp[i];
	printf("%.10Lf\n",dp[n]);
	return 0;
}

C

2014年3月13日到2023年1月24日0时
要比较快手算的话：先把日月全换算成日，由于1.24-3.13为负，我是习惯先提个1年出来
365+24-31-28-13=317；
剩下的年22-14=8，考虑闰年大一，闰年定义（能被4整除不能被100整除||能被400整除），有2016和202两年，所以8*365+2=2922；
加一下=3239；
所以直接输出；
（当然你直接EXCEL复制进去减一下更快，不禁用的）

点击查看代码

#include <bits/stdc++.h>
using namespace std;

int main()
{
	printf("3239\n");
	return 0;
}

D

10^-18用double时SPJ会判错，sqrt求的话也不行，如果你是AC83%，大概就是精度问题
xlgg讲的sqrt内置类型是double的，而sqrtl是long double的，这题需要long double
（又食一个小芝士点）x l g g (/≥▽≤/)

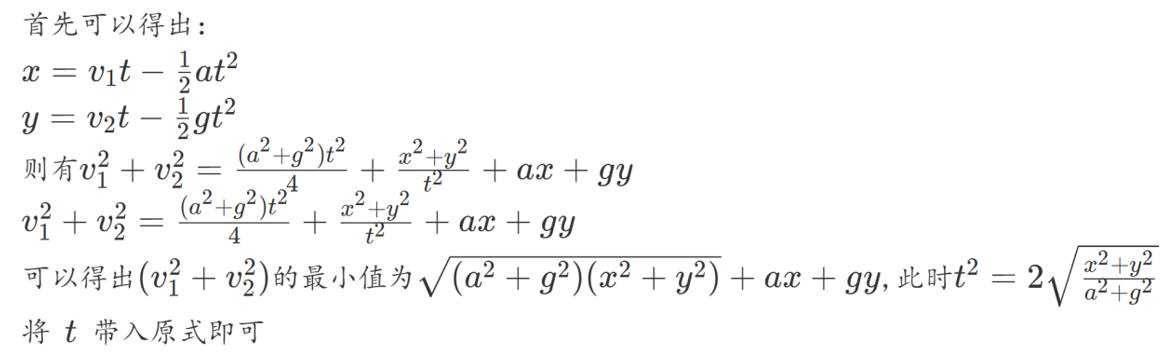
实验室的官方题解：

点击查看代码

#include <bits/stdc++.h>
#define ll long long
#define Ma 1000005
#define inf 1e18
#define mod 1000000007
#define ld long double
using namespace std;
ld x,h,a;


void sol()
{
	scanf("%Lf%Lf%Lf",&x,&h,&a);
	if (sqrtl((x*x+h*h)*(a*a+100))+a*x+10*h>=1e6)
	{
		printf("-1\n");
		return;
	}
	ld t=powl(4*(x*x+h*h)/(100+a*a),1.0/4);
	ld v1=x/t+a*t/2.0,v2=h/t+5.0*t;
	printf("%.18Lf %.18Lf\n",v1,v2);
	return;
}

int main()
{
	ll tt;
	scanf("%lld",&tt);
	while (tt--)
		sol();
	return 0;
}

E

（可能不会更了）

F

简化题目：求\(S_N\) = \(\frac{(1.5)^N}{(2)^{k}}\),\(S_1\)=1.5,求\(S_N\)(k的值取决于N);
不难发现，不管你在什么时候整除二，最后得到的数一定是唯一的，并且在（1，2）区间的数，下面是证明：
若1<\(S_i\)<2,则1.5<\(S_{i+1}\)=\(S_i\)*1.5<3;
若\(S_{i+1}\)在（1，2）之内，则不变。若在（2，3）之内，则除二变为（1，1.5）的数。
那么既然值唯一，那么N是我们给定输入的数，在区间（1，2）内，k也仅有唯一值，我们只需要一直除2就可以得到答案；
解1：快速幂
实验室的官方题解：

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
double qpow(double a, ll b) 
{
	double res = 1;
	while (b) 
	{
		if (b & 1) 
		{
			res = res * a ;
			if (res > 2) res /= 2;
		}
		a = a * a;
		if (a > 2) a /= 2;
		b >>= 1;
	}
	return res;
}
void solve() 
{
	ll n;
	scanf("%lld", &n);
	double res = qpow(1.5, n);
	printf("%.6lf\n", res);
	return ;
}
int main() 
{
	ll t;
	scanf("%lld", &t);
	while (t--) solve();
}

解2：分块（思路）
如果用传统的相乘1.51.5···，这道题必定TLE了。
在n知道的基础下，我们可以一次走2步，即1.5*1.5，或者三步甚至更多，就降低了时间复杂度。

G

首先我们来梳理一下思路（贪心），再来整代码
猫猫可以使用magicpower让一个字符变换为任意字符，结论1：在四个角选择变化会使结果（三角形面积）最大；
结论1证明：三角形任选2个点成一对，如果是平着或竖着，那么变换的点总在四个角上（高相同）；如果是斜着的，那么以它为底，垂直它（即对角线）必定是最大值，在四个角选择是大于等于对角线的值的；
证毕；
结论2：在知道三角形各个坐标情况下，三角形的面积S=(\(x_1\)\(y_2\)-\(x_1\)\(y_3\)+\(x_2\)\(y_3\)-\(x_2\)\(y_1\)+\(x_3\)\(y_1\)-\(x_2\)\(y_2\))
证明：

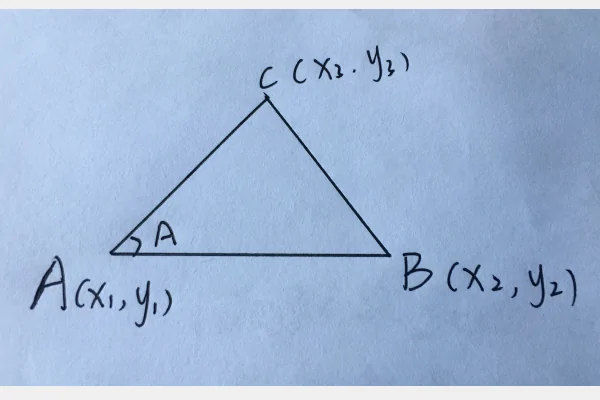
利用向量解决|a·b|=|a|·|b|·|cosA|

点击查看代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
char ch[100][100];
int zf[27];
int max(int a, int b)
{
    return a > b ? a : b;
}
int area(int x1, int y1, int x2, int y2, int x3, int y3)
{
    int ans = abs(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2));
    return ans;
}
int main()
{
    int m, n;
    scanf("%d%d", &m, &n);
    for (int i = 0; i < m; i++)
        scanf("%s", ch[i]);
    for(int i=0;i<m;i++)
    {
        for(int j=0;j<n;j++)
        if(zf[ch[i][j]-'a']==0) zf[ch[i][j]-'a']=1;
    }

    int ans=0;
    for(int h=0;h<=25;h++)
    {
        if(zf[h]==1)
        {
            for(int i=0;i<m;i++)
            {
                for(int j=0;j<n;j++)
                {
                    int ans_i=i,ans_j=j;
                    for(int p=ans_i;p<m;p++)
                    {
                        for(int q=ans_j;q<n;q++)
                        {
                            if(p==ans_i&&q==ans_j) continue;
                            if(ch[p][q]==ch[i][j])
                            {
                                ans=max(ans,area(0,0,i,j,p,q));
                                ans=max(ans,area(0,n-1,i,j,p,q));
                                ans=max(ans,area(m-1,0,i,j,p,q));
                                ans=max(ans,area(m-1,n-1,i,j,p,q));
                            }
                        }
                    }
                }

            }
        }
    }
    printf("%d\n", ans);
    return 0;
}

H

（可能不会更了）

I

防AK题，不会

J

猫猫贴贴

点击查看代码

#include<bits/stdc++.h>
int main() 
{
    puts ( "maomaotietie!" );
} 

K

没学过筛，不会，下一道（可能不会更了）