浙江理工大学2023acm队淘汰赛
浙江理工大学2023淘汰赛部分题目的理解
这里仅提供代码及思路,网站链接如下:
链接>http://47.96.116.66/contest.php?cid=5372<
难度梯度:A B C L D E F K I G H——/) /)
有错误的话请联系我,我也想知道 ฅ(• - •)ฅ
痛!请勿在比赛中使用endl(虽然我不会)
.__ ________ ____________
_____| |__ _____ ____ ___.__.\_____ \/_ \_____ \
/ ___/ | \\__ \ / < | | / ____/ | |/ ____/
\___ \| Y \/ __ \| | \___ |/ \ | / \
/____ >___| (____ /___| / ____|\_______ \|___\_______ \
\/ \/ \/ \/\/ \/ \/
问题 A: ACMer猫猫
题面:
你说的对,但是ICPC是由ACM自主研发的一款全新开放世界冒险游戏。游戏发生在一个被称作PTA的幻想世界,在这里,你将扮演一位名为ACMer的神秘角色,在自由的旅行中邂逅性格各异、能力独特的同伴们, 和他们一起击败强敌,找回失散的亲人——同时,逐步发掘PTA的真相。
刚刚成为成为ACMer的猫猫获得了一个由 A, C, M三个字符组成的字符串,它想知道有多少个长度为3的 ACM子串。
思想:枚举
代码:
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const int N = 1e5 + 10,maxn = 1e6 + 10;
char a[maxn];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
int res=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(i>=3&&a[i-2]=='A'&&a[i-1]=='C'&&a[i]=='M')
{
res++;
}
}
cout<<res;
}
问题 B: 猫猫本
题面:
猫猫在《猫猫本》上写了n个由2个小写字母组成的字符串。现在猫猫想知道每写一个新的字符串后,《猫猫本》上有多少字符串和新添加的字符串是相似的。猫猫认为,当且仅当只有一个位置相同两个字符串是相似的。例如aa和ab,ab和cb是相似的;但是aa和aa,aa和cc是不相似的。
思想:容斥\哈希\map
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const int N = 1e5 + 10,maxn = 1e6 + 10;
int a[N],b[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
for(int i = 1;i <= n; i++){
string s;
cin>>s;
int t1=s[0]-'a'+1;
int t2=s[1]-'a'+1;
cout<<a[t1]+b[t2]-2*b[t1*131+t2]<<"\n";
a[t1]++;
b[t2]++;
b[t1*131+t2]++;
}
return 0;
}
问题 C: 猫猫game
题面:
猫猫一个人在实验室玩游戏。
游戏规则是这样的:每轮游戏会给猫猫两个整数 n,m,猫猫在区间 [1,n] 内,随机取m个整数。该操作进行\(2023^{2023}\)次。如果每次这m个数中,一定存在一个整数是另一个整数的倍数,则猫猫回答Yes,否则回答No。请你告诉猫猫每轮游戏的结果。
思想:鸽巢原理,真的不是找质数(赛时我在干这个蠢事)
样本大至正无穷,相当于取遍样本。下面解释为什么找质数是错误的,注意到《每个》,若n=10,取56789;这时候质数是2357,显然前面的数字更多更符合题意。其次,当n比较大时,一个数的质数个数是\(\frac{X}{lnX}\)级别的,而一个数的一半是\(\frac{X}{2}\)。显然前者小于后者。
下面证正确思想:m>(n+1)/2。每次取一半的时候都是满足题意的,n为偶数时是不影响的,n为奇数时变成n+1(自己理解下吧)
代码:
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const int N = 1e5 + 10,maxn = 1e6 + 10;
void solve(){
int n,m;
cin>>n>>m;
if(m>(n+1)/2){
puts("Yes");
} else {
puts("No");
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while( t-- ){
solve();
}
return 0;
}
问题 D: 猫猫mex
题面:
猫猫一个人在实验室玩游戏。游戏规则是这样的:每轮游戏会给猫猫两个整数\(n,m\),猫猫在区间\([1,n]\)内,随机取m个整数。该操作进行\(2023^{2023}\)次,如果每次这m个数中,一定存在一个整数是另一个整数的倍数,则猫猫回答\(Yes\),否则回答\(No\)。请你告诉猫猫每轮游戏的结果。
输入格式:
第一行一个整数T(\(1\le T\le10^4\)) 表示测试数据个数。
接下来\(T\)行,每行2个整数\(n,m\)(\(4\le n\le 10^5\),\(2\le m\le n\))。
思想:思维,set/线段树/分块
C++中set是有序的,不妨我们设置一个全局U,涵盖所有的数。
添加一个数=在U中删除一个数
删除=添加
这样我们的begin()一定是所求。
代码:
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const int N = 1e5 + 10,maxn = 1e6 + 10;
set<int>s;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int q,op,x;
cin >> q;
for(int i=0;i<N;i++){
s.insert(i);
}
for(int i=1;i<=q;i++){
cin>>op;
if(op==1){
cin>>x;
s.erase(x);
}
if(op==2){
cin>>x;
s.insert(x);
}
if(op==3){
cout<<*s.begin()<<"\n";
}
}
return 0;
}
问题 E: 猫猫sort
题面:
猫猫有一个升序数组,数组中元素两两不同。但是邪恶的paopaooux把他的数组打乱了,猫猫每次可以选择两个元素并交换他们在数组中的位置。
现在猫猫想知道自己最少多少次操作可以重新使数组升序。
思想: 离散化、贪心/置换环
解释已经放代码
代码:
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const int N = 2e5 + 10,maxn = 1e6 + 10;
map<LL,int> mp;
LL num[N],a[N],ans;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
LL n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>num[i];
mp[num[i]]=i;
a[i]=num[i];//a[i]为值,mp[a[i]]为下标
}
sort(a+1,a+n+1);//仅对值排序
// 1 -1 -4 5 4
//-4 -1 1 4 5 排序后
for(int i=1;i<=n;i++)
{
if(num[i] == a[i]) continue;//不需要
LL x=mp[a[i]];//置换,找出a[i]的原位置,例如i=1,a[i]=-4,x=3,y=-4;
swap(num[x],num[i]);//将原数组下标x,i置换
mp[a[i]]=i;
mp[num[x]]=x;//原数组下标置换
ans++;
}
cout<<ans;
return 0;
}
问题 F: 猫猫旅行
题面:
猫猫生活的国家有n个城市,城市从 1~n 编号,城市之间通过公路连接。这个国家有一个奇怪的规定:进入城市需要持有k天内办理的通行证,并且国家的每个城市都可以重新办理新的通行证。现在,猫猫有q个旅行计划,每个旅行计划从u城市出发,到达v城市。请你告诉猫猫每个旅行计划是否可行。
保证整个国家连通,且不存在重复公路。
输入:
第一行三个整数n,m,k,q (2≤n≤2×105,n-1≤m ≤ min(n(n-1)/2,2×105),1≤k≤109,1≤q≤2×105),分别表示表示城市数,公路数,通行证的有效期以及旅行计划个数。
接下来m行,每行三个整数u,v,w(1≤u,v≤n且u≠v,1≤w≤109),表示城市u,v之间有一条公路连接,猫猫通过这条公路需要花费w天。
接下来q行,每行两个整数u,v(1≤ u,v≤n),表示猫猫每个旅行计划的起点与终点。
输出:
q行,如果旅行计划可行,输出Yes;否则输出No。
思想:并查集(不是最短路)
一个简单的并查集,可是赛时的蒟蒻我并没看见。
代码:
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const int N = 2e5 + 10,maxn = 1e6 + 10;
int p[N];
int find(int x)
{
if(p[x]!=x)
{
p[x]=find(p[x]);
}
return p[x];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int m,n,k,q;
cin>>n>>m>>k>>q;
for(int i=1;i<=n;i++)
{
p[i]=i;
}
for(int i=1;i<=m;i++)
{
int u,v,w;
cin>>u>>v>>w;
if(w>k){
continue;
}
u=find(u);
v=find(v);
if(u!=v){
p[u]=v;
}
}
for(int i=1;i<=q;i++)
{
int u,v;
cin>>u>>v;
if(find(u)==find(v))
{
cout<<"Yes\n";
}
else
{
cout<<"No\n";
}
}
return 0;
}
问题 G: 猫猫卡牌
题面:
猫猫与小石头在实验室玩比大小的游戏。
实验室有n张卡牌,编号为1~n。游戏有两种规则:
规则一:先手的玩家从牌堆中抽出一张,后手的玩家从牌堆中抽出一张,然后双方把牌放回牌堆。
规则二:先手的玩家从牌堆中抽出一张后立刻放回牌堆,然后后手的玩家也从牌堆中抽出一张后立刻放回。
无论哪种规则,编号大的一方获胜。如果编号相同,则该轮游戏平局。游戏共进行m轮。在游戏开始前,他们会通过抛硬币的方式决定接下来的m轮游戏谁先手。如果硬币为正面,则猫猫先手;为反面则小石头先手。现在猫猫想知道,在规则一或规则二的情况下,自己至少赢k把的概率。
猫猫不喜欢浮点数,因此它想知道这两个答案对 1000000007 取模的结果:即设答案化为最简分式后的形式为a/b (其中gcd(a,b)=1),输出整数 x 使得 bx≡a (mod 1000000007) 且 0≤ x<1000000007(可以证明这样的整数 x 是唯一的)。
输入
第一行三个整数n,m,k(2≤n≤109,1≤ m≤106,0≤ k≤m),分别表示卡牌的数量,游戏的轮数和猫猫至少赢的轮数。
第二行一个整数x(0≤x≤1),如果x为1,表示硬币为正面;如果x为0,表示硬币为反面。
输出
两行,第一行输出在规则一的情况下猫猫至少赢k把的概率;第二行输出在规则二的情况下猫猫至少赢k把的概率。
思想:数学,概率,逆元
1.首先一眼逆元(计qmi(x,mod-2,mod)为x的逆元),a/b=x,所以a*(b的逆元)为所求
2.规则1:不难发现就是在牌堆中任选两张(不可能重合),一半一半,猫猫赢一把概率是\(\frac{1}{2}\)
3.规则2:转化为规则1,不过多了重合的情况。所有样本是\(\frac{1}{n}*\frac{1}{n}\),为了不重合,在n中任选2张不同即可满足(相当于2的牌映射到1上),为\(C(n,2)\),由于算一个人的概率,即除2,变成\(\frac{\frac{C(n,2)}{2}}{n^2}=\frac{n-1}{2n}\)
4.至少赢k把的概率为赢i(i>=k)的概率相加(题目符合二项分布,高中公式)
代码:
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const LL N = 5e6 + 10,maxn = 1e6 + 10,mod = 1e9 + 7;
LL fact[N], infact[N];
LL qmi(LL a,LL b)
{
LL res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
void init()
{
fact[0]=infact[0]=1;
for(LL i=1;i<maxn;i++)
{
fact[i]=fact[i-1]*i%mod;
infact[i]=infact[i-1]*qmi(i,mod-2)%mod;
}
}
LL C(LL a,LL b)
{
return fact[a] * infact[b] % mod * infact[a-b] % mod;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
init();
LL x,m,n,k;
cin>>n>>m>>k>>x;
LL p1=qmi(2,mod-2),p2=(n-1)*qmi(2*n%mod,mod-2)%mod;
LL res1=0,res2=0;
for(LL i=k;i<=m;i++)
{
res1=(res1+qmi(p1,i)*qmi(1+mod-p1,m-i)%mod *C(m,i)%mod)%mod;
res2=(res2+qmi(p2,i)*qmi(1+mod-p2,m-i)%mod *C(m,i)%mod) % mod;
}
cout<<res1<<"\n"<<res2<<"\n";
return 0;
}
问题 I: 猫猫区间
题面:
猫猫有一个整数x,与一个正整数区间[L,R]。现在猫猫想把这个区间的整数染色,但是猫猫不喜欢与x互质的数,所以这些数不会被染色。请你告诉猫猫可以染色的整数有多少个。
输入:
一行,三个整数L,R,x(1≤L≤R≤10^(18),1≤x≤1012)。
输出:
输出一个整数,表示可以染色的整数个数。
思想:容斥
1.类似于前缀和:[L,R]中被x互质的数同样是[1,R]-[1,L-1]中的数
2.类似于x=6,质因数为2,3.所以在遍历[1,N]的时候2,3的倍数都不会与x互质,但是2*3=6会算上两次,这时候需要减去。
那如果质因数很多时,我们该如何取选取呢?
——————————————用二进制枚举每个数。
代码:
点击查看代码
#include <bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const LL N = 1e5 + 10,maxn = 2e6 + 10,mod = 1e9 + 7;
LL js(LL n,LL x)
{
vector<LL> v;
for(LL i=2;i<=x/i;i++)
{
if(x%i==0)
{
v.push_back(i);
while(x%i==0)
{
x/=i;
}
}
}
if(x>1) v.push_back(x);
LL res=0;
for(LL i=1;i<(1 << v.size() );i++)
{
LL cur=1;
LL cnt=0;
for(LL j=0;j<v.size();j++)
{
if(i >> j & 1)
{
cur*=v[j];
cnt++;
}
}
if(cnt&1)
{
res+=n/cur;
}
else
{
res-=n/cur;
}
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
LL l,r,x;
cin>>l>>r>>x;
LL res=js(r,x)-js(l-1,x);
cout<<res<<"\n";
return 0;
}
问题 K: 猫猫与甜品
题面:
猫猫在实验室吃甜品喽!
猫猫有n个甜品,每个甜品可以给猫猫带来a的快乐值与b的健康值。初始猫猫快乐值和健康值都为0,猫猫不会让自己的健康值为负数,猫猫想知道自己以合理的顺序吃这些甜品(可以不吃完),猫猫的最大快乐值是多少。
输入:第一行一个整数n(1≤n≤500),表示甜品的数量。
接下来n行,每行2个整数ai,bi(1≤i≤n,-100≤ ai,bi≤100),表示第i个甜品的快乐值与健康值。
输出:
输出一个整数,表示猫猫的最大快乐值。
思想:01背包
代码:
点击查看代码
问题 L: 猫猫序
题面;
我们都知道
树的dfs序是一棵树从根节点出发,dfs遍历时依次经过的节点序列。
现在猫猫有一棵包含n个结点的有根树,结点从1~n编号,1号点为根节点。猫猫想让你告诉它,这棵树的dfs序有多少种。
由于答案很大,你需要对998244353取模。
输入:
我们都知道
树的dfs序是一棵树从根节点出发,dfs遍历时依次经过的节点序列。
现在猫猫有一棵包含n个结点的有根树,结点从1~n编号,1号点为根节点。猫猫想让你告诉它,这棵树的dfs序有多少种。
由于答案很大,你需要对998244353取模。
输出:
输出一个整数,表示这棵树dfs序的个数。
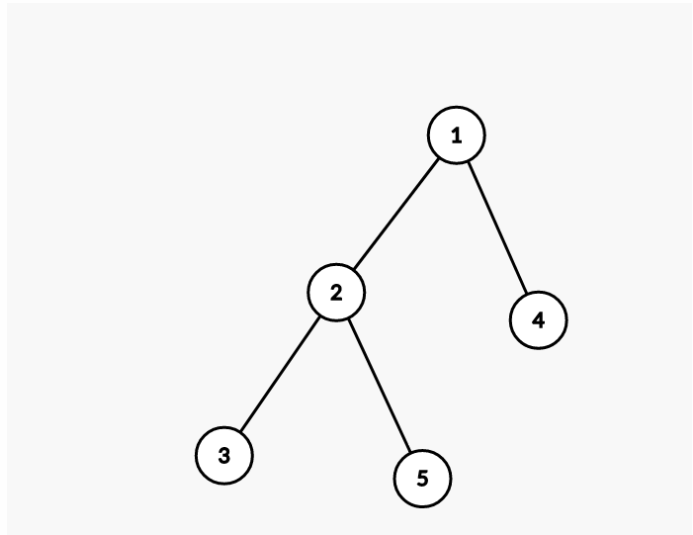
思想:也许是树形dp
1.例如节点1, 2、4为1的子节点,1的dfs序是由2,4构成,2,4分别独立,计算1时需要2*4(应该看的懂吧,我讲的比较抽象)
代码:翁教
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 2e5 + 10, mod = 998244353;
vector<ll>g[N];
ll fact[N], f[N];
void init() {
fact[0] = 1;
for (ll i = 1; i < N; i++) {
fact[i] = fact[i - 1] * i % mod;
}
}
void dfs(ll u, ll fa) {
f[u] = 1;//记得初始化
for (auto v : g[u])
{
if (v == fa)
{
continue;
}
dfs(v, u);//遍历子节点的子节点
f[u] = f[u] * f[v] % mod;
}
f[u] = f[u] * fact[g[u].size() - 1] % mod;//这里因为时子节点的个数,需要-1(这个父节点)
}
int main() {
// freopen("8.in", "r", stdin);
// freopen("8.out", "w", stdout);
init();
ll n;
scanf("%lld", &n);
for (ll i = 1, u, v; i < n; i++) {
scanf("%lld%lld", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
g[1].push_back(-1);
dfs(1, -1);
printf("%lld\n", f[1]);
}
问题 M: 猫猫的位运算
题面:
猫猫有a,b两个整数,想计算出 a&b,a|b,a⊕b 的值,猫猫很快就算出a&b和a|b的值,还没来及的验证是否正确。但是猫猫太困了,很快它就睡着了,醒来后发现原来的a,b两个整数被邪恶的paopaooux擦除掉了。你可以告诉猫猫a⊕b的值或者告诉猫猫算错了。
输入:
第一行一个整数T(1≤T≤105) ,表示测试数据个数。
接下来T行,每行两个整数x,y(1≤ x,y≤109),分别表示a&b,a|b的值。
输出:
T行,每行一个整数,表示a⊕b的值。若a⊕b不存在则输出-1。
思想:
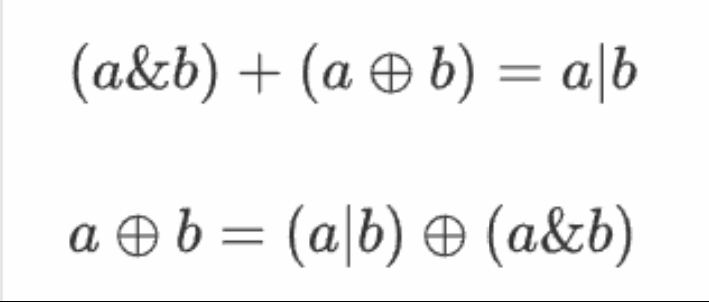
tips:<&> 有0出0,全1出1 ------------ <|> 有1出1,全0出0
其实自己可以推的:
对于a&b,a|b,用二进制表示,例如2,5分别为10,101
这时候发生了矛盾:因为10中的“1”表示ab二进制第二位全是1(与为1),同时101中“0”表示ab二进制第二位全为0(或为0)
代码
点击查看代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
#pragma GCC optimize(2)
typedef long long LL;
using namespace std;
const int N = 1e5 + 10,maxn = 1e6 + 10;
void solve()
{
int x, y;
cin>>x>>y;
if (y-x!=(x^y))
{
cout<<-1<<"\n";
}
else
{
int h=x^y;
cout<<h<<"\n";
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while (t--)
{
solve();
}
return 0;
}
本文来自博客园,作者:shany212,转载请注明原文链接:https://www.cnblogs.com/codeshany/p/zstu_2023tts.html


