Catalan number-神奇的卡特兰数

卡特兰数介绍

简介

首先我们来了解一下什么是卡特兰数
从零开始，卡特兰数的前几项为1,1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845······

式子

首先它满足\(C_{n+1}=C_{0}C_{n-1}+C_1C_{n-1}+...+C_nC_0\)

通项公式：

\(f_n=\frac{1}{n+1}C_{2n}^n\)
实际上与\(f_n=C_{2n}^n-C_{2n}^{n-1}\)一摸一样

样例

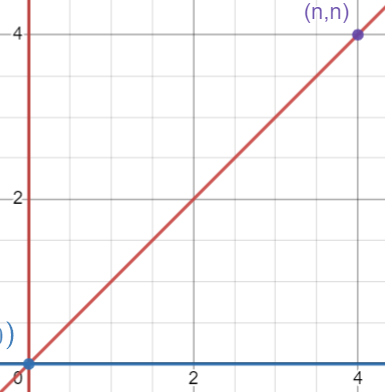
从（0，0）走到（n，n），条件：每次只能往上或往后走一格，且向右次数不小于向上次数。问有几条路径？

解释

简便解释：合理数=总数-非法数；
总数：我们从（0，0）走到（n，n）必须走2n步，其中n步向上、n步向右。我们的总数就是在2n中取n步向右，及\(C_{2n}^n\)
非法数：见图

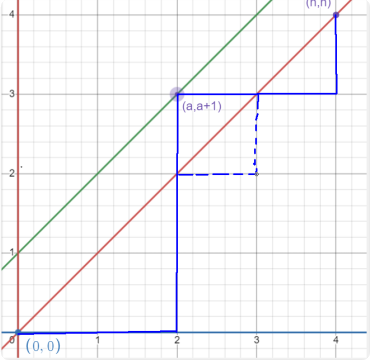
对某一条路径若碰到了y=x+1，次数向上次数已经大于向右次数了，已经错了，但是每一条错误的路径都是可以通过对y=x的对称来得到一条正确的路径。因此（n,n）关于y=x+1
对称点是（n-1，n+1），到的总数仍然为（n-1+n+1）=2n，但是向右为n-1，所以非法数为\(C_{2n}^{n-1}\)
所以得到合理数\(f_n=C_{2n}^n-C_{2n}^{n-1}\)
我们改变一下，如果是走到（n，m）呢？再加上\(N_r\)减\(N_h\)(向右的步数-向上的步数)>=k？（在题目有解情况下）
不难发现，我们会将y=x+1下移k变为y=x+1-k；此时对称点为（n+k-1，1+m-k）
此时合法数为\(f_n=C_{n+m}^{n}-C_{n+m}^{n-k-1}\)

题目转化

题目一：01序列

你现在有n个0和n个1，问有多少个长度为2n的序列，使得序列的任意一个前缀中1的个数都大于等于0的个数
例如 1010、1100都是合法的
而 0101、0110、1001、0011都不合法
设1为右，0为上，是不是和我们的样例一摸一样。

题目二：括号匹配

题目：你有n个左括号，n个右括号，问有多少个长度为2n的括号序列使得所有的括号是合法的？

（）（）是合法的，因为前缀中左括号的个数必须大于右括号的个数
左括号为1，右括号为0
使得前缀之中使得序列的任意一个前缀中1的个数都大于等于0的个数，这就转化成题目一了

题目三：列车调度

题目如下：

点击查看代码

题目：其中，A为入口，B为出口，S为中转盲端。所有铁道均为单轨单向式：列车行驶的方向只能是从A到S，再从S到B；另外，不允许超车。因为车厢可在S中驻留，所以它们从B端驶出的次序，可能与从A端驶入的次序不同。不过S的容量有限，同时驻留的车厢不得超过m节。
设某列车由编号依次为{1, 2, ..., n}的n节车厢组成。调度员希望知道，按照以上交通规则，这些车厢能否以{a1, a2, ..., an}的次序，重新排列后从B端驶出。如果可行，应该以怎样
的次序操作?

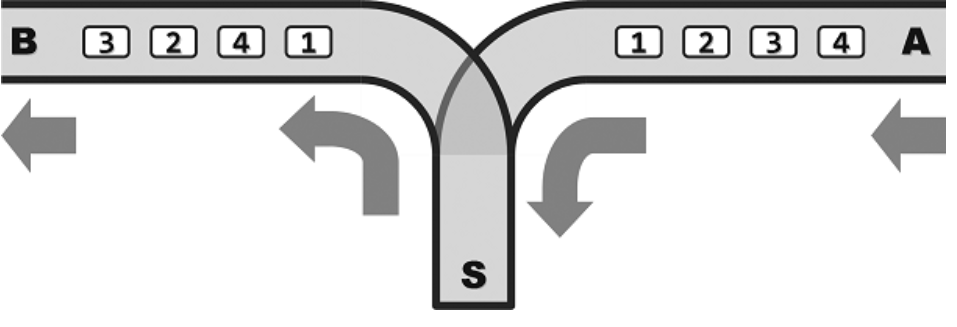
若m=2就等效为312问题，同时也是进栈出栈的问题，那m=3呢？

题目四：不相交弦

题目

圆周上有N个点。连接任意多条不相交的弦（共用端点也算相交）共有多少种方案？由于结果可能很大，你只需要输出这个答案mod 12345的值。

点击查看代码

#include<bits/stdc++.h>
#define N 100010
using namespace std;
int f[N];
int n;
int main()
{
	memset(f, 0, sizeof(f));
	scanf("%d", &n);
	f[0] = 1；
        f[1] = 1; 
        f[2] = 2;
	for(int i = 3; i <= n; ++i)
        {
		f[i] = f[i - 1];
		for(int j = 0; j <= i - 2; ++j)
                {
			f[i] += f[j] * f[i - 2 - j];
			f[i] %= 12345;
		}
	}
	printf("%d\n", f[n]);
	return 0;
}

一个点只能有两个状态，要么连线，要么不连；所以让新加入的这个点和所有边连线，能将图分成两个部分，所以此时的方案数就是两个部分的累计和；还有一种情况是这个点不和任何点相连，所以要单独加上f[i - 1]；

题目五：二叉树构成

题目：n个结点下，可构成多少种不同形态的二叉树？

当结点个数为n时，首先抽出一个结点作为根结点，则剩余结点个数为n-1。
当左分支上结点个数为0时，右分支上结点个数为n-1
当左分支上结点个数为1时，右分支上结点个数为n-2
当左分支上结点个数为2时，右分支上结点个数为n-3
…右边同理
所以它满足\(C_{n+1}=C_{0}C_{n-1}+C_1C_{n-1}+...+C_nC_0\)
化为组合数为：\(f_n=\frac{C_{2n}^{n}}{n+1}\)

题目六：凸多边形的划分

一个凸的n边形，用直线连接他的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案？
原理：n边形里一条基边与任意两个不相邻的顶点相连（相当于中间画了一个三角形），把n边形变成变成分别k，n-k+1边形（2<k<n）
与上一题子树一模一样了，注意的是由于\(f_2\)没有规定，但是计算时需要\(f_2\)，因此我们将其定为1，相乘的时候是不影响式子的结果的（错的的话求求正解QWQ，轻喷）
如果你理解成\(E_{5}=E_{3}E_{4}+E_4E_{3}\)，那么你只考虑了一条边，并且有重复也没有减去。
塞格纳（Johann Andreas Segner）的公式（其中规定E2=1）：
\(E_{n}=E_{2}E_{n-1}+E_1E_{n-1}+...+E_{n-1}E_2\)

点击查看代码

#include<iostream>

using namespace std;

unsigned long long f[40]={0};

int main()
{
      int n;
      cin>>n;   
      f[2]=1,f[3]=1,f[4]=2;
      for(int i=5;i<=n;i++)
      {
       	  for(int k=2;k<i;k++)
    	  {
    		f[i]+=f[k]*f[i-k+1]、、
	  }
      }
	   cout<<f[n];
	return 0;
}

题目七：两列排队

12个高矮不同的人，排成两排，每排必须是从矮到高排列，而且第二排比对应的第一排的人高，问排列方式有多少种？
这个也是一个卡特兰数的问题，隐藏的很深。
首先我们默认12个人先从矮到高站成一列
我们将在第一列为0，第二列为1
那么例如 0 0 0 0 1 1 0 1 0 1 1 1 是合法的
如果一个排序中出现前缀中1比0多的情况，例如1 1 1 0 0 1 0 1 0 1 0 0，那么后出现的0站在第一排时就会比第二排高，所以无法达成对应关系
那这样是不是转化为01了。

题目八：包装信封（递推）

有n个信封，包含n封信，现在把信拿出来再装回去，要求每封信不能装回它原来的信封，问有多少种装法？
设第n中装法为\(f_n\)
假设第n封信放入了第i封信，分为两种情况
1.第i封信也放入了第n封信中，那么剩下的选择有\(f_{n-2}\)种
2.第i封信未放入了第n封信中，那么剩下的选择有\(f_{n-1}\)种
i！=n，所以i的选择有（n-1）种
所以\(f_{n}=（n-1）*（f_{n-1}+f_{n-2}）\)