神经网络与深度学习 邱锡鹏 第4章 前馈神经网络 读书笔记
人工神经网络是指一系列受生物学和神经科学启发的数学模型。在本章中，主要关注采用误差反向传播来进行学习的神经网络，即作为一种机器学习模型的神经网络。从机器学习的角度来看，神经网络一般可以看作是一个非线性模型，其基本组成单元为具有非线性激活函数的神经元，通过大量神经元之间的连接，使得神经网络成为一种高度非线性的模型。神经元之间的连接权重就是需要学习的参数，可以在机器学习的框架下通过梯度下降方法来进行学习。
4.1 神经元
人工神经元，简称神经元，是构成神经网络的基本单元，其主要是模拟生物神经元的结构和特性，接受一组输入信号并产生输出。
假设一个神经元接收D个输入x1,x2,....,xD,令向量 x = [x1;x2;...;xD]来表示这组输入，并用净输入 z ∈ R表示一个神经元所获得的输入信号x的加权和，
其中w = [w1;w2;...;wD]∈RD是D维的权重向量，b ∈ R是偏置。
净输入z在经过一个非线性函数f(.)后，得到神经元的活性值a, a = f（z）
其中非线性函数f(.)称为激活函数。
下图给出了一个典型的神经元结构示例。
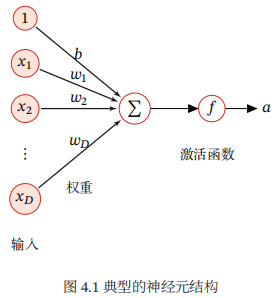
激活函数需要具备以下几点性质：
（1）连续并可导（允许少数点上不可导）的非线性函数，可导的激活函数可以直接利用数值优化的方法来学习网络参数。
（2）激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
（3）激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。
下面介绍几种在神经网络中常用的激活函数。
4.1.1 Sigmoid型函数
Sigmoid型函数是指一类S型曲线函数，为两端饱和函数。常用的Sigmoid型函数有Logistic函数和Tanh函数。
Logistic函数定义：
Logistic函数可以看成是一个”挤压“函数，把一个实数域的输入”挤压“到（0,1）。当输入值在0附近时，Sigmoid型函数近似为线性函数；当输入值靠近两端时，对输入进行抑制。输入越小，越接近0；输入越大，越接近1。
因为Logistic函数的性质，使得装备了Logistic激活函数的神经元具有以下两点性质：（1）其输出直接可以看作是概率分布，使得神经网络可以更好地和统计学习模型进行结合。（2）其可以看作是一个软性门，用来控制其他神经元输出信息的数量。
Tanh函数定义：
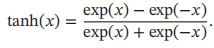
Tanh函数的输出是零中心化的，而Logistic函数的输出恒大于0.非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移，并进一步使得梯度下降的收敛速度变慢。下图是Logistic函数和Tanh函数的形状。
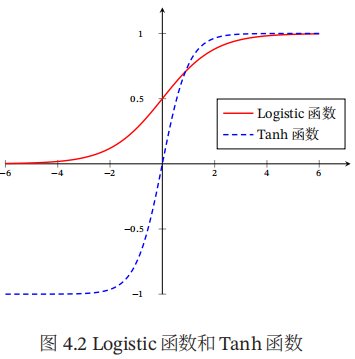
4.1.1.1 Hard-Logistic函数和Hard-Tanh函数
以Logistic函数σ(x)为例，其导数为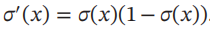
。Logistic函数在0附近的一阶泰勒展开为
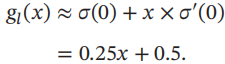
这样Logistic函数可以用分段函数hard-logistic(x)来近似
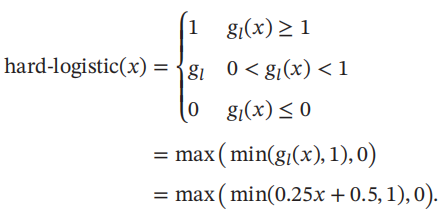
同理，Tanh函数也可以用分段函数hard-tanh(x)来近似
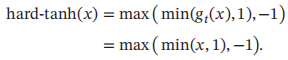
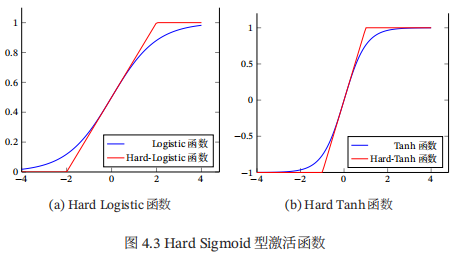
下图给出了Hard-Logistic函数和Hard-Tanh函数的形状
4.1.2 ReLU函数
ReLU函数是目前深度神经网络中经常使用的激活函数，ReLU定义如下：
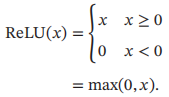
优点：采用ReLU的神经元只需要进行加、乘和比较的操作，计算上更加高效。ReLU函数在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度。
缺点：ReLU函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移，会影响梯度下降的效率。
4.1.2.1 带泄漏的ReLU
带泄漏的ReLU在输入x < 0 时，保持一个很小的梯度λ。这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能被激活。带泄漏的ReLU的定义如下：
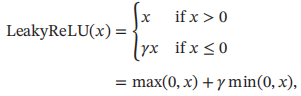
其中r是一个很小的常数，比如0.01。当r <1时，带泄漏的ReLU也可以写为
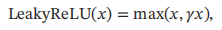
4.1.2.2 带参数的ReLU
带参数的ReLU（Parametric ReLU,PReLU）引入一个可学习的参数，不同神经元可以有不同的参数。对于第i个神经元，其PReLU定义为
4.1.2.3 ELU函数
ELU(指数线性单元)是一个近似的零中心化的非线性函数，其定义为
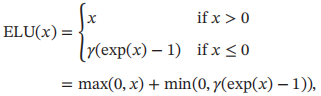
4.1.2.4 Softplus函数
定义如下：
具有单侧抑制、宽兴奋边界的特性，却没有稀疏激活性
下图给出了ReLU、Leaky ReLU、ELU以及Softplus函数的示例
4.1.3 Swish函数
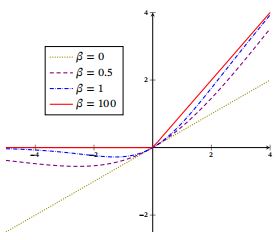
Swish函数是一种自门控激活函数，定义为
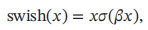
下图给出了Swish函数的示例
4.1.4 高斯误差线性单元
高斯误差线性单元(GELU)和Swish函数比较类似，也是一种通过门控机制来调整其输出值的激活函数。
GELU(x) = xP(X <= x)
其中P(X <= x)是高斯分布的累积分布函数。GELU可以用Tanh函数或Logistic函数来近似。
4.1.5 Maxout单元
Maxout单元也是一种分段线性函数。Sigmoid型函数、ReLU等激活函数的输入是神经元的净输入z,是一个标量。而Maxout单元的输入是上一层神经元的全部原始输出，是一个向量。
每个Maxout单元有K个权重向量wk ∈ RD和偏置bk。对于输入x,可以得到K个净输入zk，1 <= k <= K
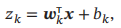
Maxout单元的非线性函数定义为
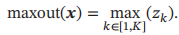
4.2 网络结构
通过一定的连接方式或信息传递方式进行协作的神经元可以看作是一个网络，就是神经网络。
目前常用的神经网络结构有以下三种：
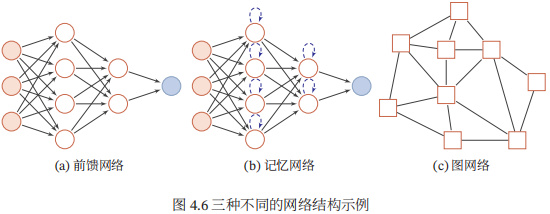
4.2.1前馈网络
前馈网络中各个神经元按接收信息的先后分为不同的组。每一组可以看作一个神经层，每一层中的神经元接受前一层神经元的输出，并输出到下一层神经元。整个网络中的信息是朝一个方向传播，没有反向的信息传播，可以用一个有向无环路图表示。
前馈网络可以看作一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。这种网络结构简单，易于实现。
4.2.2 记忆网络
记忆网络，也称为反馈网络，网络中的神经元不但可以接收其他神经元的信息，也可以接收自己的历史信息。记忆网络包括循环神经网络、Hopfield网络、玻尔兹曼机、受限玻尔兹曼机等。
记忆网络可以看作一个程序，具有更强的计算和记忆能力。
4.2.3 图网络
图网络是定义在图结构数据上的神经网络。图中每个结点都由一个或一组神经元构成。节点之间的连接可以是有向的，也可以是无向的。每个节点可以收到来自相邻节点或自身的信息。
下图给出了前馈网络、记忆网络和图网络的网格结构示例，其中圆形节点表示一个神经元，方形节点表示一组神经元。
4.3 前馈神经网络
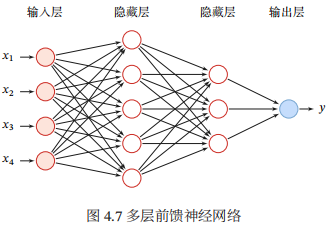
在前馈神经网络中，各神经元分别属于不同的层。每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层称为输入层，最后一层称为输出层，其他中间层称为隐藏层、整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示。下图给出了前馈神经网络的示例。
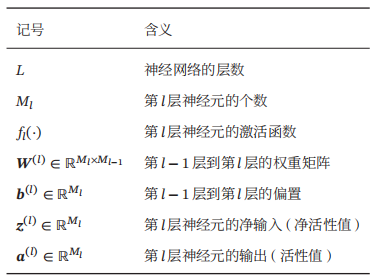
符号定义：
令a(0) = x,前馈神经网络通过不断迭代下面公式进行信息传播：
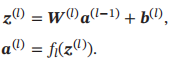
可以合并为以下式子：
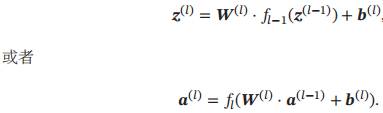
4.3.1 通用近似定理
4.3.2 应用到机器学习
给定一个训练样本(x,y)，先利用多层前馈神经网络将x映射到φ(x)，然后再将φ(x)输入到分类器g(.)
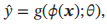
其中g(.)为线性或非线性的分类器，θ为分类器g(.)的参数，y为分类器的输出。
如果分类器g（.）为Logistic回归分类器或Softmax回归分类器，那么g(.)也可以看成是网络的最后一层，即神经网络直接输出不同类别的后验概率。
4.3.3 参数学习
如果采用交叉熵损失函数，对于样本(x,y)，其损失函数为
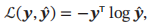
给定训练集D，将每个样本x(n)输入给前馈神经网络，得到网络输出为
,其在数据集D上的结构化风险函数为：
||W||F2是正则化项，用来防止过拟合。这里的||W||F2一般使用Frobenius范数：
网络参数可以通过梯度下降法来进行学习。第l层的参数W(l)和b(l)参数更新方式为
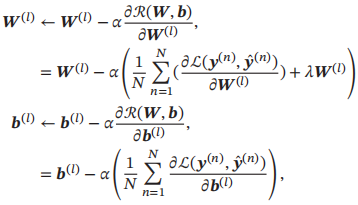
α为学习率。
4.4 反向传播算法
先计算L关于参数矩阵中每个元素的偏导数，根据链式法则，
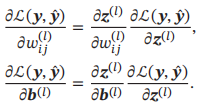
从上式可以看出，第l层的误差项可以通过第l+1层的误差项计算得到，这就是误差的反向传播。
使用误差反向传播算法的前馈神经网络训练可以分为以下三步：
（1）前馈计算每一层的净输入z(l)和激活值a(l)，直到最后一层
（2）反向传播计算每一层的误差项δ (l)
（3）计算每一层参数的偏导数，并更新参数。
4.5 自动梯度计算
因为手动求导并转换为计算机程序的过程非常琐碎并容易出错，导致实现神经网络变得十分低效。实际上，参数的梯度可以让计算机来自动计算。目前，主流的深度学习框架都包含了自动梯度计算的功能，即我们可以只考虑网络结构并用代码实现，其梯度可以自动进行计算，无需人工干预，这样可以大幅提高开发效率。
自动计算梯度的方法可以分为以下三类：数值微分、符号微分和自动微分。
4.5.1 数值微分
数值微分是用数值方法来计算函数f（x）的导数。函数f(x)的点x的导数定义为
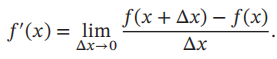
然而在实际应用中，经常使用下面公式来计算梯度，可以减少截断误差。
4.5.2 符号微分
符号微分是一种基于符号计算的自动求导方法。符号计算也叫代数计算，是指用计算机来初六带有变量的数学表达式。
4.5.3 自动微分
自动微分可以直接在原始程序代码进行微分，因此自动微分成为目前大多数深度学习框架的首选。自动微分的基本原理是所有的数值计算可以分解为一些基本操作，包含+，-，×，/和一些初等函数exp,log,sin,cos等，然后利用链式法则来自动计算一个复合函数的梯度。
举例：
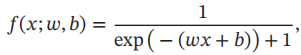
连边上的红色数字表示前向计算时复合函数中每个变量的实际取值。
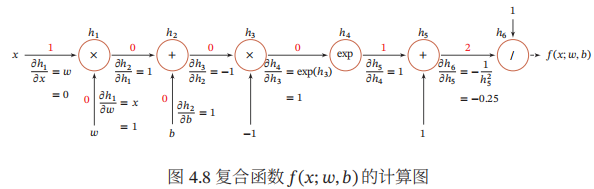
那么
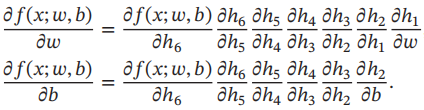
4.6 优化问题
神经网络的参数学习比线性模型更加困难，主要原因有两点：（1）非凸优化问题和（2）梯度消失问题
4.7 总结和深入阅读
